DOI: 10.1590/1089-6891v18e-39566

ZOOTECNIA

MODELOS DE REGRESSÃO ALEATÓRIA PARA CARACTERÍSTICA DE CRESCIMENTO EM BOVINOS DA RAÇA GUZERÁ

RANDOM REGRESSION MODELS FOR GROWTH TRAIT IN GUZERA CATTLE

Jorge Luis Ferreira^1*
Tiago Bresolin²
Fernando Brito Lopes³
José Américo Soares Garcia⁴
Leandro Lopes Nepomuceno¹
Aline Beatriz Schmidt¹
Raysildo Barbosa Lobo⁵

¹Universidade Federal do Tocantins, Araguaína, TO, Brasil
²Faculdade de Ciências Agrárias e Veterinárias da UNESP, Jaboticabal, SP, Brasil
³College of Agricultural & Life Sciences, University of Wisconsin, Madison, Wiscosin, USA.
⁴Universidade de Brasília, Brasília, DF, Brasil.
⁵Associação Nacional de Criadores e Pesquisadores, Ribeirão Preto, SP, Brasil.
^*Autor para correspondência - jlferreira@mail.uft.edu.br

Resumo
O objetivo do presente trabalho foi estimar componentes de (co)variâncias e parâmetros genéticos para características de pesos do nascimento ao sobreano (550 dias de idade) para bovinos da raça Guzerá, por meio de modelos de regressão aleatória. Os dados utilizados são de animais (machos e fêmeas) nascidos entre 1993 e 2011 e pertencentes a dez fazendas de sete estados brasileiros. O modelo de melhor ajuste considerou os efeitos genéticos aditivos diretos e maternos e os de ambiente permanente do animal ajustado usando polinômios ortogonais de Legendre de quarta, terceira e segunda ordem, respectivamente. As maiores estimativas de herdabilidade diretas foram observadas para os pesos ao nascimento (0,88) e ao sobreano (0,70). As correlações genéticas foram de moderada a alta magnitude, mantendo-se elevada mesmo com o aumento da distância entre as idades.
Palavras-chave: bovinos de corte; correlações genéticas; herdabilidade; polinômios ortogonais de Legendre.

Abstract
The aim of this study was to estimate (co)variance components and genetic parameters from birth to yearling weight (550 days of age) in Guzerá cattle, using random regression models. Data set from animals (male and female) born between 1993 and 2011 belonging to ten farms in seven Brazilian States were used. The best-fit model considering direct and maternal genetic effect and permanent environmental animal effect were adjusted by fourth, third, and second order, respectively, using orthogonal polynomials of Legendre. The higher estimated values of direct heritability were observed in birth (0.88) and yearling weight (0.70). The genetic correlations were moderate to high magnitude, remaining up even with the increase in the ages gap.
Key words: beef cattle; genetic correlations; heritability; orthogonal polynomials of Legendre.

Recebido em: 27 janeiro de 2016
Aceito em: 14 dezembro de 2016

Introdução

Os programas de melhoramento genético de bovinos no Brasil têm preconizado a seleção para características de crescimento, como ganho de peso ou pesos calculados para idades-padrão. Essas características são de fácil mensuração e apresentam herdabilidade de moderada a alta magnitude e, portanto, são amplamente utilizadas como critérios de seleção, resultando em maior progresso genético^(1,2). No entanto, algumas características como tamanho corporal ou de crescimento, quando avaliadas no mesmo indivíduo em várias idades, comumente apresentam medidas chamadas de longitudinais^(3,4). Essas medidas normalmente são utilizadas em modelos de características múltiplas, os quais podem ser super parametrizados ao se utilizarem medidas em várias idades. Além disso, a matriz de covariâncias não é estruturada e, para que se possam fazer inferências sobre medidas no tempo, é importante modelar adequadamente a estrutura de covariâncias^(5,6), levando em consideração o efeito temporal que atua e conecta cada mensuração.
Nos últimos anos tem-se proposto a utilização de modelos de regressão aleatória para se analisarem as características observadas várias vezes ao longo da vida do animal^(4,7-8). Medidas longitudinais de peso que se alteram com a idade podem ser representadas por uma trajetória em função do tempo. Assim, um determinando valor em cada uma das possíveis idades, em que registros repetidos da mesma característica e medidos em idades diferentes, passa a representar diferentes características. Tais trajetórias são denominadas de características de “dimensão infinita”^(3,9,10), desenvolvida por meio de um modelo matemático de regressão sobre o tempo, para que se possa estimar parâmetros e funções da curva.
Dessa forma, o objetivo deste estudo foi estimar componentes de (co)variâncias e parâmetros genéticos para peso do nascimento ao sobreano (550 dias de idade), utilizando-se modelos de regressão aleatória com diferentes ordens de ajuste para os efeitos genéticos aditivos diretos e maternos e os de ambiente permanente de animal para bovinos da raça Guzerá.

Materiais e Métodos

Foram utilizadas medidas de peso e idade de bovinos da raça Guzerá, provenientes da Associação Nacional dos Criadores e Pesquisadores – ANCP, mensuradas do nascimento aos 550 dias de idade. Os animais são oriundos de fazendas localizadas nos estados do São Paulo (SP), Mato Grosso do Sul (MS), Mato Grosso (MT), Goiás (GO), Tocantins (TO), Pará (PA) e Rondônia (RO), nascidos entre 1993 e 2011. No conjunto de dados foram mantidos apenas animais com genealogia conhecida e registro de peso com a informação da idade. Foram consideradas três estações de nascimento (janeiro a abril; maio a agosto; setembro a dezembro). Os grupos de contemporâneos (GC) reuniram animais nascidos no mesmo ano e estação, do mesmo sexo, pertencentes à mesma fazenda e criados no mesmo grupo de manejo.
Para a consistência do arquivo de dados (Tabela 1) foram realizadas algumas restrições por meio de rotinas desenvolvidas em linguagem do SAS⁽¹¹⁾, considerando-se apenas animais com mais de três mensurações de peso, GC com mais de quatro animais e touros com mais de três progênies. Além disso, excluíram-se registros de peso fora dos intervalos de mais ou menos três desvios-padrão, dado pela média do GC. A conexidade entre os GC foi observada por meio do software AMC⁽¹²⁾, com base no número total de laços genéticos, considerando-se no mínimo dez laços genéticos.



Para a estimação dos componentes de (co)variâncias foram realizadas análises uni-característica, pelo método da máxima verossimilhança restrita livre de derivadas, através do modelo animal, ajustando-se polinômios ortogonais de Legendre variando de segunda a quarta ordem para modelar os efeitos genéticos aditivos direto e maternos e de ambiente permanente do animal. A não inclusão do efeito de ambiente permanente materno se deve à proporção de apenas 1,6 filhos por vaca. As análises foram realizadas com o software WOMBAT⁽¹³⁾ e o algoritmo AIREML com o critério de convergência padrão menor que 10^-8.
Os modelos consideraram os efeitos aleatórios genéticos aditivos diretos e materno e de ambiente permanente do animal como fixos e o efeito de GC, com as idades do animal à pesagem e da vaca ao parto (efeitos linear e quadrático) como covariáveis. A curva média da população foi modelada considerando-se o polinômio ortogonal de Legendre de quarta ordem e, para agrupar classes de variâncias residuais semelhantes, formaram-se oito classes, de acordo com a idade em dias (1, 2-45, 46-90, 91-140, 141-180, 181-230, 231-320, 321-550).
O modelo geral de regressão aleatória utilizado foi:



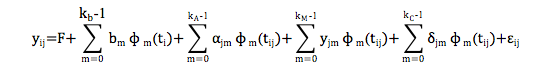
Em que: y_ij é a i^ésima medida referente ao j^ésimo animal; F é o conjunto de efeitos fixos; b_m é o coeficiente de regressão fixo para modelar a curva média da população; ɸ_m (ti) é a função de regressão que descreve a curva média da população de acordo com a idade do animal; ɸ_m (tij) é a função de regressão que descreve as trajetórias de cada indivíduo j, de acordo com a idade (ti), para os efeitos aleatórios genéticos aditivos direto e materno e de ambiente permanente do animal; α_jm, y_jm , δ_jm, são os coeficientes de regressão genéticos aditivos direto e materno e de ambiente permanente de animal, respectivamente, para cada animal; k_b, k_A, k_M e k_C são as ordens dos polinômios a serem ajustados; ε_ij é o erro aleatório associado a cada idade i do animal j. Na forma matricial, o modelo fica expresso como:

y = X_b + Z_1α + Z_2ϒ + W_1δ + ε

Em que: y é o vetor de observações; b é o vetor de efeitos fixos; α é o vetor aleatório dos coeficientes de regressão genéticos aditivos diretos; ϒ é o vetor aleatório dos coeficientes de regressão genéticos maternos; δ é o vetor aleatório dos coeficientes de regressão de ambiente permanente do animal; X, Z₁, Z₂ e W₁ são as matrizes de incidência correspondentes às observações, para efeitos fixos, aleatórios genéticos aditivos direto e materno e de ambiente permanente de animal, respectivamente; ε é o vetor de resíduos.

As pressuposições em relação aos componentes são:

Em que K_A, K_M e K_C são as matrizes de (co)variâncias entre os coeficientes de regressão aleatórios para os efeitos genéticos aditivos direto e materno e de ambiente permanente do animal, respectivamente; A é a matriz de parentesco; I é a matriz identidade; N_a é o número de animais com pesagens; ⨂ é o produto de Kroneker entre matrizes; R é a matriz de variâncias residuais. Para comparar os diferentes modelos de regressão aleatória testados, foram utilizados os critérios de informação de Akaike (AIC = - 2 logL + 2p) e Bayesiano de Schwarz (BIC = - 2 logL + p log (N-r(X))), em que p é o número de parâmetros do modelo; N é o total de observações e r é o posto da matriz X (matriz de incidência para os efeitos fixos). O melhor ajuste do modelo está em função dos menores valores desses critérios. Os AIC e BIC permitem a comparação de modelos não hierárquicos e penalizam modelos mais parametrizados, sendo o BIC mais rigoroso, favorecendo os modelos mais parcimoniosos⁽¹⁴⁾. Valores menores de AIC e BIC indicam melhor ajuste do modelo.

Resultados e Discussão

A menor quantidade de registros para a característica peso foi observada para o período do nascimento (dia um) até os 45 dias (Tabela 1). Por outro lado, foi verificado um aumento na quantidade de informações em idades subsequentes, parte devido ao aumento na amplitude das classes de idades utilizadas. O peso médio dos indivíduos teve um crescimento linear de acordo com a idade. O maior coeficiente de variação foi encontrado para a classe de 2 a 45 dias de idade, permanecendo constantes nas demais classes utilizadas.

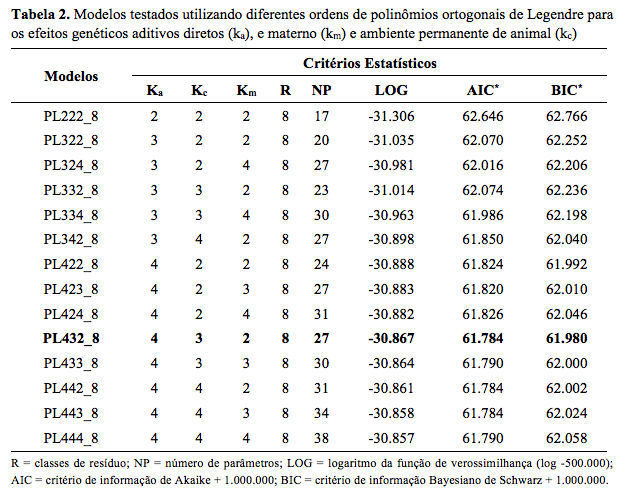
No presente trabalho foram testados 14 modelos com diferentes ordens de ajuste dos polinômios ortogonais de Legendre para os efeitos considerados (Tabela 2). O modelo de melhor ajuste, que apresentou os menores valores para os critérios AIC e BIC, com um total de 27 parâmetros foi o PL432_8. Neste modelo, as variâncias genéticas aditivas direta e materna e de ambiente permanente do animal foram modeladas com polinômios de quarta, terceira e segunda ordem, respectivamente.

As estimativas das variâncias genéticas aditivas diretas aumentaram gradualmente até os 500 dias de idade, sendo que, após esse período, houve aumento acentuado nas estimativas (Figura 1a). Para o ambiente permanente do animal, as variâncias estimadas no presente trabalho aumentaram constantemente até próximo aos 400 dias de idade com ligeira diminuição nas estimativas em idades posteriores (Figura 1b). A estimativa de variância genética aditiva materna aumentou gradualmente de forma linear do nascimento até o final do período estudado, porém menos acentuada quando comparada com a variância genética aditiva direta (Figura 1a). Os resultados encontrados são semelhantes aos descritos por Albuquerque e Meyer⁽¹⁵⁾ para raça Nelore e por Sousa Júnior et al.⁽¹⁶⁾ e Dias et al.⁽¹⁷⁾ para a raça Tabapuã; entretanto, esses autores observaram aumento da variância genética aditiva materna após a desmama dos animais. Os baixos valores de variância genética aditiva materna observados no presente trabalho podem estar associados à estrutura dos dados, na qual aproximadamente 80% das mães possuíam apenas uma progênie. Segundo Ferreira⁽¹⁸⁾, isso é possível, pois estimativas de variância genética aditiva materna são dependentes da proporção de elos mãe-progênie. Assim, quanto maior for essa relação, maiores e mais acuradas são as estimavas de variância genética aditiva materna.

A variância residual aumentou com a idade dos animais, porém, os menores valores foram observados até os 180 dias de idade (Figura 1d). É provável que a menor variância residual estimada no período pré-desmama ocorra devido à homogeneidade de ambiente de criação dos bezerros, fase em que o animal é basicamente dependente do ambiente materno que, embora seja genético para a mãe, é um fator ambiental para o bezerro. Contudo, deve-se considerar a variância em termos de proporção, visto que a ordem de grandeza da variável é dependente da idade do animal. Segundo Dias et al.⁽¹⁷⁾, a ordem de ajuste dos polinômios e a modelagem do resíduo podem interferir na estimação dos componentes de variância. Dessa forma, as estimativas de parâmetros genéticos podem ser influenciadas pelo modelo de regressão adotado e, portanto, a separação dos efeitos aleatórios genéticos e de ambiente permanente em direto e materno deve ser procedida para melhor modelar as mudanças que ocorrem no crescimento de bovinos.

Quando a variância residual é homogênea, assume-se que o ambiente temporário afetou igualmente todas as idades ao longo do crescimento do animal, o que nem sempre ocorre. Além disso, pode ocorrer um aumento da variância de ambiente permanente do animal. Por este motivo, no presente estudo, as variâncias residuais foram modeladas considerando-se oito classes diferentes como relatado por Huisman et al.⁽¹⁴⁾. Os autores reportaram que o mais adequado para ajustar pesos de bovinos ao longo das idades é adotar estruturas heterogêneas de variância residual.

A herdabilidade direta estimada utilizando o modelo de melhor ajuste (PL432_8) reduziu do nascimento até os 45 dias de idade, aumentando após este período (Figura 2, à esquerda). O modelo de regressão aleatória possibilitou estimar as herdabilidades em qualquer idade.

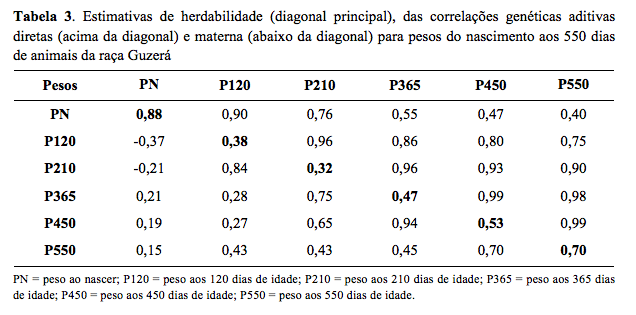
Considerando as idades-padrão (Tabela 3), as maiores estimativas de herdabilidade direta foram observadas ao nascimento (0,88) e aos 550 dias de idade (0,70), possivelmente devido ao menor número de animais com informações nessas idades, o que pode ter comprometido as estimativas dos componentes de variância. Entretanto, as estimativas para os pesos aos 120 (P120), 210 (P210), 365 (P365) e 450 (P450) dias de idade também foram expressivas, com tendência de aumento (0,38, 0,32, 0,47 e 0,53, respectivamente). Comportamento similar foi relatado por Sousa Júnior et al.⁽¹⁶⁾ para a raça Tabapuã, por Meyer⁽¹⁹⁾ para bovinos da raça Hereford e por Albuquerque e El Faro⁽²⁰⁾ para a raça Nelore. Esses autores reportaram redução nas estimativas de herdabilidade direta após o nascimento, aumentando com o avanço da idade do animal. Resultados médios obtidos para a herdabilidade direta descritos na literatura para P120, peso aos 240 dias (P240), peso ao ano (P365) e P550 (0,23; 0,21; 0,30 e 0,41, respectivamente) foram menores aos estimados no presente trabalho^(21-23). Os valores das herdabilidade direta sugerem que, na população estudada, existe variabilidade genética suficiente para se obter ganho genético considerável, por meio da seleção, principalmente a partir da desmama, visto que as estimativas praticamente se mantiveram constantes e altas.

A herdabilidade materna estimada pelo melhor modelo (PL432_8) aumentou do nascimento até os 45 dias de idade (0,10), diminuindo gradativamente até os 550 dias de idade. A influência do efeito materno na fase inicial de vida no animal foi expressiva até próximo aos 90 dias de idade, indicando que os maiores ganhos na seleção para habilidade materna podem ser esperados próximos a essa idade. As estimativas de herdabilidades maternas para peso ao nascimento (PN), P240, P365 e P550 foram de 0,03; 0,05; 0,04 e 0,02, respectivamente. Os valores médios de herdabilidade materna relatados por Ferraz Filho et al.⁽²³⁾, Siqueira et al.⁽²⁴⁾ e Marcondes et al.⁽²¹⁾ foram superiores para P240 (0,19) e P365 (0,18), porém semelhantes para o P550 (0,02).

A variância de ambiente permanente de animal como proporção da variância fenotípica diminuiu do nascimento, chegando à zero aos 15 dias de idade, seguido por um aumento até os 180 dias de idade (0,43), próximo à fase de desmama dos animais (Figura 2, à direita). Após os 180 dias de idade, os valores foram decrescendo até os 550 dias de idade (0,15). Comportamento semelhante foi relatado por Sousa Júnior et al.⁽¹⁶⁾, para a raça Tabapuã, utilizando modelos de regressão aleatória. As estimativas de correlações genéticas aditivas diretas (Tabela 3) entre o PN e pesos subsequentes foram positivas de alta magnitude, sendo maiores em idades mais jovens, sugerindo que a seleção de animais para maiores pesos em idades jovens ocasionará aumento do PN e, consequentemente, a probabilidade de ocorrência de partos distócicos. Valores de correlações genéticas maiores foram relatados por Boligon et al.⁽²²⁾ para a raça Nelore entre PN e P240 (0,80) e o P550 (0,74), enquanto Albuquerque e El Faro⁽²⁰⁾ encontraram valores menores entre PN e o peso aos 120 (0,77) e 205 dias de idade (0,45) também para a raça Nelore.

Esses valores de correlação genética sugerem que os genes responsáveis pela expressão do peso em determinada idade são os mesmos para as outras idades. Ou seja, a seleção para aumentar o peso pode ser realizada em qualquer idade. No entanto, deve-se preconizar que a seleção em idades jovens privilegia animais mais precoces e possivelmente a maximização dos lucros dos sistemas de criação de bovinos de corte. Com exceção das estimativas de correlações genéticas aditivas maternas de PN com P120 (-0,37) e P210 (-0,21), todas as demais foram positivas, com tendência de diminuição com o aumento da distância entre as idades. Portanto, exceto para PN, quanto mais próximas as idades, maior a correlação entre os efeitos maternos. Sousa Junior et al.⁽¹⁶⁾ e Albuquerque e El Faro⁽²⁰⁾ relataram comportamento similar para bovinos da raça Nelore, pois observaram diminuição nos valores das correlações genéticas entre o PN e pesos posteriores. A análise dos quatro primeiros autovalores da matriz de covariância do efeito genético aditivo direto explicaram 100% da variação genética aditiva total, sendo que cada um foi responsável por 79,28%; 12,67%; 7,02% e 1,04% dessa variação, respectivamente (Figura 3).

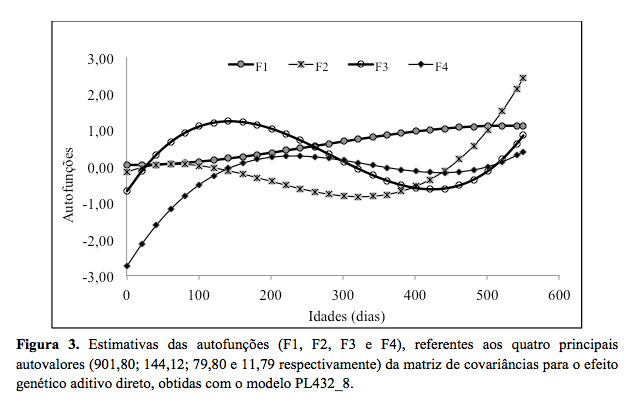
O primeiro autovalor explicou a maior parte da variação e sua autofunção (F1) foi positiva para todas as idades. No entanto, segundo Van der Werf⁽²⁵⁾, o sinal dos valores das autofunções não é importante para a interpretação dos resultados; o que se deve considerar, contudo, é a trajetória que as mesmas podem assumir durante o crescimento do animal, pois indicam a magnitude do autovalor associado a cada autofunção e as prováveis direções de seleção. Dessa forma, a seleção para a primeira autofunção pode resultar em mudanças no mesmo sentido para a característica peso em diferentes idades assim como observada nas correlações genéticas. Comportamento semelhante foi observado por Boligon et al.⁽²⁶⁾ em bovinos da raça Nelore, em que a seleção para a primeira autofunção pode resultar em mudanças no mesmo sentido para os pesos em diferentes idade. A segunda autofunção (F2) foi negativa até os 20 dias de idade, passando a ser positiva até os 100 dias de idade, tornando-se negativa até os 440 dias de idade e posteriormente foi positiva até os 550 dias de idade. A alteração no sinal sugere que a seleção sobre este componente promoverá efeitos contrários no início e no final da trajetória. Entretanto, considerando-se que o segundo autovalor explica uma menor fração da variação genética aditiva (12,67%), a possibilidade de mudança genética por seleção sobre esse componente pode ser menor. Esses resultados apresentam o mesmo comportamento que os descritos por Albuquerque e Meyer⁽¹⁵⁾ em bovinos da raça Nelore. A terceira e a quarta autofunção (F3 e F4) tiveram comportamento oscilatório de negativo a positivo, sendo de pouca importância, uma vez que juntas explicam pouca variância genética aditiva direta (8,06%) e, portanto, as possibilidades de alteração genética por seleção com base em suas autofunções pode ser limitada.

Conclusões

Modelos de regressão aleatória foram eficientes para estimar, com grande acurácia, (co)variâncias e parâmetros genéticos, em dados longitudinais de pesos de bovinos da raça Guzerá. Existe variabilidade genética aditiva suficiente para promover ganhos genéticos satisfatórios para o desempenho ponderal desde idades iniciais.

Agradecimentos

Os autores agradecem à Universidade Federal do Tocantins pelo apoio financeiro (Edital Propesq/UFT nº 21/2014) e à ANCP pela concessão dos dados.

Referências

1. Bertipaglia TS, Carreño LOD, Machado CHC, Andrighetto C, Fonseca Rd. Estimates of genetic parameters for visual scores and their correlation with production and reproductive traits in Brahman cattle. Revista Brasileira de Zootecnia. 2012;41(6):1407-11.
2. Boligon A, Mercadante M, Baldi F, Lôbo R, Albuquerque L. Multi-trait and random regression mature weight heritability and breeding value estimates in Nelore cattle. South African Journal of Animal Science. 2009;39(5):145-8.
3. Kirkpatrick M, Hill WG, Thompson R. Estimating the covariance structure of traits during growth and ageing, illustrated with lactation in dairy cattle. Genetical research. 1994;64(01):57-69.
4. Meyer BK. Estimates of genetic and phenotypic covariance functions for postweaning growth and mature weight of beef cows. Journal of Animal Breeding and Genetics. 1999;116(3):181-205.
5. ALBUQUERQUE LG. Regressão aleatória: nova tecnologia pode melhorar a qualidade das avaliações genéticas. 2004. In: Simpósio Brasileiro de Melhoramento Animal, 5, 2004. Pirassununga, SP. Anais… Pirassununga: SBMA, 2004. (CD-ROM). Disponível em: http://sbmaonline.org.br/anais/v/palestras/pdfs/palest11.pdf, Acesso em janeiro de 2017.
6. Van der Werf J, Schaeffer L. Random regression in animal breeding. Course notes CGIL Guelph. 1997.
7. Albuquerque LGd, Meyer K. Estimates of covariance functions for growth of Nelore cattle applying a parametric correlation structure to model within-animal correlations. Livestock Production Science. 2005;93(3):213-22.
8. Meyer K. Random regressions to model phenotypic variation in monthly weights of Australian beef cows. Livestock Production Science. 2000;65(1):19-38.
9. El Faro L, Albuquerque LGd. Utilização de modelos de regressão aleatória para produção de leite no dia do controle, com diferentes estruturas de variâncias residuais. Revista Brasileira de Zootecnia. 2003;32(5):1104-13.
10. Sakaguti E, Silva M, Martins E, Lopes P, Silva L, Quaas R, et al. Trajetória de crescimento e efeito da idade da vaca nos modelos de regressäo aleatória de bovinos jovens da raça Tabapuä. Arq bras med vet zootec. 2002;54(4):414-23.
11. Helwig JT, Council K. Statistical analysis system user's guide. Carey, NC, SAS Institute Inc. 1979:221-36.
12. Roso V, Schenkel F, editors. AMC-a computer programme to assess the degree of connectedness among contemporary groups. Proceedings of the 8th World Congress on Genetics Applied to Livestock Production, Belo Horizonte, Minas Gerais, Brazil, 13-18 August, 2006; 2006: Instituto Prociência.
13. Meyer K. WOMBAT—A tool for mixed model analyses in quantitative genetics by restricted maximum likelihood (REML). Journal of Zhejiang University Science B. 2007;8(11):815-21.
14. Huisman A, Veerkamp R, Van Arendonk J. Genetic parameters for various random regression models to describe the weight data of pigs. Journal of Animal Science. 2002;80(3):575-82.
15. Albuquerque LGd, Meyer K. Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle. Journal of animal science. 2001;79(11):2776-89.
16. Sousa Júnior SCd, Oliveira SMPd, Albuquerque LGd, Boligon AA, Martins Filho R. Estimação de funções de covariância para características de crescimento da raça Tabapuã utilizando modelos de regressão aleatória. Revista Brasileira de Zootecnia. 2010:1037-45.
17. Dias LT, Albuquerque LGd, Tonhati H, Teixeira RdA. Estimação de parâmetros genéticos para peso do nascimento aos 550 dias de idade para animais da raça Tabapuã utilizando-se modelos de regressão aleatória. Revista Brasileira de Zootecnia. 2006;35(5):1915-25.
18. Ferreira JL. Efeito da estrutura dos dados sobre as estimativas de (co) variâncias de peso à desmama em bovinos de corte, usando dados simulados: Universidade Federal de Goiás; 2009 (Tese de doutorado). Disponível em: https://repositorio.bc.ufg.br/tede/handle/tde/1177
19. Meyer K. Estimates of direct and maternal covariance functions for growth of Australian beef calves from birth to weaning. Genetics Selection Evolution. 2001;33(5):1.
20. de Albuquerque LG, ElFaro L. Comparações entre os valores genéticos para características de crescimento de bovinos da raça Nelore preditos com modelos de dimensão finita ou infinita. R Bras Zootec. 2008;37(2).
21. Marcondes C, Gavio D, Bittencourt T, Rocha J, Lôbo R, Bezerra L, et al. Estudo de modelo alternativo para estimaçäo de componentes de (co) variância e prediçäo de valores genéticos de características de crescimento em bovinos da raça Nelore. Arq bras med vet zootec. 2002;54(1):93-9.
22. Boligon AA, ALBUQUERQUE Ld, Rorato PRN. Associações genéticas entre pesos e características reprodutivas em rebanhos da raça Nelore. Revista Brasileira de Zootecnia. 2008;37(4):596-601.
23. Ferraz Filho PB, de Amorim Ramos A, da Silva LOC, de Souza JC, de Alencar MM, Malhado CHM. Tendência genética dos efeitos direto e materno sobre os pesos à desmama e pós-desmama de bovinos da raça Tabapuã no Brasil. R Bras Zootec. 2002;31(2):635-40.
24. de Siqueira RLPG, de Oliveira JA, Lôbo RB, Bezerra LAF, Tonhati H. Análise da variabilidade genética aditiva de características de crescimento na raça Nelore. R Bras Zootec. 2003;32(1):99-105.
25. Van der Werf J. 2001. Random regression in Animal Breeding: course notes. Disponível em: http: www-personal.une.edu.au=~jvanderw/CFcoursenotes.pdf. Acesso em: 20 dez. 2013.
26. Boligon AA, Mercadante MEZ, Forni S, Lôbo RB, Albuquerque LGd. Covariance functions for weights from birth to maturity in Nellore cows. Journal of Animal Science, 2010; 88:849-859./http: