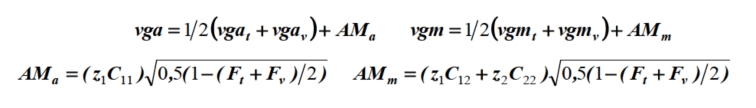
EFEITOS DA
INCLUSÃO OU NÃO DA COVARIÂNCIA GENÉTICA DIRETA-MATERNAL NO MODELO E DOS VALORES
REAIS DAS (CO)VARIÂNCIAS SOBRE SUAS ESTIMATIVAS PARA PESO À DESMAMA EM BOVINOS
DE CORTE
Jorge Luis
Ferreira1, Arcadio de los Reyes Borjas2, Roberto
Carvalheiro3, Raysildo Barbosa Lôbo4
1 – Professor Doutor
Universidade Federal do Tocantins. Araguaína, TO
2 - Professor Titular do
Departamento de Produção Animal, da Escola de Veterinária e Zootecnia da
Universidade Federal de Goiás. Goiânia, GO.
3 - Pós-doutor Gensys
Cosultoria. Porto Alegre, RS
4 -
Professor Associado da FMRP-USP. Diretor-Presidente da ANCP, Ribeirão Preto, SP
RESUMO
Objetivou-se
estimar e comparar componentes de (co)variâncias para peso a desmama em
bovinos, considerando-se os efeitos da correlação genética direta-maternal
(-0,50; -0,25; +0,25; +0,50), da razão entre as variâncias genéticas direta e
maternal (75:75; 50:100; 100:50), e da inclusão (M2) ou não (M1) no modelo da
covariância genética direta-maternal. Foi realizada simulação estocástica de 20
réplicas de um rebanho fechado, em acasalamento aleatório, durante 20 anos de
seleção, com animais base não aparentados, não selecionados e amostrados
aleatoriamente. As estimativas de (co)variâncias foram obtidas sob modelo
animal unicarácter, usando o aplicativo MTDFREML. Os cenários simulados foram
constituídos pelas combinações dos níveis dos três efeitos estudados. O modelo
influenciou significativamente (p<0,05) as estimativas de variâncias
genéticas direta, maternal e residual, não sendo significativo sobre a
variância de ambiente permanente maternal. O valor da correlação genética
direta-maternal influenciou significativamente (p<0,05) todas as
(co)variâncias, e a razão de variâncias exerceu efeito significativo
(p<0,05) apenas sobre as estimativas de variâncias genéticas direta e
maternal. Quando a correlação genética direta-maternal foi negativa o M1
subestimou as variâncias direta e maternal, e quando positiva superestimou as
mesmas. Estimativas confiáveis e acuradas das (co)variâncias para peso a
desmama em bovinos de corte são dependentes da adequação do modelo, bem como
dos valores reais das (co)variâncias sendo estimadas.
---------------------
EFFECTS OF NON-INCLUSION OF GENETIC
DIRECT-MATERNAL COVARIANCE IN THE MODEL AND REAL VALUES OF (CO)VARIANCES ON
THEIR ESTIMATES FOR WEANING WEIGHT IN BEEF CATTLE.
ABSTRACT
Quando os efeitos maternais são
ignorados há superestimativa da herdabilidade direta (KOCH, 1972), o que pode
conduzir a conclusões errôneas, porque toda a variância encontrada, excetuando-se
a residual, terá origem atribuída ao efeito genético direto.
MEYER (1992) estimou
(co)variâncias para pesos à desmama, em bovinos Hereford, Angus e Zebu cruzado
na Austrália, através de seis diferentes modelos, verificando que, quando os
efeitos maternais foram ignorados, a herdabilidade direta foi inflada
substancialmente.
DIOP et al. (1999) testaram a
inclusão dos efeitos de avós no modelo animal com efeitos maternos em animais
da raça Gobra, no Senegal, e sugeriram que o valor negativo da correlação
genética entre os efeitos direto e materno podia estar relacionado com as
condições ambientais em que os animais foram manejados.
Assim, diante das incertezas,
tem sido proposto considerar como igual a zero (SCHAEFFER, 2010) a correlação
genética entre os efeitos direto e maternal. No entanto, os modelos que a
consideram, revelaram serem os mais indicados.
Dessa forma, objetivou-se
estimar componentes de (co)variâncias para peso à desmama em bovinos de corte,
comparando-se modelos que incluíram ou não a covariância genética direta
maternal, sobre dados simulados.
Nos anos seguintes, o critério
de seleção de machos e fêmeas também se baseou no valor genético individual. A
reposição foi efetuada com animais nascidos três anos antes no próprio rebanho,
produzindo sete gerações sobrepostas ao longo dos 20 anos. Dessa forma, houve
nascimento anual de 724 bezerros, distribuídos aleatoriamente em 40 grupos
contemporâneos (GC), 20 constituídos por machos e os demais por fêmeas. Para
garantir a conexidade genética entre os GC foram impostas restrições sobre os
números mínimos de filhos por touro (5), bezerros por GC (5), touros por GC
(2), conforme proposto por SCHAEFFER (2010).
Como característica sob efeito maternal, considerou-se o peso à desmama (PD), cujo valor para os machos foi acrescido em 15 kg, em relação às fêmeas. Neste caso, a simulação dos efeitos genéticos direto e maternal foi gerada simultaneamente, já que tais efeitos são geneticamente correlacionados (SCHAEFFER, 2010). Esse processo sustenta-se na decomposição de Cholesky da matriz G de (co)variâncias genéticas, a qual pode ser expressa pelo produto de uma matriz vezes sua transposta, isto é:
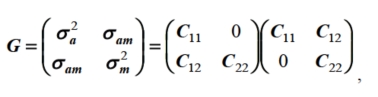
em que C
é uma matriz triangular inferior com os valores C11, C12
e C22 correspondentes às
componentes σ²a, σ²am
e σ²m,
respectivamente.
Os valores egc,
ap e e foram amostrados de distribuição Normal com média zero e
variâncias σ²egc
(egc~N(0, 450)), σ²ap
(ap~N(0, 45)) e σ²e (e~N(0,
225)), respectivamente. Nas gerações seguintes à população base, os valores
genéticos aditivos direto (vga) e
maternal (vgm) de cada indivíduo
foram calculados conforme as equações a seguir:
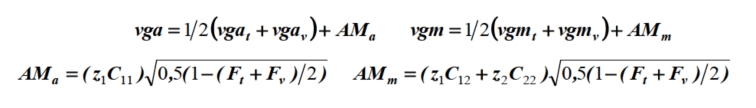
em que: vga
= valor genético aditivo direto do bezerro; vgm
= valor genético aditivo maternal do bezerro; vgat = valor genético aditivo direto do touro; vgav = valor genético aditivo
direto da vaca; vgmt =
valor genético aditivo maternal do touro; vgmv
= valor genético aditivo maternal da vaca; AMa,
AMm = contributos da
amostragem Mendeliana aleatória aos valores genéticos aditivos direto e
maternal, respectivamente; z1,
z2 = desvios normais
aleatórios; C11, C12, C22 = termos da decomposição de Cholesky da matriz G, correspondentes às componentes σ²a, σ²am
e σ²m,
respectivamente; Ft e Fv = coeficientes de
consanguinidade do touro (pai) e da vaca (mãe), respectivamente. A partir do
quarto ano aconteceram acasalamentos entre parentes, gerando indivíduos com
algum grau de consanguinidade, parte dos quais acasalaram a partir do sétimo
ano. Os efeitos da amostragem Mendeliana assumiram-se independentes de vgat, vgav, vgmt
e vgmv (BULMER, 1971). A
decomposição de Cholesky da matriz de (co)variâncias genética (G) foi obtida por meio da função root do PROC IML do SAS (2002).
As estimativas de (co)variâncias e as predições de
valores genéticos, foram obtidas pelo método de Máxima Verossimilhança Restrita
(REML) através de modelo animal unicaráter, usando o aplicativo MTDFREML (Multiple-Trait Derivative-Free Restricted
Maximum Likelihood), desenvolvido por BOLDMAN et al. (1995).
O modelo linear misto para descrever cada
observação foi:
Y = Xß + Z1a + Z2m + Z3ap
+ e
em que; Y = vetor das observações da
característica (PD); X = matriz de incidência dos efeitos
fixos; ß = vetor dos efeitos
fixos; Z1 = matriz de incidência do efeito genético aditivo
direto de cada animal; a = vetor de efeitos aleatórios
genéticos aditivos diretos; Z2 = matriz de incidência
do efeito genético aditivo maternal de cada animal; m = vetor de efeitos
aleatórios genéticos aditivos maternais; Z3 = matriz de incidência
do efeito do ambiente permanente maternal; ap = vetor de efeitos aleatórios do
ambiente permanente maternal; e = vetor de efeitos aleatórios
residuais.
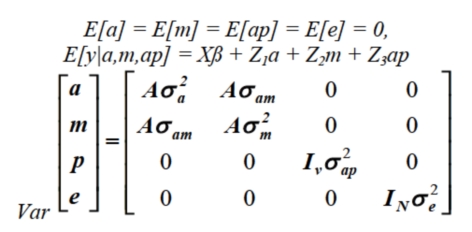
em que: σ²a ![]() = variância genética aditiva direta; σ²m
= variância genética aditiva maternal; σam
= covariância genética entre os efeitos aditivos direto e maternal; A = matriz de parentesco; σ²ap
= variância do ambiente permanente maternal; σ²e =
variância residual; Iv, IN = matrizes identidade de ordens; v = número
de vacas (mães dos animais com dados) e N = número total de animais com dados.
= variância genética aditiva direta; σ²m
= variância genética aditiva maternal; σam
= covariância genética entre os efeitos aditivos direto e maternal; A = matriz de parentesco; σ²ap
= variância do ambiente permanente maternal; σ²e =
variância residual; Iv, IN = matrizes identidade de ordens; v = número
de vacas (mães dos animais com dados) e N = número total de animais com dados.
Dois modelos de análises foram usados para estimar
os componentes de (co)variâncias: M1 - modelo animal que considerou
a covariância genética entre os efeitos direto e maternal igual a zero (cov=0);
e M2 em que o valor da covariância genética direta-maternal foi
considerado conforme a simulação dos dados.
O modelo linear misto para descrever cada
observação, foi:
Y = Xß + Z1a + Z2m + Z3ap
+ e
em que: Y = vetor das observações da
característica (PD); X = matriz de incidência dos efeitos
fixos; ß = vetor dos efeitos
fixos; Z1 = matriz de incidência do efeito genético aditivo
direto de cada animal; a = vetor de efeitos aleatórios
genéticos aditivos diretos; Z2 = matriz de incidência
do efeito genético aditivo maternal de cada animal; m = vetor de efeitos
aleatórios genéticos aditivos maternais; Z3 = matriz de incidência
do efeito do ambiente permanente maternal; ap = vetor de efeitos aleatórios do
ambiente permanente maternal; e = vetor de efeitos aleatórios
residuais.
Os cenários foram constituídos considerando-se
quatro valores de correlação genética (-0,50; -0,25; +0,25 e +0,50), três
razões entre as variâncias genéticas direta e maternal (75:75; 50:100; 100:50)
e dois modelos (M1 e M2). Dessa forma, foram constituídos
24 cenários (4 (C) x 3 (R) x 2 (M)) = 24 cenários).
As estimativas de (co)variâncias obtidas em cada
cenário, foram submetidas à analise de variância pelo procedimento GLM (General Linear Model) pelo sistema de
analises estatísticas (SAS, 2002), conforme o modelo:
Yijkl = µ
+ Ci + Rj + Mk + (Interações Duplas) +
(Interação Tripla) + eijkl
em que: Yijkl=
estimativas de (co)variâncias (i.e., σ²a,
σ²m, σ²p, σ²e); µ= média
geral; Ci= efeito do i-ésimo valor da correlação genética
direta-maternal (-0,50; -0,25; +0,25 e +0,50); Rj= efeito da j-ésima razão entre
variâncias genéticas direta e maternal (75:75; 50:100; 100:50); Mk=
efeito do k-ésimo modelo (M1 e M2); Interações Duplas = Ci
x Rj; Ci x Mk;
Rj x Mk; Interação
Tripla = Ci x Rj x Mk; eijkl =
efeito residual aleatório.
O erro padrão quadrático (EP)2 da média das 20 réplicas para
cada cenário foi usado como fator de ponderação nas análises. A significância
de cada efeito sobre as estimativas de (co)variâncias foi testada pelo
procedimento GLM do SAS (2002). O erro padrão (EP) das estimativas de cada
cenário foi utilizado como critério de precisão e o viés médio, como critério
de acurácia.
A interação CxR não foi significativa para as
estimativas de variância genética maternal, enquanto que as estimativas da
variância de ambiente permanente maternal não foram significativamente
influenciadas pela interação CxM. A
interação CxR teve contribuição
importante ao ajuste do modelo, para as estimativas da variância de ambiente
permanente maternal (8%), sendo reduzida (0,7% e 1%) para as demais estimativas
(i.e., σ²a, σ²e).
A interação CxM teve efeito significativo (p<0,0001) sobre as estimativas da variância genética maternal, variância genética direta e variância residual, contribuindo ao ajuste do modelo com 9%, 11% e 26%, respectivamente.
O efeito do modelo não foi significativo sobre as estimativas de variância genética maternal e variância de ambiente permanente maternal. Os resultados no modelo que não considerou a covariância genética direta-maternal (M1), para as estimativas de variâncias genéticas direta e maternal, mostraram um viés negativo de (-31,36% e -15,62%; -36,61 e -13,23) respectivamente, quando a correlação genética direta-maternal foi negativa (-0,50 e -0,25).
Entretanto, quando a correlação
genética direta-maternal foi positiva (+0,25 e +0,50), no mesmo modelo, houve
aumento na magnitude das estimativas de variâncias genéticas dos efeitos direto
e maternal, sendo as mesmas superestimadas.
No modelo que incluiu a
covariância genética direta-maternal (M2), obteve-se o menor viés
das estimativas de variâncias genéticas direta e maternal, com magnitudes de
(3,3 e 1,0) e (1,38 e 3,69) kg2, quando C= -0,50 e -0,25,
respectivamente, e (0,99 e 4,35) e (0,71 e 3,57) kg2, quando C=
+0,25 e +0,50, respectivamente.
Estes resultados concordam com
os reportados por HEYDARPOUR et al. (2008) em estudo de simulação. E de forma similar, aos reportados
por CLÉMENT et al. (2001) que observaram que a confiabilidade das estimativas
de (co)variâncias foi dependente do valor da correlação genética real nos
dados.
Quando a correlação genética
direta-maternal é considerada igual a zero (M1), os valores das
estimativas de variância genética direta e maternal são sempre viesados.
Assim, verificou-se que quando a
correlação genética direta-maternal foi negativa (-0,50 e -0,25) as estimativas
de variância genética direta e maternal foram subestimadas, chegando a 1,32
vezes menor que o valor real. E quando a correlação genética direta-maternal
foi positiva (+0,25 e +0,50) as estimativas de variâncias genética direta e
maternal foram superestimadas, chegando a 0,77 vezes maior que o valor real.
Corroborando os resultados encontrados por CLÉMENT et al. (2001) que
demonstraram que quando a correlação genética direta-maternal é considerada
nula, os valores das estimativas de variância genética direta e da
herdabilidade direta são superestimados, chegando às vezes, esse valor, a
duplicar em relação aos valores verdadeiros.
As interações RxM e CxRxM não exerceram efeitos significativos sobre as estimativas de
(co)variâncias para peso a desmama em bovinos de corte.
Dessa forma, assumindo que as
condições aqui simuladas sejam similares às dos dados reais, revela-se que a
utilização de modelos que não incluem a covariância genética direta-maternal
determinam estimativas não confiáveis, comprometendo as estimações das
(co)variâncias, dos parâmetros genéticos e da ordem de classificação dos
animais pelos seus valores genéticos preditos.
Observou-se no M2 que,
o viés médio nos diferentes cenários, das estimativas de variâncias genéticas
direta e maternal e variância residual foram de +2,21; +2,19 e -0,02,
respectivamente. Sob o modelo (M2), as estimativas mais acuradas e
precisas, para as variâncias genéticas direta e maternal e a variância
residual, foram obtidas quando C=+0,25 e a razão 1:1 entre variâncias genéticas
direta e maternal.
Na Figura 1 são apresentadas as
magnitudes do viés das estimativas de variâncias (%) e da covariância
direta-maternal (valor real), segundo valores reais da razão entre as
variâncias genéticas direta e maternal e da correlação genética
direta-maternal, sob modelos incluindo (M2) ou não (M1) a
covariância genética direta-maternal.
Na Figura 1 observa-se que sob o modelo M1, quando a correlação genética direta-maternal (C) foi negativa, as variâncias genéticas direta e maternal foram subestimadas, enquanto a variância residual foi viesada positivamente. Opostamente, quando C foi positiva, as σ²a e σ²m foram viesadas positivamente, com subestimação da σ²e.
Resultados similares foram reportados por CLÉMENT et al. (2001) que observaram que a confiabilidade das estimativas de (co)variâncias foram dependentes do valor real da correlação genética direta-maternal nos dados.
Diversos
autores (ELER et al., 1989; MEYER, 1992; FERNANDES & FERREIRA, 2000;
UTRERA, 2008) têm estimado
correlações genéticas de valor negativo entre os efeitos direto e maternal, com
dados de campo. Este antagonismo genético tem sido levado em conta nas
avaliações genéticas de muitas raças de bovinos de corte, com valores, em
média, -0,29
para Brangus, -0,21 para Gelbvieh, -0,29 para Beefmaster, -0,18
para Senepol e -0,09 para o Shortorn (BIF,
2010). Este mesmo guia recomenda também nas avaliações genéticas de algumas
raças, valor zero para a correlação genética entre os efeitos direto e
maternal, como Angus, Braford, Hereford, Limousin, Red Angus, Romagnola e Santa
Gertrudis.
Na realidade,
essas recomendações se baseiam principalmente na dificuldade da separação dos
diferentes efeitos e suas correlações sobre o desempenho fenotípico, presente
em dados de campo. SCHAEFFER (1984) discutiu os efeitos de valores de
correlação incorretos em análises multivariadas, concluindo que o PEV aumentou
com o uso incorreto de covariâncias. Da mesma forma, HENDERSON (1975) comentou que o uso de variâncias e matriz de
covariâncias incorretas no modelo misto faz aumentar as
variâncias dos erros de predição (PEV).
Nos gráficos
da Figura 1, observa-se que ao se considerar a covariância genética
direta-maternal igual a zero, em todos os cenários analisados, as estimativas
de (co)variâncias são todas viesadas. No entanto, quando a covariância foi
considerada diferente de zero, os vieses foram menores, e estimativas de
variâncias genéticas direta e maternal mais confiáveis foram obtidas quando a
variância direta foi maior que a maternal.
Assim, a
confiabilidade e precisão das estimativas de (co)variâncias e consequentemente
dos parâmetros genéticos é conseguida com modelos que incluem a covariância
genética direta-maternal.
As estimativas da variância
de ambiente permanente maternal foram todas viesadas negativamente, e deforma
similar em magnitude sob ambos os modelos (M1 e M2) e
para qualquer um dos cenários. Essa situação é extremamente particular e
curiosa, uma vez que no foi encontrado na literatura consultada nenhum
resultado referido ao viés da estimativa dessa variância.
A confiabilidade das
estimativas de variância residual foi maior no modelo que incluiu a covariância
genética direta-maternal (M2), indicando, mais uma vez, que a inclusão da
covariância genética direta-maternal no modelo é de extrema importância.
A maioria dos
resultados da literatura, para as estimativas das (co)variâncias de que trata o
presente trabalho, mostram correlação negativa, de média a alta entre os
efeitos genéticos aditivos direto e maternal, e estimativas superiores da
variância genética direta relativo à maternal. Como exemplo, UTRERA (2008)
encontraram para peso a desmama, estimativas médias de herdabilidade direta,
maternal e correlação genética entre os efeitos direto e maternal, da ordem de
0,27, 0,17 e -0,23, respectivamente.
Assim,
assumindo as condições simuladas semelhantes daquelas dos dados reais, fica
claro que o modelo que inclui a covariância genética direta-maternal permite as
estimativas mais confiáveis das (co)variâncias, exceto a variância de ambiente
permanente maternal, o qual se ilustra no lado esquerdo dos gráficos da Figura
1 (correlações reais 1 e 2) para a razão de variâncias direta/maternal 2:1.
A recomendação de vários
autores de não considerar a covariância genética direta-maternal no modelo de
análise não parece uma boa estratégia para estimação de (co)variâncias e
parâmetros genéticos do crescimento até a desmama, pois verificou-se que isto
leva a estimativas viesadas das (co)variâncias, interferindo nas estimativas
dos parâmetros genéticos, na predição dos valores genéticos dos animais e no
ganho genético por seleção.
BIF. Guidelines for uniform beef improvement programs (9th
Ed.), Beef Improvement Federation, USA. 2010. Disponível em: http://www.beefimprovement.org/PDFs/guidelines/2010%20Guidelines%20,%209th%20Edition.pdf. Acesso em 03/06/2011.
BOLDMAN, K.G., KRIESE, L.A., VAN VLECK, L.D.,
VAN TASSELL, C.P., KACHMAN, S.D. A manual for use of MTDFREML: a set of programs to obtain estimates of
variances and covariances [DRAFT].
Lincoln: Department of Agriculture/Agriculture Research Service, 1995.115p.
BULMER, M.G., The effect of selection
on genetic variability. The American Naturalist,
v.105, p.201-211, 1971.
CLÉMENT, V., BIBÉ, B., VERRIER, E., ELSEN, J.M.,
MANFREDI, E., BOUX, J., HANOCQ, E. Simulation analysis to test the influence of
model adequacy and data structure of genetic parameters for traits with direct
and maternal effects. Genetics Selection Evolution, v.33, 369-395, 2001.
DIOP, M., DODENHOFF, J., Van
VLECK, L. D. Estimates of direct, maternal and grandmaternal genetic effects
for growth traits in Gobra cattle. Genetics
and Molecular Biology, v. 22, n. 3, p.
363-367,1999.
ELER, J.P., LÔBO,
R.B., DUARTE, F.A.M. Avaliação dos efeitos genéticos direto e materno em pesos
de bovinos da raça Nelore criados no Estado de São Paulo. Revista Brasileira de Zootecnia, v.18, n.2, p.112-123, 1989.
FERNANDES, H.D.,
FERREIRA, G.B. Estudo comparativo de sete diferentes modelos estatísticos para
a característica ganho de peso em bovinos de corte. Revista
Brasileira de Zootecnia, v.29, n.5, p.1340-1348, 2000.
GERSTMAYR, S. Impact of the
data structure on the reliability of the estimated genetic parameters in an
animal model with maternal effects, Journal of Animal
Breeding Genetics v.109, p.321-326, 1992.
HENDERSON, C.R. Comparison of
alternative sire evaluation methods. Journal of Animal Science, v.41, p.760-770,
1975.
HEYDARPOUR, M., SCHAEFFER, L., YAZDI, H.
Influence of population structure on estimates of direct and maternal
parameters. Journal of Animal Breeding
Genetics, v.125, p.89-99, 2008.
KOCH, R.M. The role of maternal
effects in animal breeding: VI. Maternal effects in beef cattle. Journal of Animal Science, v.35,
p.1316-1323, 1972.
MANIATIS, N., POLLOT, G.E. The impact of data
structure on genetic (co)variance components of early growth in sheep,
estimated using an animal model with maternal effects. Journal of Animal Science, v.81, p.101-108,
2003.
MEYER, K. Bias and sampling covariances of estimates
of variance components due to maternal effects. Genetics Selection Evolution., v. 24, p.487-509,
1992.
ROEHE, R., KENNEDY, B.W. The
influence of maternal effects on accuracy of evaluation of litter size in
swine. Journal of
Animal Science, v.71, p.2353-2364, 1993.
SCHAEFFER, L. R. Sire and cow
evaluation under multiple trait models. Journal
of Dairy Science, v. 67, p.1567-1580, 1984.
SCHAEFFER, L.R. Linear Models
and Animal Breeding. Centre for
Genetic Improvement of Livestock. Department of Animal and Poultry Science, 2010. European course. 314 p. Disponível em: http://www.aps.uoguelph.ca/~lrs/ABModels/DATA/EuropeNotes.pdf. Acesso em 20/07/2011.
STATISTICAL ANALYSIS SYSTEMS – SAS. User’s guide. Version 8.2. 1 ed. Cary: 956p. 2002.
UTRERA,
A. Estimadores de parámetros genéticos para características de crecimiento
predestete de bovinos. Revisión. Técnica
Pecuaria en México, v. 46, p. 37-67, 2008.
ZAMANI, P., MOHAMMADI, H. Comparison of different models for estimation of genetic parameters of early growth traits in the Mehraban sheep. Journal of Animal Breeding and Genetics, v.125, n.1, p.29-34, 2008.