Introduction

Pangolão grass (Digitaria pentzii Stent.) is a grass originating in Zimbabwe and the surrounding area in Africa. It is a species adapted to a wide diversity of soils and requires annual average rainfall greater than 380 mm and air temperature between 14 and 34 °C for its establishment and development⁽¹⁾.

The leaf is the morphological structure of light interception for photosynthesis, responsible for gas exchange and carbohydrate, lipid, and protein production⁽²⁾. Thus, leaf area determination (as leaf area ratio, specific leaf area, and leaf area index) is a tool used to evaluate various processes that occur in the plant^(3-4).

Leaf area can be estimated directly and indirectly, destructively and non-destructively. In direct destructive estimation, a high degree of manpower is used, and all plant leaves are collected. The direct and non-destructive method is dependent on equipment and is typically expensive⁽⁵⁾. Indirect and non-destructive methods that can be used to rapidly and repeatedly evaluate the same plant are becoming more convenient; these methods are less harmful as there is preservation of the leaves^(3-6-7).

Statistical modeling using linear dimensions as explanatory variables to estimate the real leaf area has become a very useful and inexpensive method to study plant growth and development, eliminating the need for expensive equipment or lengthy geometric reconstruction⁽⁸⁾. Several studies have been performed for different cultures: Urochloa mosambicensis⁽⁹⁾, Brachiaria brizantha, and Panicum maximum⁽¹⁰⁾, passion fruit⁽¹¹⁾, vine⁽³⁾, mango⁽¹²⁾, and pineapple⁽¹³⁾ and have generated models with high precision.

The agronomic characteristics of pangolão grass have been studied; however there are few studies on leaf blade area estimation for this species. The objective of this study was to estimate the leaf blade area of pangolão grass, using non-destructive methods through regression model analysis.

Materials and methods

The research was conducted from February to July 2018 by the Study Forragiculture Group (GEFOR) in Unidade Acadêmica de Serra Talhada, Universidade Federal Rural de Pernambuco, located in the municipality of Serra Talhada, (latitude: 7º 56' 15" S and longitude: 38º 18' 45" W) at an altitude of 429 m. According to the Köppen classification, the climate is type BSwh', with an average annual rainfall of 632 mm year-¹ and air temperatures higher than 25 ºC⁽⁹⁾.

The soil utilized in this study was Eutrophic Ta Haplic Cambisol⁽¹⁴⁾, collected at a depth of 0-20 cm from the profile (posteriorly), homogenized, and penetrated. About 10.0 kg soil was placed in plastic pots with volume of 14.42 dm³, drilled at the bottom, and with a 2.0 cm layer of gravel for drainage of irrigation water.

The chemical attributes of the soil were characterized by Empresa Pernambucana de Pesquisa Agropecuária (IPA): pH (water) = 7.20; P (Mehlich I extractor) = 40 mg dm^-3; K+ = 0.45; Ca²⁺ = 5.3; Mg²⁺ = 1.1; Na+ = 0.06; Al³⁺ = 0.0; H⁺ = 1.23; SB = 6.91; CTC = 8.14 (cmolc dm^-3); and V = 84.89%.

Two tillers of pangolão grass (Digitaria pentzii Stent.) were planted per pot. All plants were maintained at field capacity using the gravimetric method for the first 30 days after planting (DAP). Water content of the experimental unit was monitored daily according to recommendation of Casaroli and Van Lier⁽¹⁵⁾.

At 31 DAP, when the seedlings were fully set, all the plants were submitted to a uniform cut, according to treatments (cutting heights of 10, 15, and 20 cm). The cuts were performed using pruning shears and a millimeter ruler.

All pots received N foundation fertilizer (50 kg N/ha, urea form) and P (50 kg P₂O₅/ha, simple superphosphate form), corresponding to 0.77 and 1.94 g/pot, respectively.

Throughout the experimental period, the plants were kept under field capacity, with irrigation every two days, and the pots were kept free of invasive plants.

The experimental design consisted of randomized blocks with three cutting heights (10, 15, and 20 cm) and four repetitions. At the end of three consecutive growth cycles of pangolão grass, the plants were cut (10, 15, and 20 cm) at 35-day intervals between cuts and separated into dead material (necrotic part of the senescent leaf), stem (including leaf sheaths), and leaf blades.

Randomly, 300 green leaf blades were collected, including expanded and unexpanded leaves, 100 for each treatment (cutting heights of 10, 15, and 20 cm). The collected leaf blades were completely intact and in different phenological stages of growth, as determined according to the methodologies of Leite et al.⁽⁹⁾ and Schmildt et al.⁽³⁾. All leaf blades were numbered and measured. Using a digital caliper, the length (L) and width (W) of each leaf were measured. Length was measured along the central rib and the width was determined at the median part of the leaf blade. The product of L and W (LW) was also determined.

All 300 pangolão grass leaf blades were drawn using graphite and graph paper. Posteriorly, the drawings were cut and weighed on an analytical balance. A square of graph paper of known size (10 cm x 10 cm) was drawn and cut; the estimated mass was 0.630 g. The real leaf area of each pangolão grass leaf blade was calculated proportionally to the square mass according to the methodology adapted from Leite et al.⁽⁹⁾.

The estimated leaf blade area of pangolão grass was determined with the use of regression models, using as response variable (Y_i) real leaf area (RLA) and as an explanatory variable the product of the length (L) and width (W) of each leaf blade, shown in the equations as LW_i. In the regression model analysis, we used the linear model with normal distribution and the power model, assuming the response of the response variable is in the range (-∞;∞).

Where Y_i is the ith leaf area; LW_i is the product of the length and width of the ith leaf blade; and ε_i is the ith error associated with leaf area, and εi represents normal distribution of mean 0 and constant variance σ² > 0 for linear and power models. β₀ and β₁ are the parameters to be estimated by the models.

Eight modelling scenarios were evaluated to estimate the leaf blade area of pangolão grass: two models (linear and power) for all four groups (three cutting heights and regardless of cutting height). Four criteria were adopted to evaluate the performance of the models: Akaike Information Criterion (AIC), sum of square of residuals (SSR), Willmott Index (d) and coefficient of determination of the model (R²).

AIC), according to Akaike⁽¹⁶⁾, is described by:

AIC =-2ln L(x\θ)+ 2(p)

where, L(x\θ) is the maximum likelihood function and p is the number of model parameters.

The sum of square of residuals (SSR) is the sum of the square of the difference between the observed values and the values predicted by the models, where the smallest value contributes to choosing the best equation. Let Ŷ₁ be the value of the ith leaf area after model adjustment; thus SSR is defined for this study by the following expression:

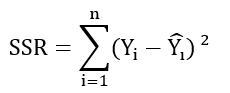
Index d, defined by Willmott⁽¹⁷⁾ is given by:

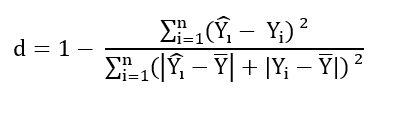
where, Y is the mean of the leaf area values (Y_i).

The coefficient of determination of the model (R²) is described by:

 

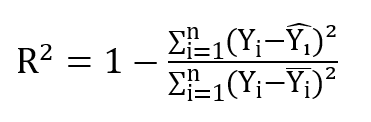
Results and discussion

As shown in Table 2, there was considerable variability in linear dimensions [length (L), width (W), LW, and real leaf area (RLA)]. This variability can be attributed to the fact that leaf blades (both young and mature) were randomly collected, thus allowing the determination of a single leaf blade area equation, can be used at any plant phenological stage. According to Cargnelutti Filho et al.⁽¹⁸⁾, a wide variability provided by maintaining extreme values is important in modeling, as it contributes to the representativeness of models. According to Schmildt et al.⁽³⁾, high-amplitude values are important in the representation of leaf area through regression model analysis.

Table 3 shows the regression models and the adequacy criteria of the models, using as an explanatory variable the product of the length and width of the leaf blade pangolão grass (LW). Both regression models (power and linear) reliably determined leaf area of pangolão grass at a cutting height of 10 cm.

The explanatory power of the linear model, when applied to plant samples at a cutting height of 15 cm, presented the lowest value. The power model presented the best adequacy criteria to estimate the leaf blade area of pangolão grass at cutting heights of 15 cm, 20 cm, and regardless of the cutting height (Table 3).

The determination coefficients (R²) of all models were higher than 0.96 (Table 3), indicating that the leaf area of D. pentzii can be explained by these models, resulting in high reliability estimates for this culture.

Silva et al.⁽¹⁰⁾, estimating leaf area of U. brizantha 'Xaraés' and Panicum maximum 'Massai', used LW as an explanatory variable and found linear equations with high coefficients of determination, concluding that such measures are adequate to estimate leaf area of tropical forage grasses.

Cardozo et al.⁽¹⁹⁾ found that the leaf area of Crotalaria juncea can be explained with high accuracy (R² > 97%) based on linear measurements. Queiroz et al.⁽²⁰⁾ estimated the leaf area of forest species using the LW product as an explanatory variable generating a higher coefficient of determination. Leite et al.⁽⁹⁾ verified that the power model presented the best estimates of leaf area of Urochloa mosambicensis using LW as the explanatory variable.

Conclusion

The results of our study indicate that the power model (Ŷ=LW^1.007) can be used to determine leaf area of pangolão grass (Digitaria pentzii Stent) regardless of the cutting height used to obtain samples. In the case of this species, the explanatory variable in the power model is the product of the length value (L) and width (W) of the leaf blade.

References