DOI: 10.1590/1089-6891v20e-49928
ZOOTECNIA

UTILIZAÇÃO DE MODELOS DE REGRESSÃO ALEATÓRIA PARA OBTENÇÃO DE PARÂMETROS GENÉTICOS DE BOVINOS DA RAÇA TABAPUÃ

USE OF RANDOM REGRESSION MODELS FOR ESTIMATION OF GENETIC PARAMETERS IN TABAPUÃ CATTLE

Severino Cavalcante Sousa Júnior^1* ORCID – http://orcid.org/0000-0002-8806-1179
Rogério Paes Sousa¹ ORCID – http://orcid.org/0000-0003-1259-5796
Karina Rodrigues Santos¹ ORCID – http://orcid.org/0000-0003-2872-0002
Luanna Chácara Pires² ORCID – http://orcid.org/0000-0002-7818-5899

¹Universidade Federal do Piauí, Teresina, PI, Brasil.
²Universidade Federal do Sul da Bahia, Teixeira de Freitas, BA, Brasil.
^*Autor para correspondência - sevzoo@yahoo.com.br

Resumo
Este trabalho utilizou 28.643 registros de pesos, do nascimento aos 660 dias de idade, de 6.471 animais da raça Tabapuã para estimar componentes de variância, covariância e parâmetros genéticos, utilizando o modelo de regressão aleatória. Foi utilizado algoritmo de busca AIREML através do método da máxima verossimilhança restrita pelo programa computacional DFREML. Os modelos incluíram: como aleatórios, os efeitos genético aditivo direto, materno, de ambiente permanente de animal e materno; como fixos, os efeitos de grupo de contemporâneos; como covariáveis, a idade do animal à pesagem e a idade da vaca ao parto. As estimativas de variância genética aditiva direta obtidas aumentaram com a idade. As estimativas de herdabilidade para o efeito aditivo direto mostram o decréscimo da herdabilidade do nascimento até a desmama, enquanto as estimativas de herdabilidade materna apresentaram aumento do nascimento até a desmama, decrescendo nas idades seguintes. As correlações genéticas diretas variaram de moderadas a altas, diminuindo suas magnitudes à medida que aumentou a distância entre as idades dos animais. O modelo de regressão aleatória utilizado mostrou-se adequado para descrever as mudanças nas variâncias dos pesos de bovinos da raça Tabapuã do estado da Bahia.
Palavras- chave: bovino de corte, herdabilidade, modelo animal, seleção.

Abstract
In this study 28,643 weight records taken from birth to 660 days of age from 6,471 animals of the Tabapuã zebu breed were used to estimate (co)variance components and genetic parameters using a random regression model. The data were analyzed with the DFREML program applying the Restricted Maximum Likelihood method and using an AIREML algorithm. In the models, direct additive genetic, maternal, and permanent environmental (animal and maternal) effects were assumed to be random, contemporary groups were included as fixed effects, and the ages of animal at weighing and of dam at calving were used as covariables. Estimates of direct additive genetic variance increased with age. Heritability estimates for direct additive effect decreased from birth to weaning, whereas estimates of maternal heritability increased over this period and decreased at older ages. Direct genetic correlations ranged from moderate to high, so their magnitudes decreased with greater age gaps between animals. The random regression model used in this study was appropriate to describe changes in variance estimates for weights in Tabapuã cattle raised in the Brazilian state of Bahia.
Keywords: animal model, beef cattle, heritability, selection.

Recebido em: 23 de outubro de 2017.
Aceito em: 26 de outubro de 2018.

Introdução

O Brasil possui aproximadamente 208 milhões de cabeças de bovinos, sendo a pecuária bovina de corte uma atividade de fundamental importância no agronegócio, com PIB de aproximadamente 16 bilhões de dólares e envolvimento de 7 milhões de pessoas em toda a sua cadeia produtiva⁽¹⁾.

A produção bovina brasileira vem passando por um processo de modernização motivada pela necessidade de aumento da sua eficiência, visto que a introdução e a procura por outras carnes, além da exigência de produzir atendendo à sustentabilidade ambiental, ampliaram a competitividade do mercado⁽²⁾.

A região Nordeste é detentora de 28.245.689 animais, correspondendo a 13,4% do efetivo total brasileiro, ficando atrás em efetivo bovino das regiões Centro-Oeste, Norte e Sudeste⁽²⁾. Apesar do expressivo número de bovinos nesta região, a pecuária é baseada em animais zebuínos puros ou mestiços criados a pasto, apresentando índices produtivos baixos, o que pode ser devido à falta de programas de melhoramento abrangentes.

Segundo Bavia et al.⁽³⁾, o estado da Bahia contribui com 17,6% da produção de carne bovina do país e ocupa a sétima posição no ranking nacional, além de possuir o maior rebanho bovino da região Nordeste, destacando-se regional e nacionalmente pelo seu significativo efetivo de animais.

Os bovinos da raça Tabapuã são considerados como uma das melhores opções para produção de carne mais precoce, além disso, são animais que apresentam um excelente ganho em peso, extrema docilidade, fertilidade, precocidade reprodutiva, boa conformação e excelente habilidade materna⁽⁴⁾.

A modelagem de variáveis de crescimento visando à obtenção de valores genéticos e posterior seleção de animais pode ser realizada utilizando modelos de regressão aleatória. Os modelos de regressão aleatória (MRA) permitem a obtenção de curvas individuais de crescimento que consideram as variâncias genéticas e residuais ao longo do tempo, portanto, é possível a estimação de parâmetros genéticos e efeitos ambientais em cada uma das idades mensuradas, eliminando-se os pré-ajustes nos dados por trabalhar com todas as pesagens disponíveis, com covariâncias adequadas, mediante a determinação de coeficientes de regressão para esses efeitos⁽⁵⁾.

Nos últimos anos, as funções de covariâncias e os modelos de regressão aleatória têm sido propostos como uma alternativa para modelar características que são medidas repetidamente na vida dos animais, como o peso mensurado em diferentes idades⁽⁶⁾. Assim como também tem sido questionada nas últimas décadas a utilização de uma variável resposta de dimensão finita (por exemplo, peso vivo de um animal ajustado a uma idade-padrão) em comparação com as variáveis originalmente repetidas ao longo do tempo (dimensão infinita, por exemplo, pesos em diferentes idades), a partir da qual se estima a variável de dimensão finita⁽⁷⁾.

Assim, objetivou-se utilizar um modelo de regressão aleatória, ajustado por funções polinomiais de Legendre, para estimar os componentes de variância e covariância, utilizando-se a heterogeneidade de variância residual da curva de crescimento de bovinos da raça Tabapuã criados no estado da Bahia.

Material e métodos

Foram estudados pesos às várias idades considerados como medidas repetidas de um mesmo animal. Os dados foram obtidos junto à Associação Brasileira de Criadores de Zebu (ABCZ), referentes a animais da raça Tabapuã, nascidos no período de 1975 a 2001, criados no estado da Bahia. O arquivo inicial constava de 42.802 registros de pesos de 8.458 animais mensurados ao nascimento e, em média, a cada 90 dias, até os 660 dias de idade (ver Tabela 1).

A análise de consistência dos dados foi realizada via utilização do software SAS® (Statistical Analysis System, versão 9.1)⁽⁸⁾ e, após as devidas restrições, restaram 28.643 informações de pesagens para análise de regressão aleatória.

O grupo de contemporâneos (GC) foi composto por: sexo, mês e ano de nascimento, mês e ano de pesagem, fazenda e condição de criação (animais desmamados ou mamando sem ordenha).

Como a idade variou do nascimento até os 660 dias de idade, com idade a desmama de 220 dias de idade, o número de pesos de animais em cada dia de idade era bem reduzido no início e no fim das pesagens. Para corrigir isso e facilitar as avaliações dos dados, formaram-se classes de idades. Entretanto, a idade inicial, ou seja, a primeira idade não foi considerada, devido à grande variabilidade, portanto, a idade inicial foi datada a partir do quinto dia de vida, ou seja, a primeira classe de idade.

As idades seguintes foram formadas, tal como a inicial, a cada cinco dias, até 560 dias. Após essa idade, as classes foram agrupadas a cada 10 dias de idade, até os 630 dias, e então se agrupou a última classe em 30 dias, ou seja, 660 dias de idade, obtendo-se uma distribuição mais homogênea entre classes de idades. O resultado foi a formação de um total de 118 classes de idades

O modelo utilizado para analisar os dados de pesagens de animais da raça Tabapuã pela regressão aleatória foi o indicado como o mais adequado por Souza Junior et al.⁽⁶⁾. Portanto, para o modelo de regressão aleatória com ordens de 4, 5, 2, 3, para os efeitos genéticos aditivos direto e materno, ambiente permanente de animal e ambiente permanente materno respectivamente, sendo o resíduo modelado por função de variância de ordem quíntica.

O modelo geral pode ser representado por:

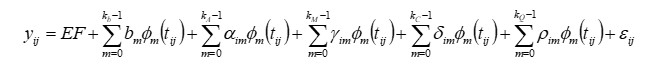
Onde:
y_ij = jésima medida do iésimo animal,
EF = conjunto de efeitos fixos,
bm = mésimo coeficiente de regressão do peso sobre a idade para a média da população (fixo),
α_im, ϒ_im, δ_im, ρ_im = mésimo coeficiente de regressão genético aditivo, genético materno e de ambiente permanente do animal e materno, respectivamente, para o iésimo animal (aleatório),
k_b, k_A, k_M, k_C e k_Q = ordem dos polinômios a serem ajustados,
t_ij = jésima idade do iésimo animal,
ϕ_m (t_ij) = mésima função polinomial a ser avaliada para a jésima idade do iésimo animal tij.
ε_ij = erro aleatório

As estimativas de herdabilidade (h²) e as correlações genéticas, fenotípicas e de ambiente entre as pesagens foram estimadas pelo modelo de regressão aleatória, utilizando as funções de covariância modelada pelo polinômio ortogonal de Legendre, proposto por⁽⁹⁾. Este modelo utilizou o algoritmo de busca⁽¹⁰⁾ através do método da máxima verossimilhança restrita pelo programa computacional DFREML 3.0β⁽¹¹⁾.

Em notação matricial, o modelo acima pode ser descrito como: Y= Xβ + Z₁α + Z₂ϒ +W₁δ + W₂ϒ + ε , e

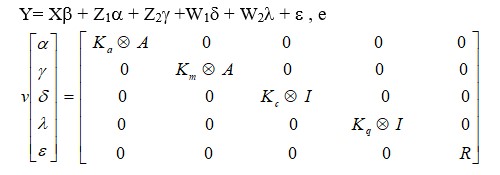
Onde:
Y é o vetor de observações;
β o vetor de efeitos fixos (incluindo Fij e βm);
α o vetor aleatório dos coeficientes genéticos aditivos diretos;
ϒ o vetor aleatório dos coeficientes genéticos aditivos maternos;
δ o vetor de coeficientes de ambiente permanente de animal;
λ o vetor de coeficiente de ambiente permanente materno;
X, Z₁, Z₂, W₁, W₂ são as matrizes de incidência correspondentes;
ε o vetor de resíduos;
K_a, K_m, K_c e K_q são as matrizes de variâncias e covariâncias entre os coeficientes de regressão aleatórios para os efeitos genéticos aditivos direto e materno e de ambiente permanente do animal e materno, respectivamente;
R é a matriz de variâncias residuais;
A é a matriz do numerador do coeficiente de parentesco aditivo;
I matriz identidade.

Para os modelos de regressão aleatória, utilizou-se a função dos polinômios ortogonais de Legendre(ϕk), representados da seguinte maneira:

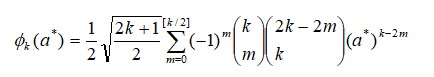
Onde:
a^* são as idades ajustadas para a amplitude em que o polinômio é definido [+1 a –1], e [ ] indica que os valores da fração são arredondados para baixo, assumindo o valor inteiro mais próximo.

Com relação ao resíduo, este foi modelado como homogêneo ou heterogêneo. Neste caso, foi utilizada função de variância residual quíntica, mantendo a ordem das funções de covariância para os efeitos genéticos direto (K_A) e materno (K_m) e ambiente permanente materno (K_q) e de animal (K_c) iguais a quatro (função de covariância cúbica).

A comparação entre os modelos foi realizada por meio do Critério de Informação Akaike (AIC) e do Critério de Informação Bayesiano de Schwarz (BIC), que permitem a comparação de modelos não aninhados e penaliza modelos mais parametrizados, sendo o BIC o mais rigoroso, ou seja, o que favorece modelos mais parcimoniosos⁽¹²⁾.

Os critérios AIC e BIC foram obtidos por: AIC = 2logL + 2p e BIC = 2logL + plog (N - r) em que: p é o número de parâmetros do modelo, N é o total de observações e r é o posto da matriz (matriz de incidência para os efeitos fixos). Menores valores de AIC e BIC e maiores para o Log L indicam modelos mais adequados.

A ordem do polinômio para cada efeito aleatório foi diminuída de acordo com as estimativas de variância dos coeficientes de regressão aleatória e os autovalores relacionados, pois baixas estimativas de variância e autovalores muito pequenos indicam pouca variação do determinado coeficiente.

Resultados e discussão

As análises descritivas para os dados analisados de massa corporal e as várias idades estão representadas na Figura 1, que apresentam o número de registros e as médias de pesos em kg. Pode-se observar uma maior concentração de registros nas idades iniciais da vida dos animais. As médias dos pesos aumentaram linearmente desde o nascimento até os 660 dias de idade, variando de 25 a 365 kg, respectivamente.

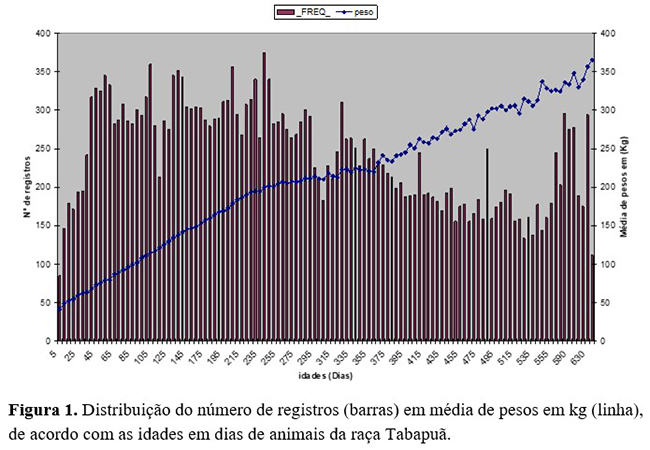
O peso apresentou aumento praticamente linear com a idade do animal até a desmama, mas, após esse período, houve pequena redução na taxa de ganho de peso. Os desvios-padrão também apresentaram tendência de aumento de acordo com a idade. Tanto as médias quanto os desvios-padrão aumentaram quase que linearmente com a idade do animal, apresentando uma diminuição da intensidade de crescimento após um ano de vida.

Portanto, observa-se uma tendência de o peso continuar aumentando até próximo aos dois anos de idade dos animais. Foram encontradas médias de pesos a desmama em bovinos Tabapuã no estado da Bahia de 212,80 kg, com valores semelhantes aos observados neste estudo⁽¹³⁾.

Resultados semelhantes foram encontrados por Oliveira et al.⁽⁴⁾, para a raça Tabapuã, utilizando modelos de regressão aleatória. Também observaram aumento linear do peso de acordo com a idade do animal até a desmama (em torno de 240 dias) e, após esse período, pequena redução na taxa de ganho de peso. O desvio-padrão também apresentou tendência de crescimento, variando de 3,55 kg ao nascimento a 57,25 kg aos 570 dias de idade.

Utilizando modelos estatísticos bayesianos⁽¹⁴⁾, encontraram-se resultados semelhantes a este estudo com aumento linear de peso do nascimento aos 660 dias de idade, variando de 31,40 Kg a 324,23 Kg, respectivamente. Assim como as médias de peso, os desvios-padrão também apresentaram tendência de aumento com a idade, e os coeficientes de variação aumentaram do nascimento até cerca de 50 dias. Após essa idade, houve reduzida diminuição do coeficiente de variação.

As estimativas de variância genética aditiva direta (Figura 2) obtidas aumentaram com a idade de 44 kg² a 52 kg² aos 79 dias de idade e 207 kg² a 264 kg² aos 550 dias de idade. Resultado similar foi observado por⁽⁴⁾, em estudo para estimação de parâmetros genéticos para peso do nascimento aos 660 dias de idade, para animais da raça Tabapuã, quando foi observado que, ao utilizar MRA, os valores aumentaram com a idade, de 22,58 kg² ao nascimento a 224,41 kg² aos 660 dias de idade.

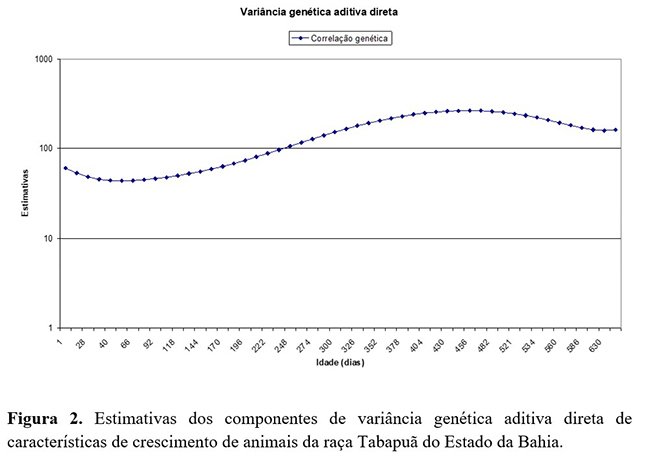
As estimativas de variância genética aditiva direta, e materna, e de ambiente permanente apresentaram tendência de crescimento à medida que aumentou a idade dos animais.

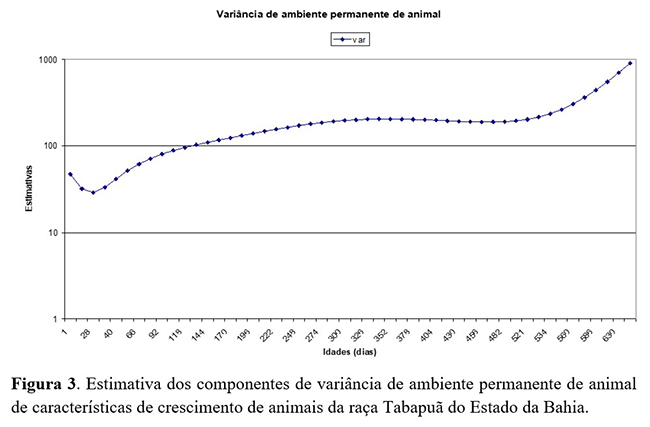
Nas estimativas de ambiente permanente de animal (Figura 3), observou-se o aumento das estimativas de variância em função da idade, sendo mais acentuado aos 550 dias de idade. Resultados com maiores magnitudes foram relatadas por Dias et al.(15), que obtiveram maiores aumentos das estimativas de variância em função da idade em animais da raça Tabapuã estudados até os 550 dias de idade. Esse aumento observado na variância de ambiente permanente de animal refletiu nas estimativas de variância fenotípica. A partição do efeito direto em genético e de ambiente permanente de animal nas análises de regressão aleatória, em geral, exige ordens maiores dos polinômios para esse efeito, o efeito de ambiente permanente de animal, e o que pode resultar em problemas de modelagem.

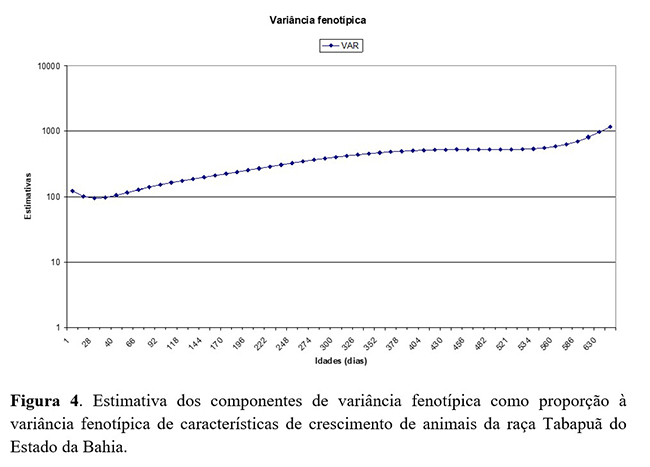
As estimativas de variância de ambiente permanente de animal (Figura 4), como proporção à variância fenotípica total, apresentaram leve queda do nascimento (0,31) até os 50 dias de idade (0,51) e, após essa idade, ocorre aumento, que se mantém até os 660 dias. Os resultados obtidos neste trabalho divergem dos obtidos por Oliveira et al.⁽⁴⁾ , que obtiveram leve aumento da variância de ambiente permanente de animal do nascimento aos 50 dias de idade e leve tendência de diminuição nas demais idades, diferindo-se deste trabalho após os 550 dias de idade, pois este estudo apresenta logo após a leve tendência de queda um crescimento à medida que aumenta a idade dos animais.

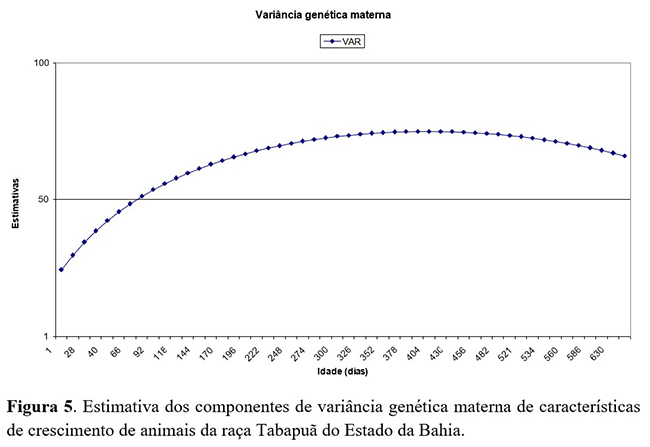
As estimativas de variância genética materna (Figura 5) aumentaram do nascimento (4,0 kg²) até próximo à época da desmama. Em seguida foi diminuindo, atingindo (26,6 kg2) aos 550 dias de idade. Comportamento semelhante foi descrito por Sousa Júnior et al.⁽¹⁴⁾, em análises com modelos de regressão aleatória na estimação de parâmetros genéticos para peso do nascimento aos 660 dias de idade para animais da raça Tabapuã.

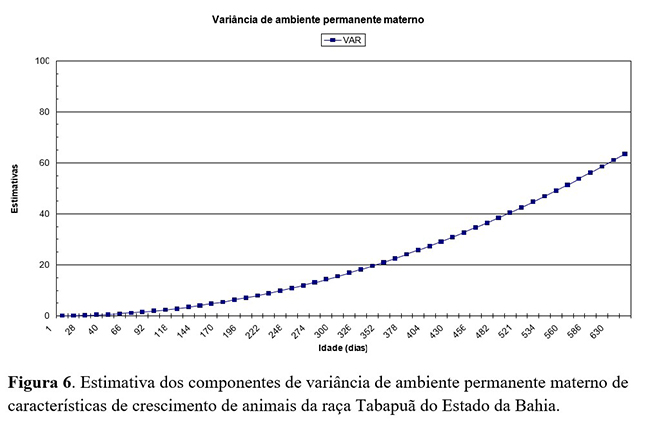
As estimativas de variância de ambiente permanente (Figura 6) apresentaram aumento progressivamente do nascimento (0,05 kg²) até os 660 dias de idade (63,5 kg²). Resultado semelhante ao descrito por Oliveira et al.⁽⁴⁾. Estimativas de variância de ambiente permanente materno como proporção da variância fenotípica total, obtidas por regressão aleatória, apresentaram um leve aumento com o passar da idade dos animais.

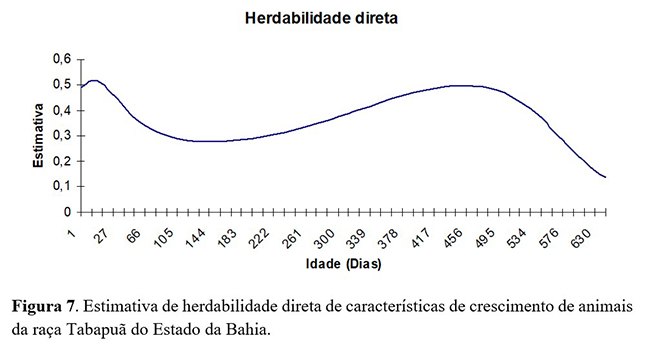
A herdabilidade para o efeito aditivo direto estimado em análise de regressão aleatória (Figura 7) mostra o decréscimo da herdabilidade do nascimento (0,48) até a desmama até (0,27). por volta dos 220 dias de idade e, após essa idade, apresentaram tendência de aumento até a idade de 495 dias (0,52). A partir dessa idade, houve decréscimo, atingindo 0,14 aos 660 dias de idade. Tal oscilação de um parâmetro genético é devido a cada idade ser controlada por pares de genes diferentes, tornando assim sua expressão diferente ao longo da vida dos animais.

Resultados semelhantes a este trabalho com modelo de regressão aleatória foram encontrados por Oliveira et al.⁽⁴⁾ , que descreveram diminuição das estimativas de herdabilidade após o nascimento e o aumento das estimativas após o período de desmame para peso de bovinos da raça Tabapuã. Estes autores observaram valores de herdabilidade direta de magnitude inferior aos encontrados nesta análise.

Resultados diferentes aos deste estudo em análises de regressão aleatória foram descritos por Sousa Júnior et al.⁽⁵⁾ com bovinos da raça Tabapuã, que encontraram estimativas de herdabilidade direta com pequena tendência de queda do nascimento (0,15) até os 20 dias (0,11) e, após essa idade, tenderam a aumento, atingindo 0,45 aos 660 dias de idade.

Em geral, as herdabilidades diretas estimadas e a variância genética aditiva direta sugerem haver variabilidade genética suficiente para a obtenção de ganho genético mais acentuado se a seleção individual for realizada considerando pesos após a desmama, uma vez que, nesse período, será possível melhor identificação dos animais geneticamente superiores.

As estimativas de herdabilidade materna em análise com modelo de regressão aleatória (Figura 8) apresentaram aumento do nascimento (0,38) até os 220 dias de idade (0,50), decrescendo nas idades seguintes a 0,17 até os 660 dias de idade.

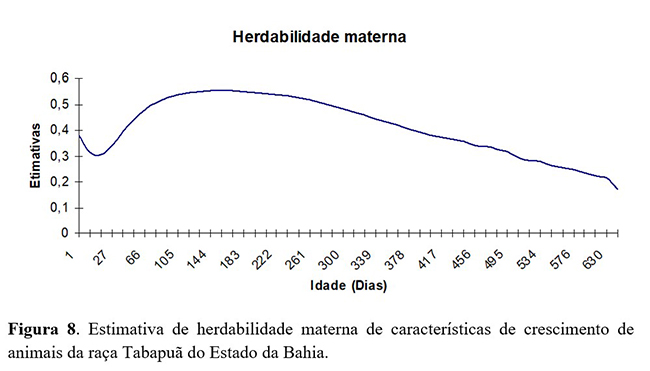
As maiores estimativas de herdabilidade materna coincidiram com o período em que as herdabilidades diretas apresentaram estimativas inferiores até os 500 dias de idade, período este em que a herdabilidade do efeito direto apresentou uma tendência de queda, talvez devido à convergência não totalmente alcançada para o modelo proposto. Os resultados obtidos com esta análise mostraram que os efeitos maternos começam a diminuir antes do período da desmama, o que pode ser devido ao desenvolvimento dos animais, sem a interferência das mães (vacas), o que ocorre de maneira mais drástica após os 220 dias de vida dos animais.

De acordo com Sousa Júnior et al.⁽⁵⁾ , os efeitos maternos afetam o peso, inclusive após o desmame. Provavelmente, pelo fato de que efeitos residuais permanecem após essa idade, afetando, portanto, o crescimento dos animais. Segundo Dias et al.⁽¹⁵⁾, a não inclusão dos efeitos maternos nos modelos de análise para peso a desmama ou a idade-padrão de 240 dias pode fazer com que parte da variância genética materna seja incluída na variância do efeito genético direto, resultando na superestimação desse efeito.

As correlações fenotípicas apresentaram diminuição conforme o distanciamento entre as diferentes idades são apresentadas na Tabela 2.

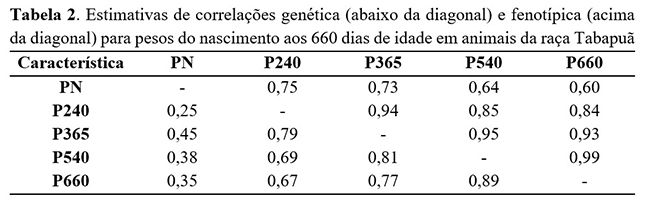
As correlações entre todas as idades e o peso ao nascimento foram baixas do nascimento até os 190 dias de idade. No entanto, a partir dessa idade, apresentaram altas magnitudes de 0,75, 0,73, 0,60, entre o peso ao nascer e peso aos 240 dias, entre o peso ao nascer e peso aos 365 dias e entre o peso ao nascer e peso aos 660 dias de idade. Tal resultado demonstra que, à medida que aumenta a distancia ente as idades, ocorre uma diminuição das magnitudes das correlações genéticas.

Resultado semelhante foi descrito por Dias et al.⁽¹⁵⁾ , que encontraram estimativas de correlações fenotípicas que diminuíram conforme as idades se distanciavam.

As estimativas de correlações fenotípicas entre os pesos nas idades-padrão (240, 365, 540 e 660 dias de idade) foram maiores, chegando a 0,94 no período de 240 e 365 dias de idade, a 0,85 entre 240 e 540 dias de idade a 0,84 entre 240 e 660 dias de idade. De acordo com Sousa Júnior et al.⁽⁵⁾, que também trabalharam com animais da raça Tabapuã, foram apresentadas altas magnitudes de correlações fenotípicas em animais do estado da Bahia.

As estimativas de correlação genética aditiva direta entre o peso ao nascimento e as demais idades foram, em geral, crescentes até em torno dos 230 e 255 dias de idades. A partir desse ponto diminuíram, com o aumento da distância entre as idades. As correlações entre o peso ao nascer e as idades-padrão foram moderadas, sendo 0,25; 0,45; 0,38 e 0,35 entre peso ao nascer e peso a desmama e 365, 540 a 660 dias de idade, respectivamente. As magnitudes das correlações genéticas e das herdabilidades encontradas neste trabalho indicam que é possível realizar uma seleção mais precoce de animais para pesos a idades posteriores, permitindo assim a realização de seleção de animais jovens da raça Tabapuã do estado da Bahia para fins de abate a idade adulta.

Resultados semelhantes foram observados por Oliveira et al.⁽⁴⁾ , que obtiveram estimativas de correlações genéticas estimadas entre o peso ao nascer e os pesos até os 365 dias de idade positivas, de moderadas a altas magnitudes, com tendência de diminuição após esse período. Portanto, a seleção com base nos pesos obtidos em idades jovens pode levar a aumento do peso ao nascimento, e a seleção para maiores pesos em qualquer idade deve alterar os demais pesos no mesmo sentido.

As correlações genéticas estimadas entre os pesos da desmama aos 660 dias de idade foram altas e positivas e indicam que a maior parte dos genes responsáveis por maiores pesos nesse período são os mesmos.

Para animais da raça Nelore⁽⁸⁾ , relataram-se correlações genéticas superiores entre pesos obtidos do nascimento aos 540 dias de idade. Estes mesmos autores descreveram correlações genéticas de 0,87 e 0,75 entre peso a desmama e peso aos 365 e 540 dias de idade, respectivamente, e 0,98 entre peso aos 365 e 540 dias de idade.

Conclusão

O modelo de regressão aleatória utilizado nesta análise mostrou-se adequado para descrever as mudanças que ocorreram nas variâncias para a curva de crescimento de bovinos, do nascimento aos 660 dias de idade, da raça Tabapuã, criados no estado da Bahia.

Os resultados obtidos indicam a possibilidade de alcançar maior resposta à seleção individual para os pesos após a desmama, haja vista que as estimativas de variância genética aditiva direta e de herdabilidade foram maiores nesse período. Isso possibilita uma melhor identificação dos animais geneticamente superiores.

As correlações genéticas obtidas no presente estudo sugerem que a seleção para maiores pesos em qualquer idade irá promover ganho nos pesos do nascimento aos 660 dias de idade.

Referências

1. IBGE, Instituto Brasileiro de Geografia e Estatística. Produção da pecuária municipal. v.38, p. 1-65, Rio de Janeiro, 2014. https://cidades.ibge.gov.br/xtras/home.php/Bahia. Acesso em out, 21, 2017.
2. Amaral RS, Carneiro PLS, Martins FILHO R, Ambrosini DP, Malhado CHM. Tendências, parâmetros fenotípicos e genéticos de características de crescimento em bovinos Nelore mocho do Nordeste brasileiro. Revista Brasileira de Saúde e Produção Animal. 2014; 15(2): 261-271. Disponível em: http://dx.doi.org/10.1590/S1519-99402014000200003.
3. Bavia ME, Carneiro DDMT, Cardim LL, Silva MMN, Martins MS. Estatística espacial de varredura na detecção de áreas de risco para a cisticercose bovina no estado da Bahia Arq. Bras. Med. Vet. Zootec.. 2012; 64(5):1200-1208. Disponível em: http://dx.doi.org/10.1590/S0102-09352012000500018.
4. Oliveira M R, Azevêdo DM, Malhado CH, Pires LC, Martins Filho R, Sousa Júnior SC. Weight evaluation of Tabapuã cattle raised in northeastern Brazil using random-regression models. Arq. Bras. Med. Vet. Zootec.. 2017; 69 (2):457-464. Disponível em: http://dx.doi.org/10.1590/1678-4162-9070.
5. Sousa Júnior SC, Oliveira SMP, Albuquerque LG, Boligon AA, Martins Filho R. Estimação de funções de covariância para características de crescimento da raça tabapuã utilizando modelos de regressão aleatória. Revista Brasileira de Zootecnia. 2010; 39 (5): 1037-1045. Disponível em: http://dx.doi.org/10.1590/S1516-35982010000500014.
6. Sousa Júnior SC, El Faro L, Bignardi AB, Cardoso VL, Machado PF, Lbuquerque LG. Aplicação de modelos de regressão aleatória utilizando diferentes estruturas de dados. Rev. Ciênc. Rural. 2014; 44 (2): 2058-2063. Disponível em: http://dx.doi.org/10.1590/0103-8478cr20131082.
7. Albuquerque LG, El Faro L. Comparações entre os valores genéticos para características de crescimento de bovinos da raça Nelore preditos com modelos de dimensão finita ou infinita. Revista Brasileira de Zootecnia. 2008; 37 (2): 238-246. Disponível em: http://dx.doi.org/10.1590/S1516-35982008000200009.
8. SAS Institute. Statistical Analysis System: user guide [CD-ROM]. Version 8. Cary (NC): SAS Insitute Inc., 2002.
9. Kirkpatrick M, Lofsvold D, Bulmer M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics. 1990; 124(4): 979 – 993. Disponível em: https://www.ncbi.nlm.nih.gov/pubmed/2323560.
10. Meyer K. An average information restricted maximum likelihood algorithm for estimating reduced rank genetic covariance matrices or covariance functions foranimal models with equal design matrices. Genet. Sel. Evol.. 1997; 29: 97-116. Disponível em: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2708219/pdf/1297-9686-29-2-97.pdf.
11. Meyer K. A program to estmate covariance fuctions for longitudinal data by REML. In: 6th. WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTIONS (VERSION β), Armidale, 1998. Disponível em: http://hal.archives-ouvertes.fr/hal-00894207.
12. Nuñez-Anton V, Zimmerman DL. Modeling nonstationary longitudinal data. Biometrics. 2000; 56: 699-705. Disponível em: DOI: http://dx.doi.org/10.1111/j.0006-341X.2000.00699.x.
13. Barbosa FA, Borges DN, Cabral Filho SLS, Graça DS, Andrade VJ, Souza CE. Leão JM, Mandarino RA. Desempenho de bovinos Tabapuã e seus cruzados em pastagens de braquiaria no Estado da Bahia. Arquivo Brasileiro de Medicina Veterinária e Zootecnina. 2014; 66 (1): 253-258. Disponível em: http://dx.doi.org/10.1590/S0102-09352014000100034.
14. Sousa Júnior S.C, Araújo Neto FR, Oliveira HN, Santos DO, Albuquerque LG, Rufino JES, Martins Filho R. Estimação bayesiana de componentes de (co) variância de características ponderais na raça tabapuã. Rev.Bras. Saúde Prod. An.. 2011; 12 (2): 350-358. Disponível em: http://revistas.ufba.br/index.php/rbspa/article/viewFile/2006/1105.
15. Dias LT, Albuquerque LG, Tonhati H, Teixeira RA. Estimação de parâmetros genéticos para peso do nascimento aos 550 dias de idade para animais da raça Tabapuã utilizando-se modelos de regressão aleatória. Revista Brasileira de Zootecnia. 2006; 35 (5): 1915-1925. Disponível em: http://dx.doi.org/10.1590/S1516-35982006000700006.