DOI: 10.1590/1089-6891v16i428131
PRODUÇÃO ANIMAL
COMPONENTS OF (CO)VARIANCE FOR AGE AT FIRST AND SECOND CALVING OF NELLORE FEMALES RAISED IN SOUTHERN BRAZIL
COMPONENTES DE (CO)VARIÂNCIA PARA IDADE AO PRIMEIRO E AO SEGUNDO PARTOS DE FÊMEAS DA RAÇA NELORE CRIADAS NO SUL DO BRASIL
Tiago Bresolin1*
Dionéia Magda Everling2
Camila Urbano Braz3
Fernanda Cristina Breda1
Paulo Roberto Nogara Rorato1
1 Universidade Federal de Santa Maria, UFSM, Santa Maria, RS, Brazil
2 Instituto Federal de Educação, Ciência e Tecnologia do Rio Grande do Sul, IFRS, Ibirubá, RS, Brazil
3 Faculdade de Ciências Agrárias e Veterinárias, UNESP, Jaboticabal, SP, Brazil
*Corresponding author: t_bresolin@zootecnista.com.br
The objective of this study was to estimate the heritability, genetic correlation and estimated breeding values for age at first (AFC) and second calving (ASC) for Nellore females raised in Southern Brazil. The (co)variance and estimated breeding values were obtained using Bayesian inference in a bivariate analysis, adopting an animal model. The average ages were 49.30 and 69.85 months, and the heritabilities were 0.25 and 0.26, respectively for AFC and ASC. The genetic correlation between AFC and ASC was 0.88. The correlation between the classifications of sires according to their estimated breeding values was 0.93. The heritability estimates for AFC and ASC suggest the possibility of obtaining genetic gain by selection. The correlation between these traits close to one indicates that they are controlled by virtually the same genes and when selected for one will advance correlated gain for the other.
Keywords: Bayesian inference; beef cattle; genetic parameters; fertility.
Este estudo teve como objetivo estimar os coeficientes de herdabilidade e predizer o valor genético dos reprodutores para idade ao primeiro (IPP) e ao segundo parto (ISP), além do coeficiente de correlação genética entre estas duas características, para fêmeas da raça Nelore, criadas no sul do Brasil. Os componentes de (co)variâncias, bem como os valores genéticos, foram obtidos através de Inferência Bayesiana, em análise bí-característica, adotando um modelo animal. As médias de idade foram 49,30 e 69,85 meses e os coeficientes de herdabilidade foram 0,25 e 0,26, respectivamente, para IPP e ISP. A estimativa de correlação genética entre IPP e ISP foi 0,88. A correlação da classificação dos touros, de acordo com seu valor genético, foi 0,93. As herdabilidades estimadas para IPP e ISP sugerem a possibilidade de obtenção de ganho genético pela seleção e a correlação entre estas características próximas de um indica que são controladas por praticamente o mesmo grupo de genes e que a seleção para uma delas promoverá ganho correlacionado para a outra.
Palavras-chave: bovinos de corte; fertilidade; inferência Bayesiana; parâmetros genéticos.
Recebido em: 02 fevereiro 2014
Aceito em: 03 junho 2015
Performance has been widely used as a selection criterion in breeding programs for beef cattle. However, in the last decade, some traits related to reproductive efficiency were incorporated to genetic evaluation programs. Age at first calving is the reproductive trait most widely used to assess the fertility of females.(1) An earlier age at first calving is related to the potential productive longevity of female, and is directly linked to efficiency and profitability of beef production.(2) The main advantages of calving at an earlier age are shorter time for return on investment, increase in the reproductive life of the cow, increase in the number of calves and reduction in the number of females in the herd.(3) Genetic gain by selection for sexual precocity is not a simple task, once that reproductive traits have low heritability;(4, 5) however, the age at first calving is easier to be measured(1) and does not imply in extra costs.(5) Low heritability estimates for age at first calving indicates that this trait is greatly influenced by environmental conditions. Some producers delay female reproduction by determining an age or weight in which the female start their reproductive life.(5) Furthermore, the use of short-term breeding seasons hinders early identification of sexually precocious females and many environmental factors are difficult to be considered in the analysis due to the lack of animal science records.(6) In the search for sexual precocity in females, several authors have studied the genetic correlation between age at first calving and other traits.(7-12)
Among the reproductive traits, calving interval may also be used as a selection criterion. However, Bourdon & Brinks(13) reported that using this trait for selection might not be an advantage due to the fact that selection for shorter intervals can induce indirect selection of animals born later in the calving season, and cows that calved at the end of the breeding season may have shorter intervals when compared to their counterparts, which calved at the beginning of the breeding season. Therefore, observing age at second calving can be an alternative to avoid using these animals as breeding stock. The use of age at first and second calving as a selection criterion is a low-cost procedure because all that is necessary is to record the date of calving. From the point of view of increasing reproductive efficiency of the herd, the information age at second delivery is extremely beneficial since it is related to puberty and female fertility. The objective of the present study was to estimate the heritability, genetic correlation and estimated breeding values of sires for age at first (AFC) and second calving (ASC) for Nellore females raised in Southern Brazil.
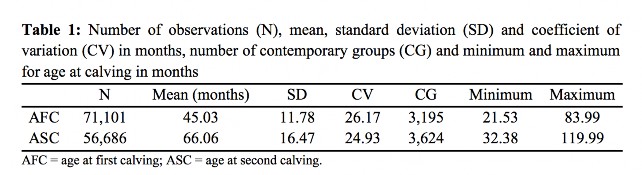
This study used 84,338 records of age at first and second calving of Nellore females, daughters of 55,186 dams and 6,241 sires, registered with the Brazilian Association of Zebu Breeders - ABCZ, raised in the states of Paraná, Santa Catarina and Rio Grande do Sul, and born from 1955 to 2010. The file was edited eliminating records for animals without genealogical information and cows without information for age at first (AFC) and second (ASC) calving. Contemporary groups (CG) for AFC (CG1) and ASC (CG2) were created for analyses, gathering females born in the same year, on the same farm and in the same state. Four birth season (BS) and calving seasons (CS) were established (fall, winter, spring and summer). The CGs with less than five observations were excluded. Descriptive statistics of the study population are shown in Table 1.

The model used for the data analysis included the fixed effects of CG and BS and CS, and as random the direct and residual additive genetic effects. The model can be described in matrix form as:
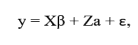
in which: y = vector of observations for each trait (AFC and ASC), X = incidence matrix for fixed effects (CG1, CG2, BS and CS), β = vector of fixed effects, Z = incidence matrix of the random additive genetic effect of each animal, a = vector of random additive genetic effects, and ε = is the vector of random residual effects.
The (co)variance components used to estimate the heritability and estimated breeding values were obtained by Bayesian inference, adopting a linear-linear animal model in bivariate analysis. To obtain estimates of the (co)variance and genetic parameters by Bayesian inference the GIBBS2F90 and POSTGIBBSF90(14) programs were used. In the context of Bayesian inference, a priori information about the parameters is used in association with the sample data by the function of likelihood, generating a posteriori joint distribution.(15-18) The full conditional distributions of genetic parameters were obtained from the joint of posteriori densities, i.e. the densities of the parameters, given the initial observations and information.
Chains of one million iterations without initial discarding and without sampling were generated with GIBBS2f90 program. A posteriori estimates were obtained using the POSTGIBBS program,(14) from which were discarded (burning) the first 100,000 iterations for heating Gibbs chains, in order to minimize the effects of the initial values. The discard period was by visual inspection of Gibbs chains, noting that from 100,000 iterations, they went into a constant, indicating the end of the heating period. The diagnosis of convergence was made using the BOA package(19) available in the R(20). The convergence of the Markov chain was verified through the criteria of Heidelberger & Welch(21), Geweke(22) and Raftery & Lewis.(23)
To ensure independent samples, a thinning interval of 160 was considered generating a total of 5,625 (co)variance component samples. Subsequently, by using the (co)variance samples heritability, genetic correlations and Monte Carlo error were calculated. The Monte Carlo error is the parameter estimation error by virtue of the number of samples used in Gibbs chain, which is calculated for each (co)variance component, by dividing this variance by number of samples. Therefore, the square root of this value is an approximation of the standard deviation of the error associated with the size of Gibbs chain.
The marginal distributions of the parameters obtained from the integration of a posteriori combined distribution, which provide the estimators (mean, mode and median) of interest were calculated using the program Gibanal.(24) The correlation between the ranking of estimated breeding values of bulls for both traits evaluated (AFC and ASC) were estimated by the Spearman Correlation by SAS.(25)
Using the program ACCF90,(14) the estimated accuracies were obtained through the relationship between the estimated and the real value of the parameter, which measure the degree removal of uncertainty associated with the value of EPD (Expected Progeny Difference) thereby, indicating the degree of trust in the EPD. The accuracy was obtained by the:
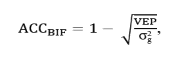
in which, VEP = variance of the prediction error, obtained from the
diagonal of the matrix C, intermediate matrix of the solving process of
the mixed-model equations and σg2 = true genetic variance.
This is an alternative formula adopted by the Beef Improvement Federation Guidelines(26) from the formula known as “Real Accuracy”, in which accuracy varies linearly with the number of progeny, resulting in lower and more conservative values of accuracy then those estimated by Real Accuracy.
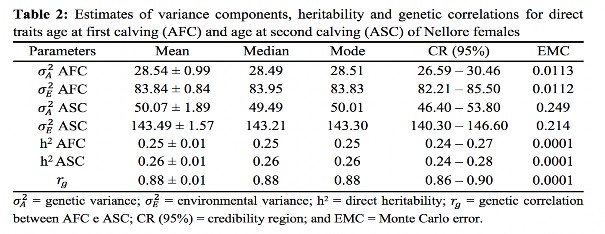
Average age at first calving (AFC) was higher than those reported by Pereira et al.,(27) Dias et al.,(5) Boligon et al.(9) and Silveira et al.,(28) respectively, equal to 35.67, 34.6, 36.21 and 41.83 months for Nellore females (Table 1). The variation of these averages may be due to different criteria for inclusion of animals in the evaluation of this trait, such as the upper limit established for AFC. Canchim dams Borba et al.(29) found an age of 54.32 months for the second calving. The estimated heritability for AFC (Table 2) was higher than the mean values reported by Pereira et al.,(27) Boligon et al.,(6) Boligon et al.(1) and Laureano et al.,(12) which ranged from 0.11 to 0.19, but was very close to the values reported by Mercadante et al.,(30) Gressler et al.(31) and Faria et al.,(11) which varied between 0.27 and 0.28.
Boligon et al.(6) pointed out that different models and samples cause disparity in the estimates of genetic parameters for reproductive traits. The trait AFC, for example, is dependent on the reproductive management adopted in different farms, which determines at which age females are exposed to reproduction. On the other hand, the effects included in the models, also cause changes in estimates. Other variables that affect the AFC and which are not always included in the analysis models, such as weight, body condition score, and feed, were not considered in this study. In assessments for AFC, only the females that have calved are part of the analysis, and therefore part of the variation in the trait is not able to be estimated. Thus, even using a fairly complete genealogy file, it is not often possible to obtain the actual genetic variability of the population.
According to Mercadante,(30) the reproduction traits normally recorded on the field include only females considered to be fertile. Thus, the samples are usually biased, which may contribute to mask the variability of the traits and genetic differences among animals. An alternative to minimize this problem would be to consider all females that were exposed to bulls or had the opportunity to conceive.
The heritability estimate for ASC (Table 2) was higher than those reported by Gressler et al.(31) for Nellore females and Baldi et al.(32) and Borba et al.(29), for Canchim cattle. The limited information available suggests that ASC presents variable heritability, although of lesser magnitude when compared to AFC, disagreeing with the values estimated in this study, suggesting the need for more studies on this parameter. However, the heritability found for AFC and ASC suggest that selection can be done for any feature.
The genetic correlation between ASC and AFC (Table 2) suggests most of the genes responsible for the expression of one of the traits are also responsible for the expression of the other, promoting correlated genetic gains. Thus, it is expected that if AFC is reduced, ASC will be reduced as well given the proper environmental conditions.
The Spearman correlation, considering the bulls contained in the database, was of high magnitude and significant level of p < 0.001. In Figure 1, the points circled in the lower diagonal identify sires that, although they are not among the first 1,000 to AFC, appear among the best for ASC; diagonally above are “plotted” the best sires for AFC but are not the best for ASC. So when one of these sires is used in a program that aims to reduce the age at first calving, genetic progress may not occur for age at second calving. If this difference in classification however small is neglected, it may result in the inappropriate choice of sires. The use of selection index may be an alternative to penalizing sires which, although may have good genetic value for AFC, are slower to reach ASC.
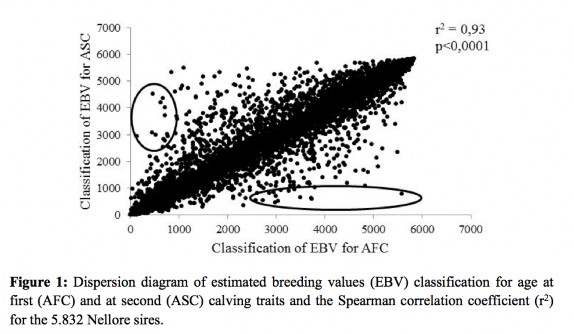
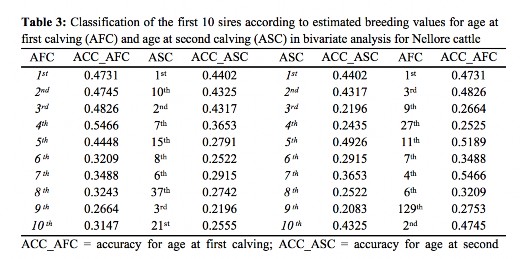
Sires best rated for ASC, but not for AFC probably have a lower calving interval. Several genetic and non-genetic factors can increase or decrease this period, it is difficult to separate these effects, since the recording of information which may affect this trait is not carried out in most farms, especially in extensive creations. When only the first ten sires are considered, there is practically no change in the classification (Table 3). The best sire for AFC is also the best for ASC and minor changes occurred in the other positions.
The age at first and second calving may be included in breeding programs, and should respond quickly to selection. The selection for age at first calving promotes genetic changes, in the same direction, for the age at second calving, and using any of these as selection criteria may produce genetic gain in the sexual precocity of females. Top rated sires for age at first calving are generally well classified for age at second calving.
1. Boligon AA, Albuquerque LG. Correlações genéticas entre escores visuais e
características reprodutivas em bovinos Nelore usando inferência
bayesiana. Pesquisa Agropecuária Brasileira. 2010;45(12):1412-1418.
2. Azevedo DMMR, Martins Filho R, Lôbo RNB, Malhado CHM, Lôbo RB, Moura AAA,
Pimenta Filho EC. Desempenho reprodutivo de vacas Nelore no Norte e
Nordeste do Brasil. Revista Brasileira de Zootecnia. 2006;35(3):988-996.
3. Short RY, Staimiller RB, Bellows RL, Greer RC. Breeding heifers at one
year of age: biological and economic considerations. In: Fieldes MJ, Sand
RS (Eds). Factors affecting calf crop. London: CRC Press;1994. p. 55-68.
English.
4. Pereira E, Eler JP, Ferraz JBS. Análise genética de características
reprodutivas na raça Nelore. Pesquisa Agropecuária Brasileira.
2002;37(5):703-708.
5. Dias LT, Lenira EF, Albuquerque LG. Estimativas de herdabilidade para
idade ao primeiro parto de novilhas da raça Nelore. Revista Brasileira de
Zootecnia. 2004;33(1):97-102.
6. Boligon AA, Vozzi PA, Nomelini J, Rorato PRN, Bezerra AF, Lôbo RB.
Parâmetros genéticos para idade ao primeiro parto estimados por diferentes
modelos para rebanhos da raça Nelore. Ciência Rural. 2008;38(2):432-436.
7. Silva JA II de V, Van Mellis MH, Eler JP, Ferraz JBS. Estimação de
parâmetros genéticos para probabilidade de prenhez aos 14 meses e altura
na garupa em bovinos da raça Nelore. Revista Brasileira de Zootecnia.
2003;32(5):1141-1146.
8. Bertazzo RP, Freita RTF, Gonçalves TM, Pereira IG, Eler JP, Ferraz JBS,
Oliveira AIG, Andrade IF. Parâmetros Genéticos de Longevidade e
Produtividade de Fêmeas da Raça Nelore. Revista Brasileira de Zootecnia.
2004;33(5):1118-1127.
9. Boligon AA, Rorato PRN, Albuquerque LG. Correlações genéticas entre
medidas de perímetro escrotal e características produtivas e reprodutivas
de fêmeas da raça Nelore. Revista Brasileira de Zootecnia.
2007;36(3):565-571.
10. Boligon AA, Albuquerque LG, Rorato PRN. Associações genéticas entre pesos
e características reprodutivas em rebanhos da raça Nelore. Revista
Brasileira de Zootecnia. 2008;37(4):596-601.
11. Faria CU, Magnobosco CU, Albuquerque LG, Reyes A de L, Bezerra LAF, Lôbo
RB. Abordagem bayesiana e freqüentista em análise genética tricaráter para
crescimento e reprodução de bovinos Nelore. Ciência Animal Brasileira.
2008;9(3):598-607.
12. Laureano MMM, Boligon AA, Costa RB, Forni S, Severo JLP, Albuquerque LG.
Estimativas de herdabilidade e tendências genéticas para características
de crescimento e reprodutivas em bovinos da raça Nelore. Arquivo
Brasileiro de Medicina Veterinária e Zootecnia. 2011;63(1):143-152.
13. Bourdon RM, Brinks JS. Calving date versus calving interval as a
reproductive measure in beef cattle. Journal of Animal Science.
1982;57(6):1412-1417.
14. Misztal I, Tsuruta S, Lourenco D , Aguilar I, Legarra A, Vitezica Z.
Manual for BLUPF90 family of programs. [S.l.], 2014. 125 p. Available
from: http://nce.ads.uga.edu.
English
15. Van Tassel CP, Van Vleck LD. Multiple-trait Gibbs sampler for animal
models: flexible programs for Bayesianand likelihood-based (co)variance
component inference. Journal of Animal Science. 1996;74(11):2586-2597.
16. Blasco A. The bayesian controversy in animal breeding. Journal of Animal
Science. 2001;79(8):2023-2046.
17. Guedes MHP, Muniz JA, Silva FF, Aquino LH. Análise bayesiana da curva de
crescimento de cordeiros da raça Santa Inês. Arquivo Brasileiro de
Medicina Veterinária e Zootecnia. 2005;57(3):415-417.
18. Mello SP, Alencar MM, Toral FLB, Gianlorenço VK. Estimativas de
parâmetros genéticos para características de crescimento e produtividade
em vacas da raça Canchim, utilizando-se inferência bayesiana. Revista
Brasileira de Zootecnia. 2006;35(1):92-97.
19. Smith BJ. Boa: An R Package for MCMC Output Convergence Assessment and
Posterior Inference. Journal Statistic Software. 2007;21(11):1–37.
20. R Core Team. R: A language and environment for statistical computing.
Vienna, Austria, 2013 [Cited 2013 May 20]. Available from: http://www.R-project.org.
English.
21. Heidelberger P, Welch PD. Simulation Run Length Control in the Presence
of an Initial Transient. Operations Research. 1983;31(6):1109-1144.
22. Geweke J. Evaluating the accuracy of sampling based approaches to the
calculation of posterior moments. In: Bernardo JM, Berger JO, David AP,
Smith AFM. (Eds). Bayesian statistics. New York:Oxford University; 1992.
p. 625–631. English.
23. Raftery AE, Lewis SM. Comment: one long run with diagnostics:
implementation strategies for Markov Chain Monte Carlo. Statistical
Science. 1992;7(4):493–497.
24. Van Kaan JBCHM. Gibanal 2.9: Analyzing Program for Markov Chain Monte
Carlo Sequences. Wageningen: Department of Animal Science / Agricultural
University, 1998.
25. SAS Institute. Statistical Analysis System: user guide [CD-ROM]. Version
9.3. Cary (NC): SAS Institute Inc., 2012.
26. Beef Improvement Federation - BIF. Guidelines for uniform beef
improvement programs. 8th ed. Manhattan: Kansas State University; 2006.
Available from:
http://beefimprovement.org/library/06guidelines.pdf. English.
27. Pereira E, Eler JP, Ferraz JBS. Correlação genética entre perímetro
escrotal e algumas características reprodutivas na raça Nelore. Revista
Brasileira de Zootecnia. 2000;29(6):1676-1683.
28. Silveira JC, Macmanus C, Mascioli AS, Silva LOC, Silveira AC, Garcia JAS,
Louvandini H. Fatores ambientais e parâmetros genéticos para
características produtivas e reprodutivas em um rebanho Nelore no estado
do Mato Grosso do Sul. Revista Brasileira de Zootecnia.
2004;33(6):1432-1444.
29. Borba LHF, Baldi F, Silva LOC, Boligon AA, Alencar MM. Parâmetros
genéticos para características de crescimento e reprodução de bovinos da
raça Canchim. Pesquisa Agropecuária Brasileira. 2011;46(11):1570-1578.
30. Mercadante MEZ, Lôbo RB, Oliveira HN. Estimativas de (co)variâncias entre
características de reprodução e de crescimento em fêmeas de um rebanho
Nelore. Revista Brasileira de Zootecnia. 2000;29(4):997-1004.
31. Gressler MGM, Pereira JCC, Bergmann JAG, Andrade VJ, Paulino MF, Gressler
SL. Aspectos genéticos do peso à desmama e de algumas características
reprodutivas de fêmeas Nelore. Arquivo Brasileiro de Medicina Veterinária
e Zootecnia. 2005;57(4):533-538.
32. Baldi F, Alencar MM, Freitas AR, Barbosa RT. Parâmetros genéticos para características de tamanho e condição corporal, eficiência reprodutiva e longevidade em fêmeas da raça Canchim. Revista Brasileira de Zootecnia. 2008;37(2):247-253.