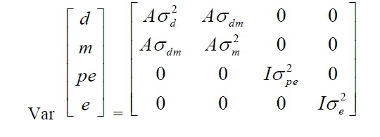
EFFECT OF SEVERAL STRUCTURES OF CONTEMPORARY GROUPS ON ESTIMATES OF (CO)VARIANCE AND GENETIC PARAMETERS FOR WEANING WEIGHT IN NELLORE CATTLE

Lillian Pascoa¹, Arcadio de los Reyes², Mauricio A. Elzo³, Jorge Luiz Ferreira⁴, Luiz A.F. Bezerra⁵, Raysildo Barbosa Lobo⁵

ABSTRACT

We used actual and adjusted weights to 120 d and 210 d of age of 72,731 male and female Nellore calves born in 40 PMGRN - Nellore Brazil herds from 1985 to 2005 aiming to compare the effect of different definitions of contemporary groups on estimates  of (co)variance and genetic parameters. Four models, each one with a different structure of contemporary group (CG), were compared using the Akaike Information Criterion (AIC), the Bayesian Information Criterion (BIC), and the Consistent Akaike Information Criterion (CAIC). (Co)variance estimates were obtained using a derivative-free restricted maximum likelihood procedure. Estimates of (co)variances and genetic parameters were similar for the four models considered. However, the BIC and CAIC indicated that the most appropriate model for this Nellore population was the one that considered CG to be random, and sex of calf to be fixed and separate from CG, in which CG was defined as the group of calves born in the same herd, year, season of birth (trimester), and undergone the same management.
--------------------
 KEYWORDS: beef cattle; contemporary groups; information criteria.

EFEITO DE DIFERENTES MODELOS SOBRE AS ESTIMATIVAS DE (CO)VARIÂNCIAS E PARÂMETROS GENÉTICOS PARA PESOS ATÉ A DESMAMA EM GADO NELORE

RESUMO

---------------------
PALAVRAS-CHAVE: critérios de informação; gado de corte; grupos contemporâneos.

INTRODUCTION

The structure of contemporary groups (CG) is of primary importance for genetic evaluation of animals under selection; they are crucial to avoid potential biases in genetic evaluations due to differential treatment of animals in a population (VAN VLECK, 1987).

Contemporary groups have usually been considered as fixed effects in beef cattle genetic evaluations. This has been based on HENDERSON (1973) statement that in sire models, genetic predictions of sires would be associated to contemporary group effects, and to eliminate this bias, CG needed to be defined as fixed effects. Currently, the model of choice is an animal model where individuals are assumed to represent a random sample of the genetic material in a population; however, CG continues to be considered as fixed effects.

Some authors have found that random CG effects yield a better adjustment than models with fixed CG in various animal species. In small herds, BABOT et al. (2003) managed to estimate genetic values for litter size in herds with insufficient number of animals per CG using simulated data, whereas VASCONCELOS et al. (2005) estimated genetic values for milk production in dairy cattle in Portugal using contrast models. Treating CG as random effects was also found to be advantageous by GONZÁLEZ-RECIO & ALENDA (2005) when analyzing binary reproductive traits in Spanish dairy cattle, by WOLF et al. (2005) for growth and litter size in swine utilizing a multi-trait animal model, and by LEGARRA et al. (2005) for milk production in ewes using a Bayesian approach.

To obtain the best possible estimates of (co)variance and genetic parameters it is important to define mathematical models that fit the available data as accurately as possible. This will in turn yield the most accurate genetic predictions given the available information. Thus, the objective of this study was to compare models with different definitions of contemporary groups on estimates of (co)variances and genetic parameters for actual and adjusted weights at 120 and 210 d of age in Nellore cattle in Brazil.

MATERIAL AND METHODS

 
Actual and adjusted weights at 120 d (AW120, RW120) and 210 d (AW210, RW210) from 72,731 male and female Nellore calves born between 1985 and 2005 in 40 herds from PMGRN-Nellore Brazil were used in this study. Actual weights were the closest ones to 120 d and 210 d within the intervals of 120 ± 90 d and 210 ± 90 d, respectively. Calf ages were expressed as deviations (CAD) from 120 d and 210 d. Adjusted weights were computed by interpolation between a prior and a posterior weight to the standardized age (120 d or 210 d), allowing a maximum interval of 195 d between these two weights (± 90 d plus an additional 15 d due to possible management changes). Birth weight was used as the prior weight for AW120 when there was no other weight (actual birth weight or breed mean: 33 kg for males, and 31 kg for females) to compute the interpolation. Computations were similar to PMGRN (LÔBO, 1996):

 AW = W + [(W-Wp)/I] x (A - Aw)

 where, AW = adjusted weights at standard ages (AW120 or AW210); W = actual weight; Wp = prior weight; I = interval in days between W and Wp; A = standard age (120 d or  210 d);  Aw = age at measurement of W.

The effect of age of cow in years was grouped into six classes (DAC): 1 = 2 yr; 2 = 3 yr; 3 = 4 yr; 4 = 5 yr; 5 = 6 to 9 yr; and 6 = 10 yr and older cows.

Four structures of contemporary groups were defined by concatenation of individual effects, starting from a base subclass (CG_B), as follows:

CG_B: herd – year of birth – management group at each age.

CG₁: CG_B – semester of birth.

CG₂: CG_B – trimester of birth.

CG₃: CG₁ – sex of calf.

CG₄: CG₂ - sex of calf.

Based on these four CGs (CG₁ to CG₄), four analytical models were defined:

M₁: Weight = α + CG₁ + SC + DAC + ε

M₂: Weight = α + CG₂ + SC + DAC + ε

M₃: Weight = α + CG₃ + DAC + ε

M₄: Weight = α + CG₄ + DAC + ε

where, Weight = actual or adjusted weight at 120 d or 210 d of age; α = constant; CG = contemporary group; SC = sex of calf; DAC = class of cow age at calving, and ε = random residual effect. In addition, models for actual weights included age of calf at weighing (CAD), modeled as a cubic polynomial regression, and expressed as a deviation from 120 d or 210 d.
A minimum of five observations per contemporary groups were required. Calves in CG with less than five observations were kept in the database but their weights were set to zero, thus their genetic evaluations were computed using solely information from their relatives. This allowed us to have the same inverse of the relationship matrix (A^-1) with 119,586 animals in all analyses.

Models for the estimation of (co)variances and genetic parameters for AW120, RW120, AW210 e RW210 using single-trait analysis, considering CG fixed (1) or random (2), were as follows:

y = Xb + Z₁d + Z₂m + Z₃pe + e                                    (1)

y = Xb + Z₁d + Z₂m + Z₃pe + Z₄c + e               (2)

where, y = vector of observations; b = vector of fixed effects, including CG (Equation 1), and the effects of SC, DAC, and a cubic polynomial regression on CAD for the analysis of actual weights (Equations 1 and 2); d, m, pe, c and e = vectors of additive direct genetic effects, additive maternal genetic effects, maternal permanent environmental effects, contemporary group, and residual, respectively; and X, Z₁, Z₂, Z₃ e Z₄, are known incidence matrices relating observations in vector y to vectors b, d, m, pe, and c, respectively.  The assumptions of these models were:

 E[y] = Xb, and E[d] = E[m] = E[pe] = E[c] = E[e] = 0

and

for model 1, and

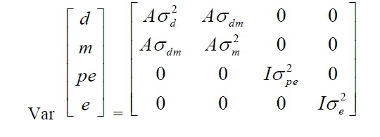
for model 2, where, A = matrix of additive relationships among individuals; I = identity matrices of appropriate order, σ²_d, σ²_m, σ²_pe, σ²_c  and σ²_e = additive direct genetic variance, additive maternal genetic variance, permanent environmental variance, contemporary group variance, and residual variance, respectively; and σ_dm= covariance between direct and maternal genetic effects.

Models were compared using the logarithm of the likelihood function (logL), using the Akaike Information Criterion (AIC; AKAIKE, 1972), the Bayesian Information Criterion (BIC; SCHWARZ, 1978), and Consistent Akaike Information Criterion (CAIC, BOZDOGAN, 1987). The CAIC gives higher penalties to hyperparametrized models compared to AIC. Thus, BIC and CAIC favor parsimonious models. These criteria are defined as follows:

AIC = -2logL + 2k

BIC = -2logL + klog(n)

CAIC = -2logL + k(log(n)+1)

where, k = number of estimated parameters; n = number of observations; logL = logarithm of the likelihood function.

Models with lower values of these information criteria are considered to better fit the data.

Estimates of (co)variances and genetic parameters were obtained using a derivative-free restricted maximum likelihood procedure (DFREML; SMITH & GRASER, 1986). Computations were carried out using the MTDFREML (Multiple Trait Derivative Free Restricted Maximum Likelihood; BOLDMAN et al., 1995) software package using a single-trait animal model. Because comparisons among animals were done within contemporary groups, the variance due to CG, in those models that considered CG to be random, was not included in the phenotypic variance.

RESULTS AND DISCUSSION

Model Fitting

Values for the information criteria AIC, BIC and CAIC obtained using models 1 through 4 with CG either fixed or random are presented in Table 1 for 120 d and in Table 2 for 210 d of age. By any of these criteria, better fitting models have smaller values.

In all cases, the criterion AIC had the smallest values for models with CG fixed. On the other hand, BIC and CAIC, by imposing higher penalties than AIC for models with higher number of estimated parameters, favored models with random CG. These results were in agreement with results from the literature. UGARTE et al. (1991), working with simulated data, and VISSHER & GODDARD (1992), working with dairy data from small herds, estimated lower prediction error variances (PEV) and mean squared errors (MSE) for models with random CG. Contrarily, VALVERDE et al. (2008), using Braunvieh cattle weaning weight data, found somewhat higher accuracies of genetic predictions for direct genetic effects when CG were considered fixed, and no difference between models with CG fixed or random for maternal genetic effects.

For weights at 120 d (AW120 and RW120), the criteria BIC and CAIC indicated that models with trimester seasonal effect had the best fit when CG was random (Table 1). A similar result was obtained for weights at 210 d (AW210 and RW210; Table 2). However, when CG was fixed, the best fitting models were those with semester seasonal effects for 120 d (AW120 and RW120), whereas for weights at 210 d, model M₂ (trimester) was better than M₁ (semester), but model M₃ (semester) was better than M₄ (trimester) for AW210 and RW210. On the other hand, REYES et al. (1998) found out that it was better to consider trimester over semester when they compared the efficiency of two fixed effects models containing season (trimester or semester) as part of the structure of contemporary groups for weaning weight in Nellore cattle.

According to the BIC and CAIC criteria, models that had sex of calf effect separated from CG, provided a better fit to the data. These models allowed the construction of contemporary groups with larger number of individuals and permitted better genetic connections among CG and higher accuracies of prediction of genetic evaluations. These results are in agreement with those found by REYES et al. (2006) for growth between birth and weaning in a multibreed Nellore x Hereford cattle population.

Among models with random CG, model M₂ was the most parsimonious and provided the best fit. Thus, for 120 d and 210 d of age and actual or adjusted data, results here suggest that models that had random CG with trimester seasonal effect, and sex of calf effect separated from CG effect were the most appropriate for growth from birth to weaning in Nellore cattle.

 (Co)variance components and genetic parameters

Tables 3 and 4 present the estimates of (co)variances and genetic parameters for the four traits in this study (AW120, RW120, AW210 e RW210). Estimates for each trait differed little among models.

Estimates of σ²_d, σ²_m, h²_d  and h²_m were larger in models with semester of birth season effect in CG (M₁ and M₃) than those obtained in models with trimester of birth season effect in CG (M₂ e M₄). On the other hand, estimates of σ²_pe and σ²_e were similar in all models. These results may have been due to greater variation among weights when the period of time (season effect) considered in CG was longer.

Estimates of σ²_d, σ²_m, h²_d and h²_m  for weight at 120 d and 210 d of age were similar in models that included or not the effect of sex of calf within CG (M₂ vs M₄ and M₁ vs M₃). Estimates of σ²_e ranged from 118.61 to 163.01 kg² for actual and adjusted weights at 120 d (W120), and from 223.99 to 292.43 kg² for actual and adjusted weights at 210 d (W210), with smaller values in CG of larger size, i.e., those in models that considered semester seasonal effects and sex of calf separately from CG.

Models that considered CG random yielded higher estimates of σ²_d, σ²_m, h²_d and h²_m  , and lower estimates of σ²_e than models that considered CG fixed. Larger estimates of σ²_d and smaller values of σ²_e in models with random CG were also obtained for weaning weights in Braunvieh cattle in México (VALVERDE et al., 2008). Literature values reported higher values of heritability estimates for models with fixed CG than for models with random CG (PHOCAS & LALOE, 2003; CHANVIJIT et al., 2005; VALVERDE et al., 2008). However, these lower heritability estimates for models with random CG were computed with phenotypic variances that included the variance due to contemporary group (σ²_c), which is not appropriate because comparisons among animals evaluated genetically occur within contemporary groups.

Estimates for σ²_d ranged from 56.20 to 68.17 kg² and estimates for σ²_m from 24.86 to 29.67 kg² for weight at 120 d of age (W120). For weights at 210 d of age (W210), σ²_d estimates ranged from 116.61 to 155.44 kg² and estimates of σ²_m ranged from 41.91 to 52.05 kg². Estimates of σ²_dm were negative, ranging from -38.61 to -20.84 kg² for W120 and from     -38.94 to -21.41 kg² for W210. These estimates indicated antagonism between additive direct and maternal genetic effects, in agreement with previous beef cattle research (FERREIRA et al., 1999; LEE & POLLAK, 2002; ROSALES et al., 2004). This implies that if producers perform selection for growth in calves without considering maternal additive genetic effects, this may produce a decrease in milk production of future mothers and a reduction in weaning weights of their progenies (VALVERDE et al., 2008).

Estimates of σ²_pe ranged from 30.38 to 33.97 kg² for W120 and from 66.59 to 74.27 kg² for W210. These estimates were higher than those reported by GARNERO et al. (2001) for weights at 120 d of age (19.1 kg²) and at 220 d of age (48.01 kg²).

Direct heritability estimates ranged from 0.22 to 0.28 for W120 and from 0.25 to 0.32 for W210. Estimates of maternal heritabilities ranged from 0.10 to 0.12 for W120 and from 0.09 to 0.11 for W210. MARCONDES et al. (2002) and SIQUEIRA et al. (2003) found similar estimates of direct heritability for W120 (0.24 and 0.29, respectively), and of maternal heritability (0.08) in Nellore cattle. GARNERO et al. (2001) also estimated values of heritability for direct genetic effects (0.19) and for maternal genetic effects (0.06) similar to those obtained here.

Differences among estimates of (co)variances and genetic parameters were small across models in this study, perhaps due to the utilization of the same matrix of additive relationships. However, one could expect that estimates from models that yield better fit would be more accurate and reliable.

 
CONCLUSIONS

 The most appropriate model for the estimation of (co)variances and genetic parameters for actual and adjusted weights at 120 d and 210 d of age in Brazilian Nellore cattle was the one that had random CG and sex of calf separated from CG, where CG was defined as a group of calves born in the same herd, year, season measured as trimester of birth, and had the same management. Estimates of (co)variances and genetic parameters, predictions of breeding values, and ranking of animals obtained with the best model are expected to be more accurate and reliable.

 
REFERENCES

AKAIKE, H. Information theory and an extension of maximum likelihood principle. In: INTERNATIONAL SYMPOSIUM ON INFORMATION THEORY, 2., Proceedings… p.267-281, 1972. Disponível em http://www.sortiend.org/lme/Statistical%20Papers/Akaike_1973%20with%20commentary.pdf, acesso em 03 de março de 2013.

BABOT, D.; NOGUERA, J.L.; ALFONSO, L.; ESTANY, J. Fixed or random contemporary groups in genetic evaluation for litter size in pigs using a single trait repeatability animal model. Journal of Animal Breeding and Genetics, v. 120, n. 1, p.12-22, 2003.

BOLDMAN, K.; KRIESE, L.; VAN VLECK, L.D. A manual for use of MTDFREML : A set of programs to obtain estimates of variances and covariances. USDA. ARS., 1993.

BOZDOGAN, H. Model selection and Akaike’s information criterion (AIC): the general theory and its analytical extensions. Psychometrika, v. 52, p.345-370, 1987.

CHANVIJIT, K.; DUANGJINDA, M.; PATTARAJINDA, V.; REODECHA, C. Model comparison for genetic evaluation of Milk yield in crossbred Holsteins in the tropics. Journal of Applied Genetics, v. 46, n. 4, p.387-393, 2005.

FERREIRA, G.B.; MACNEIL, M.D.; VAN VLECK, L.D. Variance components and breeding values for growth traits from different statistical models. Journal of Animal Science, v. 77, p. 2641-2650, 1999.

GARNERO, A.V.; LOBO, R.B.; BEZERRA, L.A.F.; OLIVEIRA, H.N. Comparação entre alguns critérios de seleção para crescimento na raça Nelore. Revista Brasileira de Zootecnia, v.30, n. 3, p.714-718, 2001.

GONZÁLEZ-RECIO, O.; ALENDA, R. Genetic parameters for female fertility traits and a fertility index in Spanish dairy cattle. Journal of Dairy Science, v. 88, p. 3282-3289, 2005.

HENDERSON, C.R. Sire evaluation and genetics trends. In: ANIMAL BREEDING AND GENETIC SYMPOSIUM IN HONOR OF DR. JAY L. LUSH, Illinois, USA. Proceedings… Illinois, v. 1, p.10-41, 1973. Disponível em: <http://jas.fass.org/cgi/reprint/1973/Symposium/10> Acesso em: 15 mar. 2011.

LEE, C.; POLLAK, E.J. Genetic antagonism between body weight and milk production in beef cattle. Journal of Animal Science, v. 80, p.316-32, 2002.

LEGARRA, A.; LÓPEZ-ROMERO, P.; UGARTE, E. Bayesian model selection of contemporary groups for BLUP genetic evaluation in Latxa dairy sheep. Livestock Production Science, v. 93, p.205-212, 2005.

LÔBO, R.B. Programa de Melhoramento Genético da Raça Nelore, 2 Ed. Ribeirão Preto, SP: ANCP, 1996.

MARCONDES, C.R.; GAVIO, D.; BITTENCOURT, T.C.C.; LÔBO, R.B.; BEZERRA, L.A.F.; TONHATI, H. Estudo de modelo alternativo para estimação de componentes de (co)variância e predição de valores genéticos de características de crescimento de bovinos da raça Nelore. Arquivo Brasileiro de Medicina Veterinária e Zootecnia, v. 54, n. 1, p. 93-99, 2002.

PHOCAS, F.; LALOË, D. Evaluation models and genetic parameters for calving difficulty in beef cattle. Journal of Animal Science, v. 81, p.933-938, 2003.

REYES, A.; LOBO, R.B.; BEZERRA, L.A.F.; MARTINS, E.N. Critérios de época na conformação de grupos contemporâneos para características de crescimento em Nelore. In: REUNIÃO ANUAL DE SOCIEDADE BRASILEIRA DE ZOOTECNIA, 35., Botucatu. Anais... Botucatu : SBZ, v. 3, n. 1, p. 437-439, 1998. Disponível em http://www.sbz.org.br/reuniaoanual/anais/arq_reuniao_anual/sbz1998.rar. Acesso em 03 março 2013.

REYES, A.; ELZO, M.A.; ROSO, V.M.; FRIES, L.A.; CARVALHEIRO, R. Efeitos não genéticos na composição dos grupos contemporâneos para o ganho de peso do nascimento a desmama de uma população multirracial Nellore x Hereford. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 43., João Pessoa. Anais... João Pessoa, 2006. Disponível em: <http://www.animal.ufl.edu/elzo/Publications/Proceedings/2006/Sociedad%20Brazileira%20de%20Zootecnia/Reyes%20et%20al._
SBZ43_July-24-27-2006_Trabalho_HOMEPAGE.pdf. Acesso em 20 out. 2009.

ROSALES, A.J.; ELZO, M.A.; MONTANO, B.M. Parámetros y tendencias genéticas para características de crecimiento predestete em la población mexicana de Simmental. Revista Mexicana de Ciencias Pecuarias, v. 42, p. 171-180, 2004.

SCHWARZ, G. Estimating the dimension of a model. The Annals of Statistics, v. 6, n. 2, p.461-464, 1978. Disponível em: < http://www.jstor.org/stable/2958889> Acesso em: 15 mar. 2011.

SIQUEIRA, R.L.P.G.; OLIVEIRA, J.A.; LOBO, R.B.; BEZERRA, L.A.F.; TONHATI, H. Análise da variabilidade genética aditiva de características de crescimento na raça Nelore. Revista Brasileira de Zootecnia, v. 32, n. 4, p. 880-886, 2003.

SMITH, S.P.; GRASER, H.U. Estimating Variance Components in a Class of Mixed Models by Restricted Maximum Likelihood. Journal of Dairy Science, v. 69, p. 1156-1165, 1986.

UGARTE, E.; ALENDA, R.; CARABAÑO, M.J. Fixed or random contemporary groups in genetic evaluations. Journal of Dairy Science, v. 75, p. 269-278, 1991.

VALVERDE, R.R.; DOMÍNGUEZ, R.N.; FLORES, A.R.; MUÑÍS, J.G.G.; VALENCIA, F.M. Comparación de definiciones de grupos contemporáneos en la evaluación genética de bovinos Suizo Europeo. Revista Mexicana de Ciencias Pecuarias, v. 46, n. 4, p. 359-370, 2008.

VAN VLECK, L.D. Contemporary Groups for Genetic Evaluations. Journal of Dairy Science, v. 70, p. 2456-2464, 1987.

VASCONCELOS, J.; MARTINS, A.; FERREIRA, A.; CARVALHEIRA, J. Consequências da eliminação de rebanhos pequenos da avaliação genética de bovinos leiteiros em Portugal. Revista Portuguesa de Zootecnia, v. 12, p. 105-117, 2005.

VISSHER, P.M.; GODDARD, M.E. Fixed and random contemporary groups. Journal of Dairy Science, v. 76, p. 1444-1454, 1992.

WOLF, J.; ZAKOVA, E.; GROENEVELD, E. Genetic parameters for a joint genetic evaluation of production and reproduction traits in pigs. Czech Journal of Animal Science, v. 50, n. 3, p. 96-103, 2005.

 Protocolado em: 17 mar. 2011.   Aceito em 05 mar. 2013