

Revista Música Hodie, Goiânia - V.14, 269p., n.2, 2014
Eduardo Solá (University of Toronto, Faculty of Music, Toronto, Canadá)
Keywords: Violin; Marco Uccellini; Seventeenth (17th) century; Metrical dissonance; Rule of Down-Bow; Musical notation.
A Sonata Ottava op. 4, de Marco Uccellini: Perpectivas em Agrupamento, Métrica e Dissonância Métrica
The present study aims at exploring how the early-seventeenth-century violinist may have perceived and interpreted meter in a particularly challenging repertoire and its problematic issues to do with tempo and rhythm. Marco Uccellini’s Sonata ottava a Violino e Basso, from his op. 4 (1645), will be used here to exemplify the way in which these prob- lems come into existence, being even more salient to the modern musician, and how some practical historical guidelines offer a unique alternative to performing metrical stress. The absence of bar lines in Italian instrumental works in the first half of the century required an alternative way of perceiving local metrical units that essentially differs from the ones available today. The current tendency to inevitably analyze and interpret this repertoire with modern eyes, even in a “historically informed” approach, has doubtlessly interfered in the way we understand it. To be sure the advent and establishment of the bar line in music notation is a significant landmark in the realm of metrical perception and performance, but not the only system. Although it eventually replaced the mensural legacy from several past centuries, both notational systems still coexisted throughout the theoretical limbo the be- ginning of the seventeenth century eventually became.
As a general proposition this study will focus on a contextual approach to this repertoire, taking into consideration the substantial lack of bar lines found in some of these works and drawing upon treatises and performing instructions from authors active around the time and place where Uccellini wrote his op. 4, no. 8. However, especially be- cause it was conceived at a time when a clear theory of rhythm and meter could not be
Revista Música Hodie, Goiânia - V.14, 269p., n.2, 2014 Recebido em: 07/03/2014 - Aprovado em: 26/04/2014
devised, some modern analytical tools will become useful in understanding the richness of its rhythmic intricacies and ambiguities. For that purpose this study will make use of a transcription elaborated by the author specifically for the present research, as well as some recent analytical systems, especially the unique view on metrical dissonances in Harald KREBS’s text (1999). Some of the historical documents and treatises, often contain- ing straightforward performing instructions and rules directed specifically to actual play- ers, largely amateurs, did not require a profound knowledge of the complications related to tactus; on the contrary, they were expected to be a solution for those who did not have the time (or the knowledge required) to spend in trying to figure them out. Nonetheless, although a thorough comprehension of meter was concealed from the performer, the com- poser was more likely to have been able to master it. Meter becomes of particular interest in regards to the way in which Uccellini notated this specific sonata, as well as the metri- cal dissonances resulting from both his compositional wit and the performer’s execution of the written music.
Approaching early-Baroque repertoire inevitably touches more general issues per- taining to its performance as well, such as the validity of modern editions and transcrip- tions and their function in contributing to historicity. Seventeenth-century music has re- cently received a boost when it comes to modern transcriptions from early editions, as more and more works, including those by minor composers, are becoming available in print as an alternative to facsimile editions. The only authoritative published transcription of the op. 4 presently available (UCCELLINI, 2000) comprises a clean and fresh rendition of all twelve sonatas in modern notation. But, in reality – and especially in the context of rhythm and meter –, what is a transcription for? Does it facilitate performance? Does it make the no- tation more accessible to the performer? Does it bring out rhythmic, metrical features and other musical qualities that are not clear from the first edition? Is it, therefore, ultimately significant for historicity? While these inquiries can be difficult to answer depending on the repertoire and work under study, there are cases that prove a challenge to editors. The Sonata ottava might well be one of them.
Justin LONDON (2013), in the New Grove article on rhythm, suggests that, as far as its history is concerned, it is not possible to come up with a single, unified theory of rhythm and meter by the beginning of the seventeenth-century. In this sense one could al- most say that there are as many interpretations of tactus and tempo as there are authors writing about them at the time. It was probably in this context that some theorists voiced their concern about issues to do with rhythm, especially the ones related to proportions and time signatures (in duple or triple meter). Michael Praetorius (2001), in 1618, talking about tactus, says:
When I examine the compositions of contemporary Italians, which within very few years have come to be set in an entirely new manner, I find many discrepancies and great variety in their use of signatures in both tactus aequalis and inaequalis. (p. 61)
He also shows his indignation at how carelessly contemporary composers them- selves regarded some of their own guidelines:
I see that most [writers] do not observe their own rules [concerning signatures] and use one indiscriminately in place of the other. Therefore it is my humble opinion that in order to keep from hindering students and singers with superfluous matters, all signatures shown above should be eliminated without hesitation (the more so since they prove unnecessary, useless, and indeed extremely involved), even though famous musicians have used them until now. Only the signature 3/1 or 3 should be used in tripla and 3/2 in sesquialtera. (p. 61)
In the specific case of time signature here, Praetorius has a very good reason to try to untangle the enormous amount of conflicting information accumulated throughout the Middle Ages and Renaissance and still very much present in the beginning of the seven- teenth century. But, on the other hand, so do all other authors, and yet nearly every single one of them comes up with a different, “better” solution, thus giving way to even more dis- crepancies. The problem is that concepts such as time signature and proportion not only indicated the tempo (or were supposed to do so), they actually influenced the way the notat- ed values were to be grouped and interpreted, becoming especially crucial in performance whenever bar lines were not notated.
It must have been in this context as well that performing musicians, in writing on instrument playing and other musical matters – and probably amateur musicians strug- gling to understand the complicated state rhythm and meter had reached –, started to de- velop essentially practical, rather simple rules intended for actual music making. One of the most well known of them concerns bowed instruments and right-hand technique. Although recent scholarship is not clear as to when exactly the “Rule of Down-Bow” was first coined as a term, different authors start giving distinctive indications that tackle a basic component of tactus: the difference between stress and release. Sylvestro GANASSI (2004, p. 26), in his Regola Rubertina from 1542, already hints on the relationship be- tween the down-bow and stress, suggesting that it should be preferably used on metrically strong notes. As BOYDEN (1990, p. 159) points out in his major historical work on the vio- lin, the physiological implications of drawing the bow are obvious enough in violin tech- nique. It is not only easier to draw the bow downwards because of the aid of gravity, but it technically requires a little more effort to draw it upwards – resulting in a weaker stroke
–, even though the baroque bow at this time would probably weigh as little as 60 grams. Hence, the sonorous product of a down-bow is usually a naturally more stressed stroke and, though the physics of drawing the bow varies from instrument to instrument (take the violin and the violoncello, for instance), the Rule of Down-Bow holds the same for all members of the violin family. In the viol family the opposite is logically applied, due to the different bow grip, with up-bow-strong and down-bow-weak strokes. George HOULE (1987, pp. 91-109), in his book on meter in the seventeenth and eighteenth centuries, pro- vides a comprehensive overview of how the Rule of Down-Bow is paralleled in wind and keyboard instruments, by means of specific tongue articulations and fingering patterns in function of the either metrically strong or weak notes. Girolamo DIRUTA (1983, p. 6), like many other authors, makes a clear distinction between note buone (good notes) and note cattive (bad notes), as well as how likewise “good” and “bad” fingers should be employed in playing them (DIRUTA, 1984, p. 56).
Modern bowing technique for the violin family, in its desperation to equalize and stabilize the sound and to make sure the bow stroke is steadily healthy through- out, choked some of the bow’s original speaking qualities. The outcome is, ideally, the achievement of a similar sound product between up and down bows, as well as an avoid- ance of effects that were fundamental to earlier technique and repertoire (such as messa
di voce, for instance) thus gradually eliminating the natural nuances, irregularities and variations of the bow stroke. In hearing a recording by a modern violinist, it is rather hard to tell nowadays in which direction he is drawing the bow. Bowings in solo and or- chestral repertoire are rather linked to physical commodity and comfort in playing spe- cific passages, instead of to any original major concern with metrical stress. Since bow strokes in both directions should possess the same strength, they can be organized as the player sees fit.
In some historical studies to do with the Rule of Down-Bow, researchers draw guidelines from what is probably the most well-known text on the subject: Georg MUFFAT’s (2001) preface to Florilegium secundum (1692), applying them to seventeenth- century violin music in general. There are, nevertheless, two main problems with that approach. First, that text has to do with French music by the end of the century. The Florilegium is a collection of works comprising dance music and, therefore, essential- ly differs from the compositions of the first half of the century in Venice. To be sure many of Uccellini’s compositions are still very much rooted in the stylus phantasticus established in Italy by Claudio Merulo and Girolamo Frescobaldi and, although a large amount of Italian musical production at this time is in fact dance music, only a small number was intended for actual dancing (BOYDEN, 1990, p. 150). Contrarily, French dance music is to a large extent governed by conventional metrical patterns pertaining to baroque dance itself, based on balance between specific steps and movements, thus shaping the structure of such pieces in a very idiosyncratic way. Italian instrumental music and especially works pertaining to the early Sonata genre, in turn, derive from the rhythmically freer toccatas and fantasias, being rather more flexible not only when it comes to any sort of metrical structure, but also to the actual notated surface rhythm. The second problematic point is that Muffat’s bowing propositions concern a repertoire that already counted on an established tradition of notated bar lines. Some of his in- structions require, if not a visual perception of bar lines, a relatively accurate notion of where they are placed. Uccellini’s op. 4, no. 8, because of its almost complete lack of notated bar lines in the separate parts, calls attention to a more contextual study of the Rule of Down-Bow in the first half of the century.
Riccardo ROGNONI (2002, p. 42) is the one to make a clear distinction between ti- rare (“T”, down-bow-strong) and pontare (“P”, up-bow-weak) bowings for the violin in 1592, but the instructions related to the “Rule” that approximate Uccellini’s music the most are found in the writings of his son Francesco Rognoni (1620), J. A. Herbst (1642) and Gasparo Zannetti (1645). The summary of the four most relevant guidelines from these authors, as collected by BOYDEN (1990, p. 159), is particularly thorough. The first general guideline is that, if there is a notated measure, a down-bow is used in the first note (Figure 1a). The sec- ond overwrites the first guideline and states that the first note of a measure (again, if there are notated bar lines) should start down-bow if the total number of notes in that bar is even; if it is odd it should start up-bow (Figure 1b, four notes in three beats, following a rest). It is of interest to note that this repertoire, unlike a great deal of dance music, does not pres- ent many upbeats containing an odd-numbered group of notes. The third guideline allows for alternated bowings in triple meter, meaning that in a group of four bars (here left to the reader’s imagination) with three notes each, bars one and three will start down-bow (Figure 1c). The fourth has to do with arrangements and bow corrections, implying two consecutive bow strokes in the same direction, either down or up, so as to accentuate the right notes in a given passage (Figure 1d).

Figure 1: Examples of bowings from Rognoni (1620), Herbst (1642) and Zannetti (1645), applied to passages from Uccellini, Sonata ottava, op. 4. The square-shaped symbol stands for down-bow as in modern usage, as well as the “V”- shaped symbol stands for up-bow.
The goal of these guidelines is that whenever possible a down-bow should be used on a metrically strong notated value. Of course this becomes particularly more complicated whenever there are few or no bars, as in Uccellini’s op. 4, no. 8, which will be analyzed in more detail below. More important than these four aspects of the Rule of Down-Bow, how- ever, is the fundamental instruction given by Francesco Rognoni (1970, Parte Seconda, p. 2): “the manner of handling the bow is that it is always drawn downwards in the beginning of the melody”1 (Figure 1e), or the prominent melodic figure (theme or larger motive), regard- less of its position in the bar or metrical unit. In fact, in this repertoire, the canto frequent- ly starts on an actual metrically strong point, but not in all cases. This rule will become invaluable in Uccellini’s Sonata ottava because its thematic material is very recurrent and the main motive appears time and again throughout the piece, giving a general indication of when the ‘canto’ starts and a down-bow should be used. However, this fundamental in- struction clashes with one of the options in the second guideline mentioned above, namely the one that states an up-bow should be used in the beginning of an odd-numbered group of notes preceding a metrically stronger one (such as a downbeat). Again we go back to the problem of missing notated bar lines. It is likely that musicians had to rely on a general feel- ing of metrical units, being able to perceive stronger and weaker starting points depending on where rests were placed and on the general flow of the music, although that becomes challenging when metrical dissonances and changes are involved. In this sense whenever there are no bar lines, a first-level default would be to draw the bow down in the beginning of melodic figures; overwritten by the second-level default up-bow – used whenever one is more sure of the metrically weak character of the first note and/or aware of an immediately subsequent strong metrical point.
This contrapuntally interesting and unique specimen from the repertoire is an as- tounding example of rhythmic ambiguity, metrical changes/reinterpretations and metrical dissonances at multiple levels. It certainly goes beyond the concept of bar line, to be fully developed and established about half a century down the road from when it was composed. The almost complete absence of bar lines in the first edition requires the application of the Rule of Down-Bow, and especially the fundamental instruction given by Rognoni regard- ing melodic groups; that of a down-bow in the beginning of a theme. Employing the Rule of Down-Bow will not only help the music to keep flowing and the player to keep track of his part in the metrical chaos that it eventually becomes, but it will also be the very factor em- phasizing these metrical conflicts by creating non-coinciding local accents. The continuo part has more notated bar lines (15 in total), but not consistently or periodically distributed throughout the staves.
The form of the Sonata ottava is a simple, tripartite A-B-A’ layout (Figure 2), com- prising an imperfect-perfect-imperfect prolatio setup in the time signature that helps to di- vide the piece into three visually distinct blocks. The first question is how long the measure unit is in A. Although the semicircular symbol “C” in the key signature represents 4/4 in modern notation, some treatises allow for other interpretations: 2/2, 4/2, and so forth. In this sense the tactus could be as long as a breve. Nevertheless, Uccellini provides a bar line in the first staff of the violin part (Figure 3). Since the number of crotchets preceding this bar line (indicated by the arrow) is 28, the number of bars preceding it should be either 7 semi- breve-long, 14 minim-long, or 28 crotchet-long bars (!). As the last two options are rather ab- surd, the best option is 7 semibreve-long bars (“C” = 4/4). As shown in Figure 3, breve-long measures would ignore the notated bar line provided by Uccellini in the violin part, because measure groupings that are longer than a semibreve would exceed it. Even though it may be hard for the violinist to notice that, Uccellini placed that specific bar line there for a reason, which is probably to inform the performer that the meter is indeed 4/4 and that at that point he is crossing a metrical boundary of some sort. The bar unit in B is more straightforward, being as long as a dotted breve. In modern notation the 3/1 provided in the score (accompa- nying the dotted semicircle in the time signature) is equivalent to a 3/2 signature. Again, the quantitative, notational length of the tactus still varies from author to author at this time.

Figure 2: Form of Uccellini’s Sonata ottava, op. 4, no. 8.

Figure 3: One of the few notated bar lines in the first staff of the violin part. Uccellini, Sonata ottava, op. 4. Vertical lines stand for hypothetical metrically strong points at the minim, semibreve and breve levels.
The end of section A elides with the beginning of B in a perfect authentic cadential point at the fifth D minor. This turning point between A and B is an example of one of the main struggles for practical musicians at the time: figuring out the metrical proportion be- tween two sections comprising different meters or prolatio. The aforementioned discrepan- cies in defining proportions from author to author still allow for some flexibility in choos- ing an adequate tempo at the point of change. The favourite candidate would probably be the equivalence between a half note in the duple meter and a dotted half note in the triple meter. Consequently, in the beginning of the B section, a whole bar in the triple signature would correspond to half a bar in the original duple signature. In other words, the com- plete cycle of arsis and thesis accomplished in one whole bar in A corresponds to two bars in the new tempus imperfectum–prolatio maior in B (duple tactus, triple subdivision – one
bar being metrically strong and one weak), indicated in the time signature (a dotted semi- circle in the original edition, reproduced in Figure 2). In this sense all three sections are in duple meter at a tactus level, B being in triple meter at the “bar” level and both A and A’ being duple. Thus, the 48 bars of B can be regarded as 24 in relation to A and A’, making it the shortest section, resulting in a rough balance between B + A’ and A.
One last consideration on bar lines has to do with the B section. In Figure 4a Uccellini curiously uses a tie over a minim and a crotchet, instead of the dotted minim used in all ensuing motivic groups. He certainly wanted to inform the violinist that he was cross- ing an omitted bar line there. Interestingly in Figure 4b, where another omitted bar line is crossed, he uses a dotted minim in place of the tied notes in 4a. This is probably due to the fact that 4b is very close to one of his rare notated bar lines, meaning the performer was less likely to have trouble with the meter. All in all, despite Uccellini’s endeavours to indicate omitted bar lines, the Rule of Down-Bow remains the preferred guidance for the performer.

Figure 4: Notation related to omitted bar lines. Uccellini, Sonata ottava, op. 4.
Each of the sections in the piece (A-B-A’) comprises a wandering away from and back to metrical consonance (C in Figure 2). It is in these three dissonant cores (D) that met- rical conflict arises, apart from which the music is quite stable. Given the fact that poly- phonic music is rather likely to be metrically dissonant to some extent, due to imitative contrapuntal activity, conflicting regions chosen for this analysis include only tighter dis- sonances that call for attention, where at least one part is dislocated in relation to the bar line in the transcription (larger motivic materials that are out-of-phase by a whole bar or more are not, for the present purpose, analyzed as metrical dissonances due to their looser nature). As for the relationship between the dissonant portions from each sections, they go along with the piece’s A-B-A’ formal structure. While the metrically dissonant areas in the A and A’ sections are analogous, the one in the contrasting middle is clearly more energetic, suggesting an intensification of the dissonance quality from A into the B section, and a re- lease towards the recapitulatory end – A’. In spite of the impossibility to draw parallels to a “tonal realm”, given the modality of the repertoire, the middle section opens at the fifth D minor creating a harmonic contrast, while A and A’ are mostly centered around a G minor aura2. The instability of the Dorian mode (also evidenced by the B-flat in the key signature) is felt throughout, especially when it comes to the ambiguity between E-flats and E-naturals.
Attempting to identify larger hypermetrical units proves to be quite problematic in this piece, but the opening twelve measures, paralleled in the beginning of section A’ (mm. 94-99) do give a general sense of an alternate strong-weak structuring (at every two bars). The same holds true for the beginning of the B section, probably one of the only mo- ments of the piece where a stable, quasi-dance-like character is felt. Of interest in this so- nata, however, are the metrical dissonances in each of the sections. Although the following analyses of these dissonances rely chiefly on KREBS’s (1999, pp. 22-61) system3, their na-
ture in this repertoire is largely distinct from the post-Classical works he deals with in his book. The achievement and intensification of the actual metrical dissonance are much sim- pler in construction and generally freer, also due to their independence from tonality and other musical factors pertaining to later composition techniques. Extensively, dissonances occur in this piece depending on the relationship between what is hereafter called motivic cells. In this sonata metrical dissonances are ultimately created, intensified and resolved by means of (1) mutation within a cell or (2) overlapping of two adjacent cells. In the case of mutation, Uccellini altered specific cells by means of shortening (SC, Figure 5) or extend- ing them (EC, Figure 6). Both a cell that is shortened one beat, and a cell whose last beat overlaps with the first in the next cell (OC, Figure 7), will cause the ensuing motivic cell to come in one beat sooner. A cell that is extended one beat, in turn, will logically cause the subsequent cell to come in one beat later. It is generally by employing these three devices (each time resulting in a displacement equivalent to one beat) that Uccellini either created, intensified or resolved these metrical dissonances.

Figure 5: Example of a shortened cell (SC). In this piece a shortening occurs by means of eliminating the last beat of a motivic cell immediately followed by the next. Like in the OC case in Figure 7, the result is the subtraction of an entire beat4.

Figure 6: Example of an extended cell (EC). In this sonata the extension can occur in either the first or last beat of the motivic cell, indicated by the arrows.
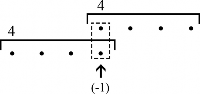
Figure 7: Example of overlapping cells (OC). The arrow indicates the point where cells overlap in this piece, resulting in the subtraction of one beat.
Because the continuo line in this sonata is basically the same as the Basso and both complement each other, they will generally be considered to be essentially one part. The slight variations between them are likely to be related to the instrument devised to play- ing them: the bottom part is idiomatically a continuo line with a few figurations, and the middle part is intended for a solo instrument, probably a dulcian. Therefore, with a few ex- ceptional instances in which the middle part is elaborated by means of diminutions on the bass line (not contrapuntally significant to be a third part), this is essentially a two-part so- nata for violin and continuo with a supporting bass instrument.
A section. The first section is characterized by KREBS’s (1999, pp. 30-38) displace- ment dissonances only, and its metrically dissonant core takes place in bars 13-23 (Figure 8). The first beat of measure 13, in the violin part, holds the ending note of the previous melodic line, thus already creating the first set of displacements against the bass, due to a succession of bar-long motivic cells starting immediately on the second beat. These cells
derive from the beginning of the opening theme (more precisely – the entire first bar) and will become the most recurrent rhetorical unit.

Figure 8: Sonata ottava, mm. 13-24. Author’s transcription5 based on the original edition (UCCELLINI, 1984). Metrical dissonance in the A section.
According to Rognoni’s fundamental rule discussed above, this motive (canto) should begin with a down-bow. The bass carries the same motivic cells in succession, only they are in-phase with the grid. The resulting displacement dissonance – D4+16 in KREBS’s terms (1999) – is carried out for three bars and the first altered motivic cell (EC) is intro- duced in the bass (m. 16). The extra beat (+1) in this instance is found on the downbeat of that bar. The result is an immediate synchronization of the two parts (mm. 17-21). In spite of being synchronized with one another, both parts generate a displacement dissonance with the metrical grid (D4+1). Now, as far as bowings are concerned in this passage, one of the two early-seventeenth-century available bow-grip techniques used in Italy at the time placed the thumb on the bow-hair, instead of on the stick, making it more difficult for the violinist to retake the bow as freely in playing two consecutive down-bows. Therefore, the bow must rest on the string almost constantly, requiring a brief pause in between two bow- ings in the same direction, so as to actually detach the two. This may create a slightly lon- ger break between those two notes than in drawing the bow alternately down and up. In playing the scalar motivic cells in bars 19-21 (first introduced by the bass by means of its EC in bar 16), for instance, every one of them would be to some degree detached from the following as a melodic unit, due to the repeated bowings in the same direction, consequent- ly intensifying the thematic cells in the bass with which they are in-phase. When the same scalar motivic cells happen in the continuo part, in addition to similar rules to do with fin- gering, the keyboardist is likely to slightly detach one melodic unit from the other due to the downward skips between them. The thumb is not as frequently employed in some six- teenth- and seventeenth-century instructions as it is in modern keyboard technique, mean-
ing the player had to physically move the entire hand in order to cover the gap between the two notes on the keyboard. DIRUTA (1984, pp. 63-65) talks about the “good” and “bad” leaps in both hands, and addresses some difficulties to do with fingering (“good” and “bad” fingers), providing exercises for the left hand that are in fact very similar to this passage.
The downbeat of bar 22 comprises an overlap in the violin part, between the last beat of the motivic cell in bar 21 and the first beat of the new cell in bar 22, bringing back the main thematic element. The violin part is finally in-phase with the grid again, but the bass remains out-of-phase with it for a little longer. Since the violin part is now lingering one beat behind in relation to the bass, the metrical dissonance comes back in the form of D4-1. A scheme of the dissonance trajectory is provided in Figure 9.
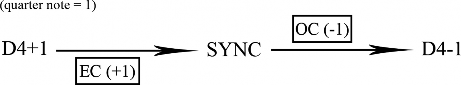
Figure 9: A section. Scheme of metrical dissonances changes by means of extended and overlapping cells, mm. 13-23. Rectangles above the arrow indicate occurrence in the violin part, and below in the bass parts.
The point of synchronization (“SYNC” in Figure 9, mm. 17-21) is hereafter referred to as such, instead of consonance (although the dissonance is in fact temporarily resolved between the parts), because both parts are still out-of-phase in relation to the grid. It is true that in the original edition there are no bar lines, but Uccellini was certainly aware of this metrical shift. In this sense, bars 13-16 work as a metrical transition to the upbeat-strong meter (mm. 17-21), gradually setting both parts to be out-of-phase with any metrical sense the performer might still have at this point. Hence, he creates an ambiguity between the original downbeat and the (now strong) second beat. What is important for the violinist in keeping track of the beat rate is to rely on the Rule of Down-Bow to play the succession of motivic cells, instead of trying to keep track of the original meter.
A’ section. The architecture of the final section is in many ways analogous to the first, though shortened in length. Its dissonant core, despite being constituted of the same thematic material only, is slightly larger in comparison to the A section and heightened in activity (mm. 100-112, in Figure 10). It starts identically to the corresponding passage in A, but is promptly disturbed by an EC. It is difficult to tell how this cell is employed, since this is a spot in which what happens in the continuo differs considerably from the soloing middle part (mm. 102-103). An EC seems to occur in the bass in bar 103 (similarly to bar 16 in the first section), where an extra beat is added to the beginning of the cell. What happens in the middle part, however, suggests that it is bar 102, instead, the one to be extended (+1) in the last beat of the cell. The latter interpretation is supported by an immediate identical occurrence in the violin, another EC. In any case, since all parts are extended one beat the D4+1 displacement dissonance between the parts remains the same. Now the scalar motiv- ic cell is used in both parts in counterpoint to one another, which does not happen at all in the A section – an evidence of heightening activity in A’.
The overlapping cells in measures 106-107 drag the bass part one beat behind, al- lowing for a looser D4+2 dissonance. Though quite simple musically and perhaps dull when it comes to the counterpoint, the flexibility of these motivic cells (liable to be super- posed in a variety of ways) advocates for Uccellini’s careful composition. The ensuing com- bination of two adjacent OCs in the upper part (m. 109) and an EC in both bass parts (mm. 109-110 – identical to mm. 102-103) resolves the D4+2 dissonance at once into a synchroni-
zation – again out of-phase with the grid and at last moving into different material, from bar 113 (an imitative descending melodic pattern between the parts), that quickly brings the so- nata to an end. This heightened dissonance trajectory is portrayed in the chart in Figure 11.

Figure 10: Sonata ottava, mm. 97-114. Metrical dissonance in the A’ section.

Figure 11: A’ section. Scheme of metrical dissonances changes by means of extended and overlapping cells, mm. 100-113.
B Section. The dissonant core of the contrasting middle constitutes what is by far the most interesting and metrically intricate spot in the whole work (mm. 67-78, Figure 12). Uccellini seems to utterly ignore the bar line here, or any feeling of meter, providing a cha-
otic chain of motivic cells that convey a duple quality, rather than the triple organization suggested by the time signature. The violin comes in abruptly in measure 68 after a short pause, imitating the opening motive from the duple prolatio carried by the bass. This is the first time the main theme is heard in a D4+2 dissonant displacement against itself. Because this motivic cell is used in the triple prolatio, this metrical dissonance becomes especially noteworthy. The only occurrence of a shortened motivic cell (SC) is found in this core, and its employment in the violin part delays the upper part creating a tighter D4+1 (mm. 71-72). The beginning of this passage in the basses (m. 67) offers this same shortened motivic cell. The end, bringing about a not less metrically unstable hemiola in bars 76-77 (by definition a G3/2 grouping dissonance against the grid7), achieves a general synchronization, due to the overlapping cells in the violin part (mm. 76-77). The music cadences in the final of the mode, being followed by metrical consonance and a partially homophonic structure, thus dissipating the energy of the dissonance.

Figure 12: Sonata ottava, mm. 67-78. Metrical dissonance in the B section.
The following chart depicts the metrical dissonance trajectory in B (Figure 11). Apart from the concluding hemiola, the basses have six straightforward, duple meter cells with no overlaps or mutations, being in a constant grouping dissonance G4/3 (KREBS, 1999, pp. 30-38) against the bar line – the intensification and resolution of the dissonance are left to the upper part (Figure 13). The asterisks in Figure 10 indicate the points where the cells are in-phase with the visual grid, both in the bass and in the violin.
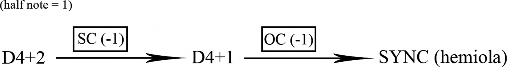
Figure 13: B section. Scheme of metrical dissonance changes by means of shortened and overlapping cells, mm. 68-77.
Perhaps needless to say, this whole sonata transcends the bar line to a great extent. The Rule of Down-Bow, as a historical tool, is in itself enough guidance for the violinist throughout the piece, since the composer intended it to be metrically ambiguous and most probably omitted the bar line indications so as to allow for a freer perception and interpre- tation in which this dubiousness in meter could be both seen in the notation and heard in sound. Such liberty from the notated grid would only be substantially felt again years later in music history, since the establishment of the bar line, though a major accomplishment in music theory as an organizing factor, is in many ways psychologically restricting in com- position and performance.
A second rather obvious concluding outcome is that a modern edition intended for performance, at least in the case of this sonata, does not prove to be at all useful. The ad- dition of bar lines is not only unnecessary, but also quite disturbing in the process of both understanding and performing meter/rhythm, rather clouding the original music instead of clarifying it. It also does not bring out any musical features by means of the modernized vi- sual representation, since the first edition of 1645 is already very clear (although it is true that some effort is required from a modern performer to get used to some of the notational symbols and style). The positive aspect in transcribing music from historically early edi- tions is the correction of eventual obvious mistakes, but in this case that does not occur. From the stand point of analysis only, however, snapping this music to a grid with either bar lines or periodic indications of some sort, helps defining and visually observing how these motives and figures trick any sense of metrical continuity indicated in the time sig- nature. I particularly believe that what is ultimately at stake here is the visual aspect of bar lines – while they may complicate performance, especially at first sight, they become ben- eficial for analytical purposes as an aid in identifying metrical dissonance.
1 La maniera di portar l’arco e questa ache sempre si tira l’arco in giù nel principiar del canto. In this passage Fran- cesco Rognoni is talking about the viola da gamba, but, in any case, both he and Riccardo Rognoni agree that the bow direction is the same for the da gamba and da braccio families (which is the case of the violin).
2 Speaking strictly of tonality here is not only out of context, but will also prove unnecessary in analyzing this repertoire.
3 Although Harald KREBS’s (1999) procedures for analyzing metrical dissonance are quite straightforward and rather intuitive, reference to his full text is highly recommended for clarifications on nomenclature and usage within this article.
4 In examples 5 through 7 the dots represent the number of beats in the cell. The arrows indicate potential points of shortening or extension equivalent to one beat (+1 or -1).
5 The transcription used in this research paper was elaborated by the author and based on the original 1645 edi- tion (UCCELLINI, 1984). The bar line divisions used in this transcription were added for analytical purposes and also appear in Alessandro Bares’s modern edition (UCCELLINI, 2000).
6 KREBS (1999, pp. 22-61) suggests the nomenclature Da+b for a displacement dissonance between two metrical layers of equal metrical cycles, where a stands for the number of beats in a given metrical layer, and b for the number of beats in the displacement. Thus, D4+1 indicates that two superposed metrical layers, both compris- ing 4-beat-long cells, are displaced by one beat. Throughout this article displacements dissonances generally have the bass as reference, since they always begin in-phase with the grid in all three dissonant sections of the piece. Therefore, the first number (a) will always refer to the bass part, while the second (b) will refer to the soprano part.
7 KREBS (1999, pp. 22-61) suggests the nomenclature Ga/b for grouping dissonances between two metrical layers of different metrical cycles, where a stands for the number of beats in one of the layers and b for the number of beats in the other.
BOYDEN, David. The History of Violin Playing from its Origins to 1761: and its Relationship to the Violin and Violin Music. New York: Oxford University Press, 1990.
DIRUTA, Girolamo. Il Transilvano: (1593, 1609). Buren: F. Knuf, 1983.
DIRUTA, Girolamo. Il Transilvano. Murray C. Bradshaw and Edward J. Soehnlen, ed. Henryville: Institute of Medieval Music, 1984.
GANASSI, Sylvestro. Regola Rubetina (1542) e Lettione Seconda (1543). Christine Vossart, ed. Sprimont: Pierra Madarga, 2004.
HOULE, George. Meterin Music, 1600-1800: Performance, Perception, and Notation. Bloomington: University of Indiana Press, 1987.
KREBS, Harald. Fantasy Pieces: Metrical Dissonance in the Music of Schumann. New York: Oxford University Press, 1999.
LONDON, Justin. “Rhythm, §II: Historical studies of rhythm”. Grove Music Online. Available at: http://www.oxfordmusiconline.com.myaccess.library.utoronto.ca/subscriber/article/grove/ music/45963pg2#S45963.2. Accessed November 10, 2013.
MUFFAT, G.; WILSON, D. K. George Muffat on Performance Practice: The Texts from Florilegium Primum, Florilegium Secundum, and Auserlesene Instrumentalmusik. Bloomington: Indiana University Press, 2001.
PRAETORIUS, Michael, Hans Lampl, and Margaret Boudreaux. The Syntagma Musicum of Michael Praetorius, Volume Three: An Annotated Translation. [S.l.]: American Choral Directors Association, 2001.
ROGNONI TAEGGIO, Francesco. Selva de varii passaggi. Facsimile edition. Bologna: Forni, 1970.
ROGNONI, Richardo. Passaggi per potersi essercitare nel diminuire. Facsimile edition. Bologna:
Forni Editore, 2002.
UCCELLINI, Marco. Sonate, correnti, et arie da farsi con diversi stromenti si da camera, come de la chiesa, à uno à due, à trè. Opera Quarta. Facsimile edition. Florence: Archivum Musicum, 1984.
UCCELLINI, Marco. Sonate, correnti, et arie da camera e da chiesa, a uno, due e tre strumenti: op. 4, Venezia, 1645. Modern edition by Alessandro Bares. Albese con Cassano, Italia: Musedita, 2000.
![]()
Eduardo Solá - Bacharel em violino barroco e performance histórica (BMus) pelo Koninklijk Conservatorium Den Haag (Conservatório Real de Haia), na Holanda, e em violino moderno (BMus) pela Escola de Música e Belas Artes do Paraná. É mestrando em musicologia (MA) pela University of Toronto, Canadá, onde também trabalha como professor assistente em pesquisa histórica e música do século XX para o teatro. Em 2014, lançou no Brasil o seu primeiro livro “O Menino e o Som”, pela editora Metanoia. Atua como violinista internacionalmente tanto como solista como músico de câmara e em formações orquestrais.
![]()