

Revista Música Hodie, Goiânia - V.14, 238p., n.1, 2014
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
Zoltan Paulinyi (Universidade de Évora, Portugal)
paulinyi@yahoo.com/zoltan.paulini@gmail.com
Resumo: Série oni-intervalar (do inglês “all-interval”) é aquela que possui todos os intervalos de 1 a n semitons, onde n é o número de notas da série. Tais séries são particularmente úteis à composição quando possuem propriedades agregadas, como a presença ou exclusão de tricordes ou de outros subconjuntos harmônicos. Oni-intervalaridade foi assunto prematuramente estagnado devido às limitações computacionais das décadas de 1960-1970, que estimulou indevida associação da oni-intervalaridade ao conceito de classes de alturas, prejudicando a análise de contornos melódicos. Este artigo propõe um aperfeiçoamento inicial do algoritmo gerador de séries oni-intervalares e mostra três exemplos musicais de obras brasileiras recentemente estreadas na Europa.
Notable All-interval Series
Introdução histórica
O desenvolvimento teórico e composicional do século XX proporcionou a for- mulação do conceito de “classe de altura” (“pitch class”) por Milton Babbitt na década de
1950 (MORRIS, 1995, p. 207), que estende formalmente a equivalência de oitavas para além da região de vizinhança:1 uma classe de alturas representa uma determinada altu- ra em qualquer oitava. Classes de altura são numeradas a partir do Dó = 0 até Si = 11, atualmente.2
Esse conceito é comumente empregado em análise de música dodecafônica porque o dodecafonismo registra simplesmente o total cromático pelo nome ou símbolo da nota. Contudo, dentro do conjunto de obras que originaram o atonalismo e dodecafonismo, é necessário proceder com cautela a respeito da equivalência de oitavas. No início da Suíte Lírica de Alban Berg (1927), compassos 2-4 do exemplo 1, o primeiro violino apresenta uma série oni-intervalar,3 a qual possui todos os intervalos de 1 a n semitons, sendo n o número de notas da série. Tal série oni-intervalar percorre quase duas oitavas heptatônicas totali- zando 21 semitons: {5, 4, 0, 9, 7, 2, 8, 1, 3, 6, 10, 11}. Evidenciada no exemplo 2, a série apre- senta propriedades notáveis: utiliza, sem repetição, 12 classes de altura e 12 intervalos com sentidos alternados. Apesar do uso da totalidade de classes de altura, a exigência do contor- no melódico anguloso não permite assumir que as oitavas sejam claramente equivalentes.4
De fato, a teoria de contornos dificilmente admite uso de equivalência de oitavas ou de clas- ses de alturas, mas apenas de alturas reais, como se verá claramente no contraexemplo da
“série de diamante” no fim desta seção.
Revista Música Hodie, Goiânia - V.14, 238p., n.1, 2014
![]()
171
Recebido em: 06/09/2013 - Aprovado em: 15/03/2014
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182

Exemplo 1: início da Suíte Lírica de Alban Berg (1927), c.1-6, no qual a série oni-intervalar que se encontra no primeiro violino (c.2-4) abrange 21 semitons, extensão maior do que uma oitava heptatônica.

Exemplo 2: série oni-intervalar do exemplo anterior, contida no início da Suíte Lírica de Alban Berg. Sequência de intervalos (números indicam semitons): < -1, +8, -3, +10, -5, +6, -7, +2, -9, +4, -11 >.
Na década de 1960, o limite do poder computacional possivelmente impôs maio- res restrições ao desenvolvimento de algoritmos oni-intervalares, de modo que Bauer- Mengelberg e Ferentz (1965, p. 93) decidiram reescrever esta série para registrar somente intervalos ascendentes (Exemplo 3). Baseado nisso, Morris e Starr (1974, p. 367) escre- veram e implementaram um algoritmo em Fortran para gerar séries dodecafônicas oni-
-intervalares. Justificou-se este “endireitamento” invocando o princípio da equivalência de oitavas:
Séries dodecafônicas que diferem entre si somente por haver notas individuais trans- postas por uma ou mais oitavas em qualquer direção são, obviamente, consideradas como idênticas; isto quer dizer que uma série dodecafônica será a mesma indepen- dentemente da oitava em que uma nota aparecer, desde que a ordem das notas não seja alterada. Esta convenção permite-o “endireitar” a série de Berg da seguinte ma- neira: (BAUER-MENGELBERG e FERENTZ, 1965, p. 93)
![]()
172
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182

Exemplo 3: adaptação da série anterior alterando-se o registro das notas sob invocação do princípio da equivalência de oitavas para obter série apenas com intervalos ascendentes. Sequência de intervalos (números indicam semitons): < +11, +8, +9, +10, +7, +6, +5, +2, +3, +4, +1 >.
Sob a justificativa do “endireitamento”, curiosamente, esta série deformada (Exemplo 3) mantém a característica oni-intervalar ao se considerar apenas intervalos as- cendentes; ou seja, entre Fá e Mi (entre as classes de altura 5 e 4), considera-se um interva- lo de 11 semitons ascendentes no lugar de 1 semitom descendente. Comparando-se os dois exemplos anteriores, há profundas alterações tanto no contorno melódico quanto no orde- namento intervalar, fato que dificilmente sustenta um aprofundamento analítico baseado nessa justificativa. Dado isso, todo o restante deste artigo almeja substituir a hipótese de “endireitamento” de séries de Bauer-Mengelberg e Ferentz (1965, p. 93) pelo desenvolvimen- to de algoritmos que respeitam o contorno melódico serial.
Um simples contraexemplo invalida a premissa de equivalência de oitavas para o “endireitamento” de intervalos: a “série de diamante” {4, 7, 8, 1, 11, 0, 9, 3, 5, 10, 2, 6} inva- lida o axioma da equivalência de oitavas no “endireitamento” de séries. Nesta série, as três últimas alturas referem-se a um Lá#, Ré e Fá#. Se Ré e Fá# estivessem na oitava acima, for- mariam duas terças maiores seguidas. Contudo, na série de diamante, o penúltimo interva- lo é uma sexta menor que completa a totalidade de intervalos dentro da série. No algoritmo Fortran baseado na equivalência de oitavas, esta série estaria eliminada. Portanto, o endi- reitamento da série conduz à eliminação indevida de séries oni-intervalares no algoritmo baseado na retificação melódica em intervalos ascendentes. Ademais, este contraexemplo prova que a teoria de contornos não admite necessariamente a premissa da equivalência de oitavas, porque a mudança de alturas reais pode alterar o contorno melódico. Contornos me- lódicos e classes de alturas são conceitos que não se combinam facilmente.
Esta introdução histórica revela uma necessidade de se retomar a oni-intervalarida- de com algoritmos aperfeiçoados, expandindo e atualizando o assunto para além do domí- nio dodecafônico. Justifica-se a importância da oni-intervalaridade por explorar proprieda- des intervalares notáveis na composição musical, perceptíveis pelo intérprete e pelo ouvinte sem auxílio tecnológico.
1. Objetivo e metodologia
Para revisar e atualizar a investigação sobre oni-intervalaridade, este texto propõe um novo algoritmo para geração de séries oni-intervalares. Tal algoritmo deverá ser flexível com relação ao número de notas da série, bem como prever a incorporação de propriedades intervalares adicionais, principalmente tricordes, os quais são úteis às várias formas de es- truturação composicional.
Para não exceder o espaço deste artigo, serão apresentados alguns resultados notáveis do algoritmo proposto em vez da listagem do programa escrito em Linguagem C++, que pos- sui 350 linhas e que necessita de análise específica em outro texto mais extenso. Este novo algoritmo utiliza o total cromático respeitando o contorno melódico restrito a uma oitava ape-![]()
173
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
nas. Este procedimento não adota, por conseguinte, o conceito de classe de alturas nem de equivalência de oitavas, deixando ao compositor a criação de métodos para emprego de séries.
O artigo conclui-se apresentando exemplos musicais de obras brasileiras estreadas
no exterior, as quais ilustram variadas formas de utilização das propriedades oni-interva- lares citadas neste artigo. O esforço em incluir exemplos musicais torna o assunto visível a compositores, analistas e músicos em geral, evitando-se restringir o tema a especialistas te- óricos. Em que pese ser algo técnico este método para elaboração de séries oni-intervalares, suas propriedades são notáveis para o intérprete e audíveis pelo ouvinte, sem necessidade de intervenção computacional para tal percepção.
2. Séries oni-intervalares notáveis.
Amadurecendo as intenções originais de Bauer-Mengelberg e Ferentz (1965) e o al- goritmo de Morris e Starr (1974) escrito em Fortran, este estudo propõe novo algoritmo gera- dor de séries oni-intervalares, mais flexível com relação ao número de notas e com possibi- lidades de incorporar propriedades intervalares adicionais (Exemplo 4).
1. Estabelece a primeira nota da série.
2. É necessário completar a série? Sim: adiciona nota nova. Não: troca a altura da nota atual.
3. Atingiu a altura máxima? Se sim: volta ao elemento anterior da série e ao item 2.
4. A altura é repetida? Se sim: volta ao item 2.
5. Outras verificações: tricorde indesejável? repetido? Se sim: volta ao item 2.
6. Completou a série? Se não: volta ao item 2. Se sim: imprime o resultado.
7. Retrocede uma nota e volta ao item 2 até varrer todas as 12 alturas nominais em todos os elementos da série.

Exemplo 4: nova proposta de algoritmo gerador de séries oni-intervalares, a qual respeita contornos melódicos e incorpora verificações adicionais de propriedades notáveis, como presença/exclusão de tricordes.
Este algoritmo possui algumas características importantes:
a) utiliza alturas reais, não propriamente classes de alturas. Isso não impede o compositor de substituir posteriormente as alturas pela representatividade de suas classes.
b) não se limita a 12 notas.
c) permite incorporação de propriedades adicionais. No item 5, por exemplo, cons- ta a verificação de tricordes que o programador (compositor) deseja incluir ou excluir. Tais tricordes são aqueles listados na Tabela de Allen Forte (1973, p. 179).
Esse algoritmo foi implementado em Linguagem C++ para acelerar a geração de sé- ries oni-intervalares. O código não é listado nem analisado neste artigo por reservar espaço à divulgação e análise de resultados com seus exemplos musicais.
O item 5 deste algoritmo, na implementação do autor, além de verificar a presença ou ausência de tricordes a critério do programador, permite realizar verificações de borda, i.e., relações de clausura em ambas as extremidades da série. Há 3 níveis de verificações para tricordes:
• nível 0 = sem verificação alguma;
• nível 1 = verificam-se as duas últimas notas da série com a primeira;
• nível 2 = verifica-se a última nota da série com as duas primeiras.
A “série de diamante” {4, 7, 8, 1, 11, 0, 9, 3, 5, 10, 2, 6}, por exemplo, possui os se- guintes tricordes listados no exemplo 5.![]()
174
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
Subconjuntos de 3 alturas | Classificação Forte |
{4, 7, 8} | 3-3 |
{7, 8, 1} | 3-5 |
{8, 1, 11} | 3-7 |
{1, 11, 0} | 3-1 |
{11, 0, 9} | 3-2 |
{0, 9, 3} | 3-10 |
{9, 3, 5} | 3-8 |
{3, 5, 10} | 3-9 |
{5, 10, 2} | 3-11 |
{10, 2, 6} | 3-12 |
{2, 6, (4)} (nível 1 de clausura) | 3-6 |
Exemplo 5: categorias de tricordes sequencialmente presentes na “série de diamante” {4, 7, 8, 1, 11, 0, 9, 3,
5, 10, 2, 6}, que se notabiliza pela não repetição de tricordes até o primeiro nível de clausura.
Como consta no Exemplo 5, a série de diamante destaca-se por não repetir tricordes até o primeiro nível de clausura.5
Com este algoritmo, um compositor pode gerar ou selecionar séries com diversas propriedades intervalares úteis à sua criação. Por exemplo, é possível gerar séries dodeca- fônicas sem tricordes tonais, especificamente sem acordes perfeitos maiores e menores, au- mentados ou diminutos. O Exemplo 6 lista séries que possuem essa propriedade ao nível
2 de verificação de borda. Tais séries, cognominadas “de prata”, encontram-se listadas em pentagramas para reforçar o fato de que este artigo atém-se às alturas em vez de classes de alturas.
![]()
175
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
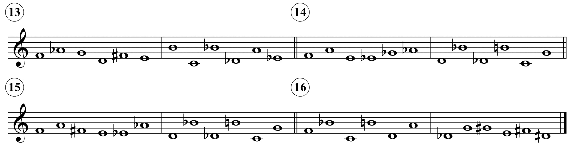
Exemplo 6: séries dodecafônicas oni-intervalares “de prata”, com todos os tricordes exceto acordes diminutos, perfeitos e aumentados, sob verificação de borda em nível 2.
Estas séries “de prata” são aproveitadas para estruturar a ópera “Biblioteca” com música e argumento de Paulinyi e libreto de Macedo (2011). A ópera possui dois persona- gens anônimos, um escritor e uma advogada, que vão à biblioteca com finalidades diferen- tes: o primeiro para buscar inspiração ao seu trabalho na elaboração de um livro sobre o diálogo, o outro para estudar aspirando ao cargo de juiz. No silêncio do local, a troca de olhares os motiva a imaginar julgamentos um sobre o outro, despertando paixão e raiva. O argumento, fundamentalmente filosófico, reúne duas questões: a limitação da eficácia do diálogo – agravado pela ação transcorrer em local de silêncio imposto – e o acúmulo de jul- gamentos, resultado da soberba humana em pretender assumir um atributo divino que não lhe é próprio. Malgrado não ser ópera dodecafônica, o dueto de amor da cena 6 é bastante ortodoxo na adoção dos preceitos dodecafônicos. O anacronismo da dodecafonia em obra contemporânea visa amplificar a contradição entre as idealizações criadas pelas persona- gens e a realidade apresentada pelo enredo. O exemplo 7 apresenta o uso pianístico da série n.7 do exemplo anterior, sob as formas retrograda e original.
Exemplo 7: parte de piano da ópera “Biblioteca” (PAULINYI e MACEDO, 2011), no qual a ponte à cena 6, c.531-
535, apresenta a série #7 retrogradada (do exemplo 6), seguida de sua versão original.
O algoritmo, apresentado acima, funciona para geração de séries com diversos nú- meros de elementos. Tomando como exemplo séries de 8 notas sem tricorde perfeito maior ou menor, aumentado nem diminuto (restrições semelhantes às séries anteriores), evitando tricordes repetidos e fazendo todas as verificações de borda (nível 2), obtém-se as 8 séries listadas no exemplo 8. Deste total, metade é inversão melódica: as quatro últimas séries cor- respondem às quatro primeiras invertidas. Considerando apenas as primeiras 4 séries, ob- serva-se que as duas primeiras são retrogradações das duas seguintes (em itálico), fato que se repete na segunda metade do exemplo 8, séries #5 a #8. Como são 9 tricordes para 8 no- tas, ausenta-se o tricorde semitonal 3-1 de todas essas séries.![]()
176
![]()

PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
#1: {1, 7, 0, 5, 4, 2, 6, 3}
Tricordes: 3-5, 3-9, 3-4, 3-2, 3-6, 3-3, 3-7, 3-8
#2: {2, 6, 3, 1, 7, 0, 5, 4}
Tricordes: 3-3, 3-7, 3-8, 3-5, 3-9, 3-4, 3-2, 3-6
#3: {3, 2, 7, 0, 6, 4, 1, 5}
Tricordes: 3-4, 3-9, 3-5, 3-8, 3-7, 3-3, 3-6, 3-2
#4: {3, 6, 2, 4, 5, 0, 7, 1}
Tricordes: 3-3, 3-6, 3-2, 3-4, 3-9, 3-5, 3-8, 3-7
As demais séries são inversões das anteriores:
#5: {4, 1, 5, 3, 2, 7, 0, 6}
Tricordes: 3-3, 3-6, 3-2, 3-4, 3-9, 3-5, 3-8, 3-7
#6: {4, 5, 0, 7, 1, 3, 6, 2}
Tricordes: 3-4, 3-9, 3-5, 3-8, 3-7, 3-3, 3-6, 3-2
#7: {5, 1, 4, 6, 0, 7, 2, 3}
Tricordes: 3-3, 3-7, 3-8, 3-5, 3-9, 3-4, 3-2, 3-6
#8: {6, 0, 7, 2, 3, 5, 1, 4}
Tricordes: 3-5, 3-9, 3-4, 3-2, 3-6, 3-3, 3-7, 3-8
Exemplo 8: listagem das 8 séries octotônicas oni-intervalares sem tricordes aumentados, diminutos, perfeitos maiores nem menores, com máxima verificação de borda (nível 2).
Estas séries de 8 notas estruturam a ópera “Preço do Perdão” (PAULINYI e MACEDO,
2012). No argumento de Paulinyi, uma viúva regressa do funeral de seu marido. Sua irmã caçula a acompanha até sua casa; porém, carrega um pesado segredo de traição: engravi- dou-se do cunhado pouco antes de seu falecimento, mas pede o perdão da irmã. Entretanto, a viúva conclui exigindo a vida do filho que não teve.
Considerando-se que uma série não é alterada por espelhamentos, inversão nem re- trogradação, sobram duas séries do exemplo 8. Assim, as séries #3 e #4 são atribuídas às personagens “viúva” e “caçula”, respectivamente, na ópera “Preço do Perdão”. Há apenas um único momento em que cada série é apresentada na sua forma original; o restante da obra estrutura-se sobre permutações de sentidos intervalares das séries básicas.6 No exem- plo 9, a série #3 é apresentada pela viúva acompanhada de 8 instrumentos de percussão sem altura definida a partir do compasso 591 com o intuito de enfatizar o momento mais dramático da personagem, quando ela pergunta: “– Foi neste leito de morte que tu mataste a mim gerando essa vida?”. De modo semelhante no exemplo 10, a caçula canta, a partir de c.712, a série #3 acompanhada por outros 8 instrumentos de percussão: “– Passarei a eter- nidade em reparação de meus pecados e dos dele, mas não posso ir sem antes receber o teu perdão”. Nos restante da ópera, os contornos melódicos são harmonizados seguindo o es- quema de tricordes das séries do Exemplo 8.
![]()
177
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182

Exemplo 9: ópera “Preço do Perdão” (PAULINYI e MACEDO, 2012), c.586-598. Iniciada em c.591, a série octotônica oni-intervalar #4 é apresentada pela viúva acompanhada por 8 instrumentos percussivos sem altura definida, iniciados pelos pratos de choque.


Exemplo 10: Em “Preço do Perdão” (idem), c.712-723 apresentam a série octofônica oni-intervalar #3 cantada pela caçula acompanhada por 8 instrumentos percussivos sem altura definida, distintos da outra personagem.
Ainda nessa mesma ópera, encontram-se todas as séries de 6 notas oni-intervalares e sem repetição de tricordes, listadas no Exemplo 11 e utilizadas no intermezzo (Exemplo
12) em duo de percussão sem alturas definidas. As séries em negrito possuem a propriedade adicional de não repetirem tricordes no primeiro nível de verificação de borda. Neste caso, todavia, estas séries não são empregadas para contornos melódicos, mas para determinar contornos rítmicos. Os elementos de cada série, portanto, definem durações de notas, onde começa-se pelo número zero valendo uma semicolcheia, até o número cinco corresponden- do à semínima pontuada. No Exemplo 12, às primeiras 5 notas de percussão 1 em c.798-800, atribuem-se as durações dos elementos da série #1 do Exemplo 11. Cada subsequente grupo![]()
178
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
de 5 notas é associado a uma série diferente do Exemplo 11. Consequentemente, a melodia tímbrica desse trecho caracteriza-se pelo ritmo variado. A ausência de um padrão rítmico estimula o ouvinte a apreciar outros parâmetros musicais da obra.
#1: {0, 5, 1, 4, 2, 3}
Tricordes: 3-4, 3-3, 3-2, 3-1, 3-2, 3-7
#2: {1, 3, 2, 5, 0, 4}
Tricordes: 3-1, 3-2, 3-7, 3-4, 3-3, 3-2
#3: {1, 3, 4, 0, 5, 2}
Tricordes: 3-2, 3-3, 3-4, 3-7, 3-3, 3-1
#4: {1, 4, 0, 5, 3, 2}
Tricordes: 3-3, 3-4, 3-7, 3-2, 3-1, 3-2
#5: {1, 5, 0, 3, 2, 4}
Tricordes: 3-4, 3-7, 3-2, 3-1, 3-2, 3-3
#6: {1, 5, 0, 3, 4, 2}
Tricordes: 3-4, 3-7, 3-3, 3-1, 3-2, 3-3
#7: {2, 0, 5, 1, 4, 3}
Tricordes: 3-7, 3-4, 3-3, 3-2, 3-1, 3-2
#8: {2, 1, 4, 0, 5, 3}
Tricordes: 3-2, 3-3, 3-4, 3-7, 3-2, 3-1
#9: {2, 3, 1, 4, 0, 5}
Tricordes: 3-1, 3-2, 3-3, 3-4, 3-7, 3-2
#10: {2, 3, 5, 0, 4, 1}
Tricordes: 3-2, 3-7, 3-4, 3-3, 3-2, 3-1
#11: {2, 4, 3, 0, 5, 1}
Tricordes: 3-1, 3-3, 3-7, 3-4, 3-3, 3-2
#12: {2, 5, 0, 4, 3, 1}
Tricordes: 3-7, 3-4, 3-3, 3-2, 3-1, 3-3
#13: {3, 0, 5, 1, 2, 4}
Tricordes: 3-7, 3-4, 3-3, 3-2, 3-1, 3-3
#14: {3, 1, 2, 5, 0, 4}
Tricordes: 3-1, 3-3, 3-7, 3-4, 3-3, 3-2
#15: {3, 2, 0, 5, 1, 4}
Tricordes: 3-2, 3-7, 3-4, 3-3, 3-2, 3-1
#16: {3, 2, 4, 1, 5, 0}
Tricordes: 3-1, 3-2, 3-3, 3-4, 3-7, 3-2
#17: {3, 4, 1, 5, 0, 2}
Tricordes: 3-2, 3-3, 3-4, 3-7, 3-2, 3-1
#18: {3, 5, 0, 4, 1, 2}
Tricordes: 3-7, 3-4, 3-3, 3-2, 3-1, 3-2
#19: {4, 0, 5, 2, 1, 3}
Tricordes: 3-4, 3-7, 3-3, 3-1, 3-2, 3-3
#20: {4, 0, 5, 2, 3, 1}
Tricordes: 3-4, 3-7, 3-2, 3-1, 3-2, 3-3
#21: {4, 1, 5, 0, 2, 3}
Tricordes: 3-3, 3-4, 3-7, 3-2, 3-1, 3-2
#22: {4, 2, 1, 5, 0, 3}
Tricordes: 3-2, 3-3, 3-4, 3-7, 3-3, 3-1
#23: {4, 2, 3, 0, 5, 1}
Tricordes: 3-1, 3-2, 3-7, 3-4, 3-3, 3-2
#24: {5, 0, 4, 1, 3, 2}
Tricordes: 3-4, 3-3, 3-2, 3-1, 3-2, 3-7

Exemplo 11: séries hexatônicas oni-intervalares sem repetição de tricordes. Em negrito estão as séries que não possuem tricordes repetidos na primeira verificação de borda (nível 1). Não há séries assim com clausura total de tricordes (verificação de borda em nível 2).
![]()
179
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182

Exemplo 12: c.798-804, intermezzo da ópera “Preço do Perdão”, é o início de um duo de percussão sem alturas definidas. Percussão 1 possui uma melodia tímbrica a cujas notas são atribuídas durações de séries hexatônicas oni-intervalares do Exemplo 11.
Este intermezzo, além de ilustrar a geração de séries oni-intervalares de 6 elementos com propriedades harmônicas agregadas em diversos graus de clausura, apresenta uma uti- lização paramétrica relacionada, antes, às durações de notas, e não às suas alturas.
Conclusão e possíveis desdobramentos à investigação
Embora seja um assunto centenário, a oni-intervalaridade sofreu certa estagnação acadêmica por causa de premissas e algoritmos restritivos nas décadas de 1960 e 1970. Este texto propõe uma retificação teórica e um aprimoramento no algoritmo gerador de séries oni-intervalares: como retificação, a necessidade de se evitar equivalência de oitavas e seu consequente “endireitamento” de séries; como melhoramento, a incorporação de proprieda- des adicionais às séries, não limitadas a 12 elementos. Tais propriedades podem ser, primei- ramente, relacionadas à presença e exclusão de tricordes, como ilustrado neste artigo. Um possível desdobramento desta linha de pesquisa seria considerar-se a verificação de outras propriedades, como campos harmônicos de variado número de notas.
O desenvolvimento computacional do algoritmo gerador de séries oni-intervalares serve para acelerar ou catalisar procedimentos composicionais; por outro lado, o intérpre- te e o ouvinte não necessitam de qualquer auxílio computacional para apreciar as proprie- dades intervalares incorporadas às séries. Para demonstrar isso, foram apresentados três exemplos musicais, onde apenas o primeiro era dodecafônico. Os dois exemplos seguintes ilustram a aplicação do algoritmo para séries com diversificado número de notas, e até mes- mo para contornos rítmicos em vez de contornos melódicos.
Agradecimentos institucionais
Agradeço à Orquestra Sinfônica do Teatro Nacional Claudio Santoro em Brasília, que me autorizou realizar doutoramento na Universidade de Évora. Agradeço a acolhi- da deste projeto de investigação pela Unidade de Investigação em Música e Musicologia (UnIMeM) em Portugal.![]()
180
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
Notas
1 A literatura sobre cognição pouco menciona sobre semelhança a outros intervalos, mesmo aqueles múltiplos inteiros da frequência fundamental.
2 Nos primórdios da computação, encontravam-se autores que utilizavam a letra T ou A para Sib, e letra E ou B
para Si, com o intuito de utilizar um caractere em vez de dois algarismos.
3 Do inglês “all-interval row”. Agradeço ao Dr. Christopher Bochmann, diretor dos departamentos de artes da Universidade de Évora, pela cunhagem deste termo em português e por mostrar a incongruência do conceito de dodecafonismo à não equivalência de oitavas.
4 Tomando a definição de “dodecafônico” pelo uso dos 12 sons do total cromático de uma oitava heptatônica, tem-
-se que a Suíte Lírica não é uma simples caracterização de dodecafonismo porque sua série ultrapassa a oitava heptatônica, transbordando o trecho musical em 21 semitons.
5 Neste caso, o tricorde 3-4 seria o subconjunto faltante para completar a representatividade das 12 categorias listadas for Allen Forte. Mesmo avaliando o segundo nível de clausura, 3-4 não está presente dado que {6, 4, 7}
= 3-2, tricorde que estaria repetido nesta série.
6 A totalidade de permutações de sentidos intervalares de uma mesma série constitui a onicontornidade.
Referências
BAUER-MENGELBERG, Stefan; FERENTZ, Melvin. On Eleven-Interval Twelve-Tone Rows. Perspectives of New Music, v.3, n.2, Spring-Summer 1965, p. 93-103. Disponível em: <http:// www.jstor.org/stable/832507>. Acesso em; 25/1/2011.
BERG, Alban. Lyrische Suite. 1. ed. Viena: Universal Edition, 1927. Plate U.E. 8780/W.Ph.V.
173. Disponível em: <http://imslp.org/wiki/Lyrische_Suite_(Berg,_Alban)>, direto em: <http://
imslp.org/wiki/Special:ImagefromIndex/19115>. Acesso em; 16/6/2011.
FORTE, Allen. The structure of atonal music. New Haven: Yale University Press, 1973. MORRIS, Robert D. Equivalence and Similarity in Pitch and Their Interaction with PCSet
Theory. Journal of Music Theory, Duke University Press on behalf of the Yale University Department of Music, v.39, n.2 (Autumn), 1995, p. 207-243. Disponível em: <http://www.jstor. org/stable/843967>. Acesso em; 14/05/2011.
MORRIS, Robert; STARR, Daniel. The Structure of All-Interval Series. Journal of Music Theory, Duke University Press on behalf of the Yale University Department of Music, v.18, n.2, 1974, p. 364-389. Disponível em: <http://www.jstor.org/stable/843642>. Acesso em;
25/01/2011.
PAULINYI, Zoltan; MACEDO, Ester. Biblioteca: ópera de câmara para soprano e baixo-barí- tono. Suíça: MusicaNeo, 2011b. Duração: 45 minutos. Disponível em: <http://paulinyi.musi- caneo.com/sheetmusic/sm-66488_biblioteca_library _chamber_opera_for_soprano_and_bass-
-baritone_full_score.html>. Acesso em; 11/5/2011. Vídeo da estreia em: <http://youtu.be/
hkWFWlgmYv4>.
PAULINYI, Zoltan; MACEDO, Ester. Preço do perdão: ópera para duas sopranos. Suíça: MusicaNeo. 2012. Duração: 50 minutos. Disponível em: <http://paulinyi.musicaneo.com/ sheetmusic/sm-159993_ price_of_forgiveness_ preco_do_ perdao_opera_for_2_sopranos_and_ chamber_ensemble_f.html>. Acesso em; 22/7/2012. Vídeo da estreia: <http://youtu.be/s5FcU- vJ7uR0>. Da reapresentação: <http://youtu.be/XtYTsQYytHk>
![]()
181
![]()
PAULINYI, Z.Séries Notáveis Oni-Intervalares. Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 171-182
Leitura recomendada
OLIVEIRA, João Pedro. “Teoria Analítica da Música do Séc. XX”. Fundação Calouste Gulbenkian, Lisboa: 1998.
![]()
![]()
![]()
182
![]()