

Revista Música Hodie, Goiânia - V.14, 238p., n.1, 2014
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
Aluizio Arcela (Universidade de Brasília, Brasília, DF)
A Type of Counterpoint Which Exists in the Space-time of Intervals
A extração de melodias elementares bem formadas do interior de intervalos musi- cais1 é um assunto abordado em ARCELA, 2012, onde se propõe a análise da épura de ár- vores de tempos2 como critério norteador para se obter um posicionamento significativo do objeto intervalar3 no espaço euclidiano. Posicionamento significativo é aquele em que se produz uma melodia que poderá ser considerada como um fragmento autêntico de música, quando avaliada por um número razoável de ouvintes, sobretudo músicos e apreciadores da música em geral. O conceito de espaço-tempo intervalar4 aqui introduzido se sustenta na combinação do espaço euclidiano relativo aos intervalos musicais com o tempo estruturado por meio das árvores de tempos.
Para a criação de vozes completas com esta técnica, é necessário proceder-se com o cálculo de uma sucessão de frases – isto é, melodias elementares – que se decifram por meio das mencionadas épuras. Neste sentido, embora haja diferentes maneiras de se fazer o cálculo e a emenda das frases melódicas, uma delas parece ser mais forte. Trata-se da téc- nica de se dispor em contiguidade uma sequência de melodias geradas por objetos interva- lares de segunda ordem, isto é, objetos representantes de intervalos musicais secundários, que se criam nas próprias árvores de tempos pertencentes a um objeto intervalar primal5. Desta forma, produzem-se sucessivas transformações algébrico melódicas, as quais propi- ciarão um crescimento espontâneo na dimensão melódica, isto por meio de frases que têm entre si um certo grau de parentesco estrutural. Portanto, é este procedimento que poderá levar uma voz construída a ter o predicado de ser bem formada.
No caso do presente artigo, a abordagem limita-se às manifestações polifônicas mais primitivas no interior do mencionado espaço-tempo intervalar. Especificamente, o que
se discute são as bases polifônicas de um sistema composicional que faz uso do conteúdo e
Revista Música Hodie, Goiânia - V.14, 238p., n.1, 2014 Recebido em: 18/11/2013 - Aprovado em: 15/03/2014
![]()
49
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
da topologia6 de árvores de tempos combinadas com a cinemática de objetos intervalares7. O primeiro e mais importante comportamento contrapontístico espontâneo que aí se obser- va ocorre quando o intervalo está em equilíbrio (v. ARCELA, 2008).
De acordo com o modelo denominado objeto intervalar, todo intervalo pode assu- mir dois estados acústicos, quais sejam, o estado alto e o estado baixo, havendo em cada um deles uma determinada coleção de padrões rítmicos característicos. O posicionamento sistemático e apurado do intervalo no espaço euclidiano tridimensional conferirá melodias a esses padrões, que são estruturas de tempos, de alturas (pitch) e de níveis de intensidade acústica, de tal maneira que se podem calcular melodias distintas em cada um dos estados.
No caso específico do equilíbrio intervalar8 – que é uma situação atingida por uma
parametrização que coloca o intervalo bem no limite entre os estados alto e baixo –, haverá espontaneamente uma ação recíproca de duas melodias concorrentes, as quais estabelece- rão um contraponto bem formado e com grau de coesão relevante9, a depender, entretanto, de se determinar um posicionamento significativo para o objeto intervalar.
Evidentemente que há neste processo de construção contrapontística diferenças básicas com relação às técnicas de contraponto que se conhecem historicamente, isto des- de o tratado de Gioseffo Zarlino escrito no século XVI (v. ZARLINO, 1968), até os textos do século XX (por exemplo, KRONEK, 1940; SCHOENBERG, 1963; OWEN, 1992). No caso do contraponto com as árvores de tempos, as duas vozes (cada qual contendo uma única fra- se melódica, que é proveniente do respectivo objeto intervalar – em um dos estados alto ou baixo) serão superpostas por inteiro no espaço-tempo intervalar, e não nota a nota. O fato de elas se associarem naturalmente advém da relação de parentesco estrutural que há entre as duas, a qual se deve à condição de representarem em conjunto as duas faces (acústico mu- sicais) de um mesmo intervalo.
Os ritmos que se podem extrair das florestas de tempos resultam da circunstân- cia temporal, isto é, eles dependem tanto da ordem cronológica dos nodos das árvores – no- dos estes que se constituem nos chamados eventos intervalares – quanto das durações des- ses nodos. Os eventos intervalares traduzem-se em notas musicais que surgem ao longo de um período do intervalo, denominado –, cuja extensão mede 2mn passos (ARCELA, 2013, Chapter 2). Ao longo de um período τ, coleta-se uma sequência de durações da floresta por meio de um tipo especial de percurso em árvores10 que se denomina “primeiro em largura”, o qual se resume em caminhar-se nível a nível nas árvores, visitando-se sequencialmente os nodos contíguos de um mesmo nível, sempre da esquerda para a direita, e com início no nodo raiz da primeira árvore de tempos (ARCELA, 2014).
Evidentemente que, neste sistema musical, haverá infinitas melodias possíveis para um número finito de ritmos decifráveis (ver LAMUS, 2013b), as quais se calculam quan- do os eventos intervalares11 acima mencionados são considerados não só na circunstância temporal, mas também na sua realidade geométrica, isto é, como pontos do espaço euclidia- no. Mais especificamente, cada um desses pontos poderá ser convertido em nota musical, já que todos eles possuem posição e velocidade próprias, sendo ambas calculáveis por meio da cinemática do movimento intervalar, movimento este que resulta da combinação de dois movimentos periódicos12, sendo, um deles, um movimento harmônico simples – justamente aquele com maior força da altura13 e que, por esta razão, define o estado do intervalo – e, o outro, um movimento circular e uniforme.![]()
50
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
Uma propriedade do espaço-tempo intervalar de grande impacto para os sistemas de composição é que apenas algumas melodias obtidas com esses sistemas apresentam con- teúdo musical suficiente para serem consideradas verdadeiras ou, mais precisamente, viá- veis. Isto ocorre porque as melodias viáveis são singularidades do espaço-tempo intervalar, isto é, são raridades em meio a uma infinidade de melodias falsas. E é neste contexto que a busca por melodias viáveis torna-se uma das etapas principais, e talvez a mais complexa, do método de composição que se baseia nas árvores de tempos14.
A melodia estará pronta para ser calculada depois que o objeto intervalar estiver posicionado e orientado no espaço euclidiano tridimensional, lugar em que as grandezas cinemáticas do movimento combinado devem ser computadas a cada nodo das árvores (do particular intervalo), de modo a fornecer os dados restantes, isto é, altura e intensidade. Conhece-se antecipadamente a duração de cada nota, porque ela sempre será dada pelo pró- prio conteúdo numérico do nodo (v. ARCELA, 2013, Chapter 6), que representa o seu tempo de existência, isto é, a sua vigência na melodia. Deste modo, a extinção de um nodo coinci- dirá com o surgimento do nodo subsequente.
De acordo com o exposto acima, para se dar início ao cômputo de uma melodia, os parâmetros principais do objeto intervalar – juntamente com as três transformações bási- cas, quais sejam, posição, orientação e fatores melódicos – já devem estar valorados. A po- sição do objeto intervalar é definida pelas coordenadas cartesianas de seu centro [px py pz], enquanto que a orientação é definida por meio dos chamados ângulos de rotação de Euler [ρx ρy ρz] em torno dos eixos x, y e z, respectivamente. Os fatores melódicos, isto é, fator de andamento, fator de transposição e fator de dinâmica, constituem a terceira e última trans- formação básica (ver ARCELA, 2014).
Do ponto de vista do modelo das árvores de tempos (ARCELA, 2013), que é o se- gundo estágio do modelo para o intervalo, o que se denomina contraponto intervalar é a ação recíproca de duas melodias concorrentes que se estabelecem quando o intervalo mu- sical encontra-se em equilíbrio (ver ARCELA, 2008, Section 2.2). A decifração contrapon- tística é, pois, algo pertencente ao domínio da composição formal15, tanto quanto o são os métodos descritos por alguns autores, como XENAKIS, 1957; HILLER, 1964; LINDBLOM e SUNDBERG, 1969; LERDHAL e JAKENDOFF, 1983.16
De acordo com o modelo das árvores de tempos, em um intervalo musical justo, cuja razão de frequências é [m:n] – sendo m e n números inteiros primos entre si – há n rit- mos passíveis de decifração no estado baixo, enquanto que no estado alto há m ritmos. E se há infinitas melodias que podem ser atribuídas a cada um desses ritmos que se definem nos estados intervalares, conforme mencionado acima na Seção 2, será porque há infinitas maneiras de se posicionar e orientar o objeto intervalar no espaço euclidiano. Quando o in- tervalo se encontra no estado baixo e, além disto, está devidamente, ou de alguma maneira, posicionado e orientado no espaço, define-se aí uma única melodia. Da mesma forma, estan- do o intervalo no estado alto, criar-se-á uma outra melodia, também única.
Já no equilíbrio – que é uma condição singular e própria de cada intervalo – sur- gem duas melodias concorrentes, supostamente como se fossem nascidas uma para a outra. A despeito da importância deste fato para a construção formal da música, especialmente da música polifônica, não se pode dizer que se trata de um resultado de todo surpreendente. Em última análise, a existência dessas duas melodias simultâneas é a condição mais pro-![]()
51
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
funda para que o intervalo esteja verdadeiramente em equilíbrio. Portanto, é na condição de equilíbrio que se estabelece o assim chamado contraponto intervalar.
Em suma, o equilíbrio é uma coexistência de dois objetos intervalares superpostos, cujos parâmetros são conjugados. Isto é, os parâmetros do movimento harmônico simples de um objeto correspondem aos parâmetros do movimento circular uniforme do outro obje- to, e vice-versa. Por definição, os dois objetos coexistentes no equilíbrio intervalar são tais que um deles pertence ao estado baixo, enquanto o outro pertence ao alto (ver Seção 4 sobre o ajuste infinitesimal na proporção de amplitudes). Estes dois objetos que modelam e dão vida ao equilíbrio são aqui denominados objetos intervalares conjugados.
Uma vez que os movimentos circulares podem girar em sentido horário ou em sen- tido anti-horário, a ordenação cronológica das notas de cada uma das duas melodias pode- rá ser direta ou retrógrada, considerando-se que há quatro possíveis conjugações para cada par de melodias intervalares (alto e baixo) encontradas. Isto é, haverá as conjugações DD (ordenação direta × ordenação direta), DR (ordenação direta × ordenação retrógrada), RD (ordenação retrógrada × ordenação direta), e a RR (ordenação retrógrada × ordenação retró- grada). Assume-se que uma dada melodia será de ordenação retrógrada se o movimento cir- cular uniforme do respectivo objeto intervalar tiver o sentido horário. E, portanto, se o mo- vimento circular tiver o sentido anti-horário, a melodia será de ordenação direta.
Uma última propriedade do contraponto intervalar a ser observada consiste no fato de que as duas melodias se iniciam em momentos distintos, uma vez que haverá sempre uma diferença de tempo entre o surgimento da primeira nota do objeto conjugado baixo e o surgimento da primeira nota do objeto conjugado alto. E como ambas as melodias têm a mesma duração – correspondendo justamente a um período do objeto intervalar – a melodia tardia continuará por mais um pouco após o término da melodia pontual. Isto é, ela pros- seguirá soando sozinha pelo mesmo tempo que esperou para entrar. A este respeito, con- forme ilustram os exemplos abaixo, as tais melodias concorrentes se iniciam naturalmen- te em momentos distintos, às vezes próximos, às vezes distantes, a depender dos valores das ordens de frequência m e n, e dos ângulos de fase inicial dos movimentos harmônicos simples dos dois objetos intervalares conjugados que constituem o intervalo em estado de equilíbrio.![]()
![]()
![]()
![]()
Com o fim de ilustrar a existência de estruturas musicais no espaço-tempo dos in- tervalos, descrevem-se a seguir três exemplos contrapontísticos C1, C2 e C3, sendo a descri- ção do contraponto C1 um pouco mais detalhada do que a dos demais, especialmente na ilustração da decifração dos ritmos, assim como na determinação de uma melodia viável para um dado ritmo decifrado. Nos dois exemplos subsequentes, essas duas etapas iniciais são análogas às do primeiro exemplo e, portanto, são omitidas.
Neste primeiro exemplo, estuda-se o intervalo de uma terça menor [5:6] cujo pri- meiro objeto intervalar conjugado – aquele que se encontra ligeiramente no estado baixo – é tal que os seus parâmetros, quais sejam, posição do centro [px py pz], orientação segundo ân- gulos de Euler [ρx ρy ρz], assim como as ordens de frequência m e n da razão intervalar [m:n], como também a amplitude (a) do movimento harmônico simples (MHS), a sua fase inicial (ϕ), juntamente com o raio (b) do movimento circular uniforme (MCU), o seu giro inicial (θ), e ainda os fatores melódicos kA para o andamento, kT para transposição e kD para a di- nâmica, estão mostrados na Tabela 1. Este primeiro objeto intervalar contém a melodia M1B![]()
52
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
do contraponto C1. Sendo a relação de equilíbrio dada por (ver ARCELA, 2008, Section 2.2), o valor do raio (b) do MCU será um pouco reduzido (teoricamente por um infinitésimo), de tal maneira que o objeto pertencerá ligeiramente ao estado baixo.
Tabela 1: Primeiro objeto intervalar conjugado de uma terça menor [5:6] ligeiramente no estado baixo.
a | m | ϕ | b | n | θ | px | py | pz | ρx | ρy | ρz | kA | kT | kD | sentido | |
MHS | 24 | 5 | 46 | |||||||||||||
MCU | 16,665 | 6 | 244 | Anti-horário | ||||||||||||
Posição | –12 | –40 | –18 | |||||||||||||
Orientação | 174 | 209 | 244 | |||||||||||||
Fatores | 7 | 7 | 2 |
Para se obter o segundo objeto intervalar conjugado desta terça menor [5:6], consi- dera-se mais uma vez a relação de equilíbrio am2 = bn2 como ponto de partida, e aumenta-
-se um pouco (teoricamente um infinitésimo) o valor do parâmetro b – correspondente ao raio do MCU do primeiro objeto – de modo a tornar-se agora a amplitude do novo MHS. Assim, o segundo objeto conjugado pertencerá ligeiramente ao estado alto. Em seguida, o valor do parâmetro a, correspondente à amplitude do MHS do primeiro objeto conjugado, deverá torna-se o raio do novo MCU, cujo sentido de rotação é horário, de modo que a orde- nação melódica correspondente será retrógrada. Os parâmetros deste segundo objeto inter- valar conjugado da terça menor [5:6] encontram-se na Tabela 2. A melodia M1A do contra- ponto C1 está contida neste objeto.![]()
Tabela 2: Segundo objeto intervalar conjugado de uma terça menor [5:6] ligeiramente no estado alto.
a | m | ϕ | b | n | θ | px | py | pz | ρx | ρy | ρz | kA | kT | kD | sentido | |
MCU | 24 | 5 | 46 | Horário | ||||||||||||
MHS | 16,667 | 6 | 244 | |||||||||||||
Posição | –12 | –40 | –18 | |||||||||||||
Orientação | 174 | 209 | 244 | |||||||||||||
Fatores | 7 | 7 | 2 |
Para se compor um contraponto intervalar, a primeira consideração consiste em se identificar o conjunto de árvores em cada um dos estados alto e baixo, uma vez que o estado de equilíbrio – conforme mencionado na Seção 3 e ilustrado nas Tabelas 1 e 2 – consolida-se na convivência espaço temporal de dois objetos quase iguais do ponto de vista de seus pa- râmetros, mas que são na realidade objetos intervalares em estados diferentes. Isto causará árvores de tempos diferentes em cada um dos dois objetos, assim como as geometrias serão distintas e, portanto, os ritmos e as melodias serão distintos e contrapontísticos.
Desta maneira, neste primeiro exemplo, verifica-se que há três árvores de tempos na floresta A1 de uma terça menor justa [5:6] no estado baixo, na sua terceira mutação (v. ARCELA, 2013, Chapter 5), conforme ilustra a Figura 1. Tal floresta A1 é uma das seis hie- rarquias temporais que se podem criar no interior de uma terça menor-5:6 no estado baixo.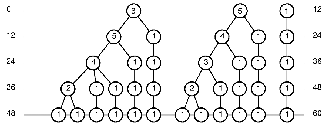
Figura 1: Floresta A1 de árvores de tempos do intervalo 5:6-terça maior no estado baixo, 3ª mutação, d0 = 12.
![]()
53
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
A coleta de notas na floresta A1 se inicia no nodo raiz da árvore mais à esquerda, isto é, a duração {6}, que é seguida pela raiz da segunda árvore {5} e, então, como último elemento do primeiro nível (ou geração) da floresta, o nodo raiz da terceira árvore {1} é coletado. Em se- guida, considera-se a segunda geração de durações, de modo que os dois nodos descendentes
{5 1} da primeira raiz são coletados, aí então tomam-se os descendentes {4 1} da raiz da segun- da árvore e, finalmente neste segundo nível, toma-se o descendente {1} da terceira árvore. Em seguida, a terceira geração produz {4 1 1}, {3 1 1} e {1}. A quarta geração por sua vez produz
{2 1 1 1 1}, {2 1 1 1} e {1}. Finalmente, a quinta geração produz {1 1 1 1 1 1}, {1 1 1 1 1} e {1}.
Uma vez que o contraponto C1 é uma conjugação contrapontística do tipo RD, a voz baixo estará sob ordenação retrógrada. Desta maneira, quando se unem todas as gerações enumeradas acima, e inverte-se a ordem dos termos, obtém-se a sequência de durações D1B
= {1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 2 1 1 1 3 1 1 4 1 1 4 1 5 1 5 6} para as notas da voz baixo do contraponto C1.
Assumindo-se que a menor duração na sequência D1B – isto é, a unidade {1} – corresponde a uma semicolcheia, produz-se então a estrutura rítmica R1B que se exibe na Figura 2 para a voz baixo do contraponto.![]()
Figura 2: Ritmo R1B definido pela sequência de durações D1B.
Levando-se em conta que as notas de R1B correspondem a pontos do objeto intervalar cujas posições e velocidades são conhecidas, podem-se calcular para cada uma delas as gran- dezas acústicas correspondentes (v. ARCELA, 2013, Chapter 6, Calculating Notes), de manei- ra que se podem agregar a cada elemento da sequência de durações os devidos valores de al- tura e intensidade, a fim de se completar o cômputo de cada nota. Graças a esses cálculos, a estrutura rítmica R1B poderá ser mapeada para a melodia M1B, conforme se exibe na Figura 3.
Figura 3: Melodia M1B para o ritmo R1B.
Para o segundo objeto – que é do estado alto, e é conjugado ao objeto do estado baixo
– há duas árvores de tempos na floresta Ω1, neste caso de uma terça menor justa [5:6] na sua terceira mutação, conforme ilustra a Figura 4. Tal floresta Ω1 é uma das cinco hierarquias temporais que se podem criar no interior de uma terça menor-5:6 no estado alto.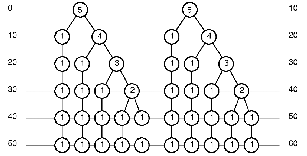
Figura 4: Floresta Ω1 de árvores de tempos do intervalo 5:6-terça maior no estado alto, 5ª mutação, d0 = 16.
![]()
54
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
A coleta de notas na floresta Ω1 se inicia no nodo raiz da árvore mais à esquerda, isto é, a duração {5}, que é sucedida pela raiz da segunda árvore {5}. Em seguida, conside- ra-se a segunda geração de durações, de modo que os dois nodos descendentes {1 4} da pri- meira raiz são coletados, quando então se tomam os descendentes {1 4} da raiz da segunda árvore. A terceira geração produz {1 1 3} e {1 1 3}. A quarta geração, por sua vez, produz {1
1 1 2} e {1 1 1 2}. A quinta geração produz {1 1 1 1 1} e {1 1 1 1 1}. E, finalmente, a sexta ge- ração produz {1 1 1 1 1} e {1 1 1 1 1}.
Outra vez, considerando-se que, por construção, C1 é uma construção contrapon- tística do tipo RD, a voz alto, diferentemente da voz baixo descrita acima, estará sob orde- nação direta. Desta maneira, quando se unem as gerações de durações extraídas da floresta Ω1, obtém-se a sequência de durações D1A = {{4} 5 5 1 4 1 4 1 1 3 1 1 3 1 1 2 1 1 1 1 2 1 1 1
2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1} para as notas da voz alto do contraponto.
Assumindo-se que a menor duração na sequência D1A – isto é, a unidade {1} – corresponde a uma semicolcheia, produz-se então a estrutura rítmica R1A que se exibe na Figura 5 para a voz alto do contraponto.![]()
Figura 5: Ritmo R1A definido pela sequência de durações D1A.
De modo semelhante ao empregado na voz baixo, uma melodia M1A que seja viá- vel para este ritmo R1A deverá ser calculada. A primeira duração D1A, que se representa por
{{4}...}, indica que M1A é a melodia tardia, uma vez que a primeira nota da melodia alto se inicia com um retardo de {4} unidades de tempo (passos) relativamente ao início da primei- ra nota da melodia baixo M1B. Esta é a razão da pausa de semínima ao início do ritmo R1A. A Figura 6 mostra a melodia M1A da voz alto, melodia esta que é indissociável de M1B da voz baixo, considerando-se que se trata de sua contrapartida intervalar.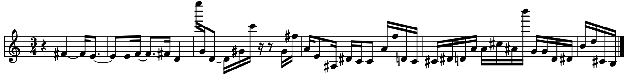
Figura 6: Melodia M1A para o ritmo R1A.
Em síntese, a partir das sequências de durações produzidas pelas florestas A1 e Ω1, e do emprego devido da cinemática intervalar, duas melodias são construídas, isto é, M1B e M1A. A Figura 7 mostra a disposição em contraponto destas melodias calculadas para cada um dos estados alto e baixo do intervalo, depois que o objeto intervalar é posicionado no espaço. A escrita se faz em cinco compassos em uma fórmula de compasso de 3/4, uma vez que a duração total da sequência é de 60 passos de tempo (τ = 2mn = 2 × 5 × 6). Em outras palavras, dispondo-se 12 passos (isto é, três semínimas) em cada compasso, todo o contra- ponto C1 estará acomodado em cinco compassos.![]()
55
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65

Figura 7: ???????????????????????????????????
Relativamente ao exemplo anterior, este contraponto C2 será descrito de forma mais abreviada, uma vez que os procedimentos iniciais são semelhantes. Fica implícito que os ritmos R2B e R2A serão devidamente decifrados, assim como as melodias M2B e M2A haverão de ser calculadas.
Os parâmetros do primeiro objeto intervalar do equilíbrio primal de uma segunda maior [8:9], quais sejam, posição, orientação, assim como os números (m e n) da razão inter- valar [m:n], amplitude (a) do MHS, o ângulo de fase inicial (ϕ), juntamente com o raio (b) do MCU, o ângulo de giro inicial (θ), e os fatores melódicos (kA, kT e kD) são mostrados na Tabela
3. A melodia M2B está contida neste objeto intervalar. Sendo a relação de equilíbrio dada por am2 = bn2, o raio b do MCU será um pouco reduzido (teoricamente por um infinitésimo), de tal maneira que o objeto pertencerá ligeiramente ao estado baixo.![]()
Tabela 3: Primeiro objeto intervalar conjugado de uma segunda maior [8:9] ligeiramente no estado baixo.
a | m | ϕ | b | n | θ | px | py | pz | ρx | ρy | ρz | kA | kT | kD | sentido | |
MHS | 24 | 8 | –1 | |||||||||||||
MCU | 18,961 | 9 | 244 | Anti-horário | ||||||||||||
Posição | 24 | –2 | 15 | |||||||||||||
Orientação | 232 | 197 | 255 | |||||||||||||
Fatores | 11 | 7 | 1 |
Quanto ao segundo objeto intervalar conjugado, considera-se mais uma vez a rela- ção de equilíbrio am2 = bn2 como ponto de partida, e aumenta-se um pouco (teoricamente um infinitésimo) o valor do parâmetro b – correspondente ao raio do MCU do primeiro ob- jeto – de modo a tornar-se agora a amplitude do novo MHS, de tal maneira que este segundo objeto pertencerá ligeiramente ao estado alto. O valor do parâmetro a, correspondente à am- plitude do MHS do primeiro objeto conjugado, tornar-se-á o raio do novo MCU, cujo senti- do de rotação é anti-horário, de modo que a ordenação melódica correspondente será direta. Os parâmetros deste segundo objeto intervalar conjugado da segunda maior [8:9] estão na Tabela 4. A melodia M2A do contraponto C2 está contida neste objeto intervalar.![]()
56
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
Tabela 4: Segundo objeto intervalar conjugado de uma segunda maior [8:9] ligeiramente no estado alto.
a | m | ϕ | b | n | θ | px | py | pz | ρx | ρy | ρz | kA | kT | kD | sentido | |
MCU | 24 | 8 | –1 | Anti-horário | ||||||||||||
MHS | 18,963 | 9 | 244 | |||||||||||||
Posição | 24 | –2 | 15 | |||||||||||||
Orientação | 232 | 197 | 255 | |||||||||||||
Fatores | 11 | 7 | 2 |
Neste caso de uma segunda maior justa [8:9] como objeto primal, há três árvores de tempos na floresta A2 no estado baixo natural, na sua segunda mutação, conforme ilustra a Figura 8. Tal floresta A2 é uma das nove hierarquias temporais que se podem extrair do in- terior de uma segunda maior-8:9 no estado baixo.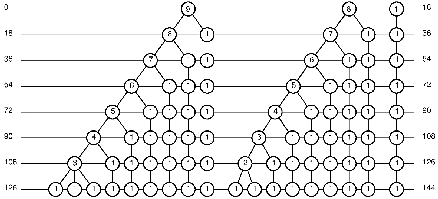
Figura 8: Floresta A2 de árvores de tempos do intervalo 8:9-segunda maior no estado baixo, 2ª mutação, d0 = 17.
Assim como se fez na floresta A1 acima, a coleta de notas na floresta A2 se inicia no nodo raiz da árvore mais à esquerda que, neste caso, é a duração {9}, a qual é seguida pela raiz da segunda árvore {8} e, então, como último elemento do primeiro nível (ou ge- ração) da floresta, o nodo raiz da terceira árvore {1} é coletado. Em seguida, considera-se a segunda geração de durações, de modo que os dois nodos descendentes {8 1} da primeira raiz são coletados. Tomam-se então os descendentes {7 1} da raiz da segunda árvore e, fi- nalmente neste segundo nível, toma-se o descendente {1} da terceira árvore. Em seguida, a terceira geração produz {7 1 1}, {6 1 1} e {1}. A quarta geração por sua vez produz {6 1 1 1},
{5 1 1 1} e {1}. A quinta geração produz {5 1 1 1 1}, {4 1 1 1 1} e {1}. A sexta geração produz
{4 1 1 1 1 1}, {3 1 1 1 1 1} e {1}. A sétima geração produz {3 1 1 1 1 1 1}, {2 1 1 1 1 1 1} e {1}. Finalmente, a oitava geração produz {1 1 1 1 1 1 1 1 1}, {1 1 1 1 1 1 1 1} e {1}.
Já no caso do estado alto mostrado na Figura 9, há duas árvores de tempos na flores- ta Ω2 de uma segunda maior justa [8:9] no estado alto, na sua segunda mutação. Tal flores- ta Ω2 é uma das oito hierarquias temporais que se podem criar no interior de uma segunda
maior justa [8:9] no estado alto.![]()
57
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
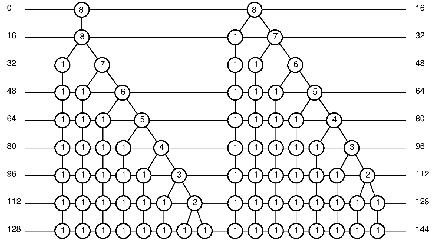
Figura 9: Floresta Ω2 de árvores de tempos do intervalo 8:9-segunda maior no estado alto, 1ª mutação, d0 = 18.
Da mesma forma, assim como se procedeu com a floresta Ω1 acima, a coleta de no- tas na floresta Ω2 se inicia no nodo raiz da árvore mais à esquerda, isto é, a duração {8}, que é sucedida pela raiz {8} da segunda árvore, chamada árvore telescópica17. Em seguida, considera-se a segunda geração de durações, de modo que o nodo descendentes {8} da pri- meira raiz é coletado, aí então tomam-se os descendentes {1 7} da raiz da segunda árvore. A terceira geração produz {1 7} e {1 1 6}. A quarta geração por sua vez produz {1 1 6} e {1 1
1 5}. A quinta geração produz {1 1 1 5} e {1 1 1 1 4}. A sexta geração produz {1 1 1 1 4}, {1
1 1 1 1 3}. A sétima geração produz {1 1 1 1 1 3} e {1 1 1 1 1 1 2}. A oitava geração produz
{1 1 1 1 1 1 2} e {1 1 1 1 1 1 1 1}. E, finalmente, a nona geração produz {1 1 1 1 1 1 1 1} e {1
1 1 1 1 1 1 1}.
Figura 10: Contraponto C2 decifrado no interior de uma segunda maior (8:9) em equilíbrio. (Áudio on-line disponível em
LAMUS 2013a.)
Por construção, o contraponto C2 é do tipo DD, (direta × direta). Com as sequências de durações produzidas pelas florestas A2 e Ω2, dois padrões rítmicos R2B e R2A são formados![]()
58
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
a partir das durações dos respectivos eventos. A Figura 10 mostra a disposição das melo- dias M2B e M2A calculadas para cada um desses dois padrões rítmicos, isto depois que o ob- jeto intervalar é posicionado no espaço. A escrita se faz em doze compassos em uma fórmu- la de compasso de 6/8, uma vez que a duração total da sequência é de 144 passos de tempo. Em outras palavras, dispondo-se 12 passos (isto é, seis colcheias) em cada compasso, todo o contraponto C2 estará acomodado em doze compassos.
Também neste terceiro e último caso contrapontístico C3, a descrição será mais abreviada, uma vez que os procedimentos iniciais são semelhantes. Fica implícito que os ritmos R3B e R3A serão decifrados, assim como as melodias M3B e M3A serão calculadas.
Os parâmetros do primeiro objeto intervalar conjugado de uma décima sexta dimi- nuta [3:13], quais sejam, posição, orientação, assim como razão intervalar [m:n], amplitude (a) do MHS, fase inicial (ϕ), juntamente com o raio (b) do MCU, o giro inicial (θ), e os fato- res melódicos (kA, kT e kD) estão na Tabela 5. Este objeto intervalar contém a melodia M3B. Sendo a relação de equilíbrio dada por am2 = bn2, o valor do raio b do MCU será um pouco reduzido (teoricamente por um infinitésimo), de tal maneira que o objeto pertencerá ligei- ramente ao estado baixo.
Tabela 5: Primeiro objeto intervalar conjugado de uma décima sexta diminuta [3:13] ligeiramente no estado baixo.
a | m | ϕ | b | n | θ | px | py | pz | ρx | ρy | ρz | kA | kT | kD | sentido | |
MHS | 45 | 3 | 127 | |||||||||||||
MCU | 2,395 | 13 | –1 | Anti-horário | ||||||||||||
Posição | 11 | 27 | 18 | |||||||||||||
Orientação | 128 | 221 | 59 | |||||||||||||
Fatores | 6 | 7 | 2 |
Quanto ao segundo objeto intervalar conjugado deste terceiro contraponto, conside- ra-se outra vez a relação de equilíbrio am2 = bn2 como ponto de partida, e aumenta-se um pouco (teoricamente um infinitésimo) o valor do parâmetro b – correspondente ao raio do MCU do primeiro objeto – de modo a tornar-se agora a amplitude do novo MHS, de tal ma- neira que este segundo objeto pertencerá ligeiramente ao estado alto. O valor do parâmetro a, correspondente à amplitude do MHS do primeiro objeto, tornar-se-á o raio do novo MCU, cujo sentido de rotação é anti-horário, de modo que a ordenação melódica correspondente será direta. Os parâmetros deste segundo objeto intervalar conjugado da décima sexta di- minuta [3:13] estão na Tabela 6. A melodia M3A está contida neste segundo objeto intervalar.![]()
Tabela 6: Segundo objeto intervalar conjugado de uma décima sexta diminuta [3:13] ligeiramente no estado alto.
a | m | ϕ | b | n | θ | px | py | pz | ρx | ρy | ρz | kA | kT | kD | sentido | |
MCU | 45 | 3 | 127 | Anti-horário | ||||||||||||
MHS | 2,397 | 13 | –1 | |||||||||||||
Posição | 11 | 27 | 18 | |||||||||||||
Orientação | 128 | 221 | 59 | |||||||||||||
Fatores | 6 | 7 | 2 |
Neste caso, onde se estuda uma décima sexta diminuta [3:13] como objeto primal, há oito árvores de tempos na floresta A3 no estado baixo, na sua oitava mutação, conforme ilustra a Figura 11. Tal floresta A3 é uma das treze hierarquias temporais que se podem ex- trair do interior de uma décima sexta diminuta-3:13 no estado baixo.![]()
59
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65

Figura 11: Floresta A3 de árvores de tempos do intervalo 3:13-décima sexta diminuta no estado baixo., 8ª mutação, d0 = 13.
Assim como nas florestas A1 e A2 acima, a coleta de notas na floresta A3 se inicia no nodo raiz da árvore mais à esquerda, isto é, a duração {3}, que é seguida pela raiz da se- gunda árvore {3}, seguida pela raiz da terceira árvore {7}, seguida pela raiz da quarta árvo- re {3}, seguida pela raiz da quinta árvore {3}, seguida pela raiz da sexta árvore {3}, seguida pela raiz da sétima árvore {3} e, então, como último elemento do primeiro nível (ou gera- ção) da floresta, o nodo raiz da oitava árvore {1} é coletado. Considera-se então a segunda geração de durações, de onde, primeiramente, os dois nodos descendentes {2 1} da primei- ra raiz são coletados. Depois, tomam-se os descendentes {2 1} da raiz da segunda árvore, os descendentes {3 3 1} da terceira árvore, os descendentes {2 1} da quarta árvore, os descen- dentes {2 1} da quinta árvore, os descendentes {2 1} da sexta árvore, os descendentes {2 1} da sétima árvore e, para concluir este segundo nível, toma-se o descendente {1} da oitava árvore. Finalmente, a terceira geração produz {1 1 1}, {1 1 1}, {1 1 1 2 1 1}, {1 1 1}, {1 1 1},
{1 1 1}, {1 1 1}, {1 1 1} e {1}.
Quanto à floresta Ω3 mostrada na Figura 12, como em toda floresta do estado alto, há apenas duas árvores de tempos. No caso em estudo, Ω3 é a floresta ômega de uma décima sexta diminuta [3:13] no estado alto, na sua terceira mutação. Tal floresta Ω3 é uma das três hierarquias temporais que se podem criar no interior de tal intervalo no estado alto.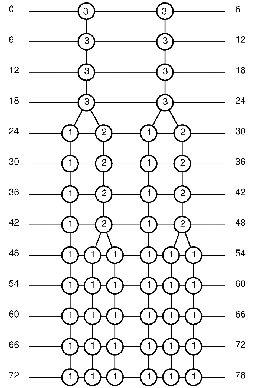
Figura 12: Floresta Ω3 de árvores de tempo de uma décima sexta diminuta (3:13) no estado alto; ritmo da 3ª mutação, d0 = 28.
![]()
60
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
A coleta de notas na floresta Ω3 se inicia no nodo raiz da árvore mais à esquerda, isto é, a duração {3}, que é sucedida pela raiz da segunda árvore {3}. Em seguida, conside- ra-se a segunda geração de durações, de modo que o único nodo descendente {3} da pri- meira raiz é coletado. Toma-se então o descendente {3} da raiz da segunda árvore. A ter- ceira geração produz {3} e {3}. A quarta geração por sua vez também produz {3} e {3}. A quinta geração produz {1 2} e {1 2}. A sexta geração também produz {1 2} e {1 2}. A séti- ma geração também produz {1 2} e {1 2}. A oitava geração também produz {1 2} e {1 2}. A nona geração produz {1 1 1} e {1 1 1}. A décima geração produz {1 1 1} e {1 1 1}. A déci- ma primeira também geração produz {1 1 1} e {1 1 1}. A décima segunda também geração produz {1 1 1} e {1 1 1}. E finalmente a décima terceira segunda também geração produz
{1 1 1} e {1 1 1}.
Assim como no exemplo anterior, por construção, o contraponto C3 é do tipo DD, (ordenação direta × ordenação direta). A partir das sequências de durações extraídas de A3 e Ω3, dois padrões rítmicos R3B e R3A são formados a partir das durações dos respectivos eventos. A Figura 13 mostra a disposição das melodias M3B e M3A calculadas para cada um desses dois padrões rítmicos depois que o objeto intervalar é posicionado no espaço. A es- crita se faz em seis compassos sob uma fórmula de compasso de 4/4, uma vez que a dura- ção total da sequência é de 78 passos de tempo. Em outras palavras, dispondo-se 16 passos (isto é, quatro semínimas) por compasso, todo o contraponto C3 acomoda-se em um total de seis compassos.
Figura 13: Contraponto C3 decifrado no interior de uma décima sexta diminuta (3:13) em equilíbrio. (Áudio on-line disponível em LAMUS 2013a.)
Os três exemplos de contraponto intervalar descritos acima ilustram a essência do método e os resultados musicais que se obtêm quando se manipula o intervalo em equilí- brio. Ainda que os contrapontos estudados C1, C2 e C3 sejam estruturas elementares e, por- tanto, incompletas, do ponto de vista da construção musical, deve-se considerar que eles são tais que poderão vir a crescer segundo modos corretos e consistentes dentro da teoria das árvores de tempos. Primeiramente, deverão crescer verticalmente, para que se arme a estrutura harmônica. Em seguida, deverão crescer horizontalmente, para que se completem as vozes com a justaposição de melodias geradas por objetos intervalares de segunda ordem. Desta maneira, será possível sair-se da condição de comportamento polifônico primitivo do espaço-tempo intervalar para a de uma composição polifônica inteira.![]()
61
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
Abordou-se neste artigo a existência de uma metodologia composicional própria para a criação de contrapontos bem formados, metodologia esta que se fundamenta nos fe- nômenos pertencentes ao interior do intervalo musical, desde que este se encontre no es- tado de equilíbrio. Nestas condições, extraem-se do intervalo duas melodias concorrentes, as quais, em conjunto, apresentam um grau de coesão suficiente para que o encontro entre elas ocorra de maneira significativa e natural no espaço-tempo da música. Os três contra- pontos estudados, embora sejam estruturas musicais pequenas e incompletas, mostram o caminho a ser seguido se o objetivo for a construção de peças polifônicas mais complexas e completas.
No caso das árvores de tempos, a dimensão harmônica se estabelece quando, a cada nota extraída, são extraídas também todas as notas, descendentes dela própria, na hierar- quia da árvore à qual pertence. Desta maneira, todos os níveis da subárvore que tem o nodo (a nota) da vez como raiz iniciar-se-ão acusticamente ao mesmo tempo, gerando-se assim um grupo de notas concomitantes.
A exemplo do contraponto central, a inclusão de outras partes concorrentes, que poderão vir a constituir uma estrutura polifônica bem formada em torno do contraponto in- tervalar primal, também dependerá inteiramente de notas e valores calculados na cinemá- tica do objeto intervalar e na topologia de suas árvores de tempos.
Por fim, assim como o contraponto intervalar segue outros caminhos, que não os definidos pelas regras descritas nos tratados de contraponto – a despeito de ser igualmen- te contraponto, tanto em conceito quanto em resultados – também com relação à harmo- nia que se produzirá pelo ajuntamento ao contraponto central de outras vozes intervalares secundárias, não se utilizam diretamente os preceitos que se encontram nos tratados de harmonia, muito embora haja fundamentação científica notável em algumas obras, sobre- tudo quando se leva em conta a época em que foram escritas, como em J. P. Rameau em
1722 (v. RAMEAU, 1971).
Em composição formal com as árvores de tempos, entretanto, o próprio processo de cálculo das células contrapontísticas cuidará da harmonia intervalar, que deverá indispen- savelmente ser harmonia do mesmo jeito, sempre porque haverá de ser avaliada por ouvin- tes qualificados, como os músicos e os apreciadores da música em geral.
1 O intervalo musical considerado neste artigo é o intervalo justo. Mais precisamente, assume-se o intervalo como sendo um sistema de dois sons senoidais concorrentes, cuja razão de frequências é uma razão de dois inteiros primos entre si, inteiros estes representados por [m:n]. Vale dizer, o único número que se constitui em um fator comum a ambos os inteiros [m] e [n] é a unidade, isto é, mdc (m, n) = 1. Por estão razão, os números [m] e [n] são denominados números harmônicos reduzidos. Além disso, assume-se que m<n, de modo que [m] corresponde ao som baixo, ao passo que [n] corresponde ao som alto. Uma propriedade relevante dos intervalos justos é o fato de terem um período bem definido, isto é, calculável, (v. ARCELA, 2008, Section 2), que é um espaço de tempo representado aqui neste trabalho por τ. A importância do intervalo musical na construção da música está regis- trada em uma infinidade de obras da literatura concernente à teoria da música. Alguns argumentos sobre tal importância podem ser vistos em HINDEMITH, 1968, LEWIN, 1987, ARCELA, 2013.
2 As árvores de tempos são estruturas de dados computáveis – antes de mais nada, são estruturas nativas do mundo interior dos intervalos musicais – as quais são capazes de reunir tempo e espaço numa única peça de informação. Ver ARCELA, 1986, 2000, 2013 (Chapter 5: Forests Alpha and Omega).
3 O objeto intervalar é um modelo formal para o intervalo musical que se baseia na composição ortogonal de mo- vimentos periódicos. (v. ARCELA, 2013, Section 2.4)
![]()
62
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
4 Espaço-tempo intervalar é uma expressão inspirada no conceito de espaço-tempo, que é próprio da teoria da relatividade. O seu emprego neste artigo ocorre não como uma “licença poética” mas sim para valorizar algumas semelhanças que há entre estes dois mundos, o da música intervalar e o da física relativística.
5 Objeto intervalar primal se refere a um tipo de construção melódica inteiramente dentro da significação do conteúdo intervalar enquanto árvores de tempos. A avaliação melódica do objeto primal é de suma importância para que os objetos secundários tenham conteúdo musical consistente.
6 Trata-se da organização hierárquica das árvores de tempos, isto é, diz respeito ao sistema de parentesco, ascen- dência e descendência que há entre os nodos de uma mesma árvore. Há uma harmonia intervalar que pode ser computada em função de tal organização.
7 O objeto intervalar – enquanto primeiro estágio do modelo para o intervalo – é descrito formalmente em ARCE- LA, 2013, (Chapter 2: Modelling Musical Intervals – Section: The Intervallic Object).
8 Quando o intervalo se encontra em equilíbrio, a força da altura ( pitch strength, v. FASTL e STOLL, 1979) é a mesma para ambas as componentes intervalares, isto é, os sons baixo e alto.
9 Grau de coesão é uma expressão adaptada do termo “aderência à tonalidade” usado em SCHOENBERG, 1963, p. 12, §10. Na acepção pretendida neste artigo, indica a afinidade entre as melodias sob contraponto. Poder-
-se-ia dizer numa equação simples: grau de coesão é igual à aderência à tonalidade mais a confluência rítmica entre as duas melodias.
10 Os diversos tipos de caminhamento em árvores são um tópico central na área de estruturas de dados. (v. KNUTH,
1968). O caminhamento por entre os nodos das árvores de tempos usado na extração de padrões rítmicos é um percurso (próprio para árvores) denominado “primeiro em largura”. Em inglês, breadth-first traversal of trees.
11 Evento é o nome dado a cada um dos nodos das árvores de tempos. Cada um deles possui um instante de surgi- mento e um tempo de vida, que corresponde (é proporcional) ao número inteiro existente no próprio nodo. Na sua tradução musical, o evento nada mais é do que uma nota, cujos valores de altura (frequência) e intensidade são calculados na cinemática intervalar.
12 A cinemática intervalar é um tópico discutido conceitual e matematicamente em ARCELA, 2013, Chapter 2: Modelling Musical Intervals, Section 2.4: Intervallic Object. Ver também o Applet 2.4.3: Combined Motion.
13 Para sons puros (senoidais), a força da altura é definida como sendo o produto da amplitude pelo quadrado da frequência (v. ARCELA, 2008). O conceito de força da altura é derivado do conceito de pitch strength que se en- contra em FASTL e STOLL, 1979.
14 As árvores de tempos – enquanto estágio final do modelo para o intervalo – são discutidas algoritmicamente com base em estruturas de dados arborescentes, e em termos de teoria da música quanto ao papel que a partícula intervalar desempenha na construção musical, em ARCELA, 2013, Chapter 5: Forests Alpha and Omega.
15 Também denominada composição algorítmica. Entretanto, pode-se argumentar que se trata de uma qualificação desnecessária, já que, via de regra, toda composição será sempre algorítmica, isto é, a sua construção deverá ter seguido uma sequência de passos formais (metodológicos), seja em uma composição do século XVI (ex. Palestri- na), seja algo escrito no século XX (ex. Schoenberg).
16 A composição de melodias com estruturas formais é um assunto explorado por vários autores, pelo menos des- de os anos 1950, sob diferentes abordagens. Qualquer que seja o modelo empregado – processos estocásticos [XENAKIS, 1957], sistemas baseados em regras [HILLER e BAKER 1964; HILLER, 1969], estruturas linguísticas [LINDBLOM e SUNDBERG, 1969; LASKE, 1973; SUNDBERG e LINDBLOM, 1976; LERDAHL e JAKENDOFF,
1983], ou ainda, como é o caso do presente artigo, árvores de tempos – o objetivo é um sistema musical com o qual seja possível inferir ou calcular melodias.
17 Em intervalos no estado baixo, o número de árvores de tempos da floresta vai desde um mínimo de três – para intervalos menores do que uma oitava – até uma quantidade que depende de quantas oitavas há entre os sons alto e baixo. Há quatro tipos de árvores no estado baixo, quais sejam, primordial, complexa, especular e residual, sendo a árvore especular uma subárvore da árvore complexa. Já no estado alto, a floresta omega contém apenas duas árvores: a esquerda e a telescópica. Em contrapartida, as gerações de cada uma das duas árvores podem se repetir várias vezes (sem ramificação), a depender da largura do intervalo, isto é, de quantas oitavas há entre os sons alto e baixo.
ARCELA, Aluizio. Time trees: the inner organization of intervals. in International Computer Music Conference, Proceedings of the 12th ICMC, Haia. San Francisco, CA: Computer Music Association, 1986, p. 87-89.
. Time trees as virtual worlds. Electronic Musicological Review, 6, 2001. Publicado também nos Anais do VII Simpósio Brasileiro de Computação e Música, Curitiba: Sociedade Brasileira de Computação, 2000.
![]()
63
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
. The computation of pitch with vectors. J. Braz. Comp. Soc., Rio de Janeiro, 14(3):65-85,
2008.
. Melodias em épura. Revista Música em Contexto, Brasília, v.1, Ano 6:85-95, 2012.
. About time trees. Tradução para o inglês da tese de doutorado Arcela, A. “As árvores de tempos e a configuração genética dos intervalos musicais”, PUC-Rio, 1984, com inserções de textos complementares, imagens, áudio, autômatos sônicos e partituras. Publicação web: UnB, Agosto 2013. Disponível em: <http://www.cic.unb.br/docentes/lcmm/att/>. Data do aces- so: 23/10/2013.
. Deciphering rhythms from intervals. (a ser publicado em 2014).
FASTL, Hugo; STOLL, G. Scaling of pitch strength. Hearing Research, 119:293-301, 1979. HILLER, Lejaren. Some compositional techniques involving the use of computers. In: H. Von
Foerster; J. W. Beauchamps (Orgs), Music by computers, p. 71-83, Nova Iorque: Wiley, 1969.
HILLER, Lejaren; BAKER, R. A. Computer cantata: an investigation of compositional procedu- re. Perspectives of New Music 3:62-90, 1964.
HINDEMITH, Paul. The craft of musical composition, Nova Iorque: Schott, v.1, p. 57-64, 1968. KNUTH, Donald E. The art of computer programming, Boston: Addison-Wesley, v.1, p. 315-406,
1968.
KRENEK, Ernst. Studies in counterpoint – based on the twelve-tone technique, Nova Iorque: Schirmer, 1940.
LAMUS, UnB-Website. Contrapontos calculados: Áudio online dos casos aborda- dos neste artigo. Laboratório de Acústica Musical, Universidade de Brasília, 2013(a). Disponível em: <http://www.cic.unb.br/docentes/lcmm/cceti/>. Data do acesso: 10/11/2013.
LAMUS, UnB-Website. Deciphering rhythms: Áudio online dos casos abordados no arti- go “Deciphering rhythms from intervals”, a ser publicado. Laboratório de Acústica Musical, Universidade de Brasília, 2013(b). Disponível em: <http://www.cic.unb.br/docentes/lcmm/ drfi/>. Data do acesso: 10/11/2013.
LASKE, Otto E. In search of a generative grammar for music. Perspectives of New Music,
12(1):351-378, 1973.
LERDAHL, Fred; JAKENDOFF, R. S. A generative theory of tonal music. Cambridge: MIT Press,
1983.
LEWIN, David. Generalized musical intervals and transformations. New Have: Yale University
Press, 1987.
LINDBLOM, Björn; SUNDBERG, J. Towards a generative theory of melody. STL-QPSR, 10(4):
53-86, 1969.
OWEN, Harold. Modal and tonal counterpoint from Josquin to Stravinsky, Nova Iorque: Schirmer,
1992.
RAMEAU, Jean-Philippe. Treatise on harmony, Tradução de Philip Gossett do livro Traité de l’harmonie – Reduite à ses principes naturels (1722). Nova Iorque: Dover, 1971.
SCHOENBERG, Arnold. Preliminary exercises in counterpoint, volume 1. Londres: Faber,
1963.
![]()
64
![]()
ARCELA, A. Um tipo de Contraponto Existente no Espaço-Tempo Intervalar.
Revista Música Hodie, Goiânia, V.14 - n.1, 2014, p. 49-65
XENAKIS, Iannis. A la recherche d’une musique stochastique. Gravesaner Blätter, n.11/12, Ars
Viva Verlag, 1957.
ZARLINO, Gioseffo. The art of counterpoint, Parte 3 de Le Istitutioni Harmoniche (1558). Traduzido por Guy A. Marco e Claude V. Palisca. Nova Iorque: Norton, quarta edição, 1968.
![]()
![]()
![]()
65
![]()