
Revista Música Hodie, Goiânia - V.13, 362p., n.1, 2013
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Resumo: Este artigo apresenta uma série de definições e explanações teóricas que servem de base para uma propos- ta de metodologia analítica para o tonalismo oitocentista, no contexto de uma antecipação de tópicos centrais a um trabalho de pesquisa mais amplo. São apresentadas propostas para uma revisão taxonômica da Teoria da Modulação em dois sistemas de classificação paralelos, segundo os critérios de impacto modulatório e fatura modulatória. O ar- tigo procura demonstrar a fundamentação histórica das proposições analíticas realizadas, destacando em especial, através de alguns exemplos analíticos de repertório, o seu aparelhamento para grafar a linguagem harmônica do to- nalismo expandido do século XIX.
Palavras-chave: Análise musical; Teoria da modulação; Estruturação musical; Harmonia tonal.
The Grounds for a Proposal of an Analytical Methodology for 19th Century Tonality: a taxonomical revision of the theory of modulation
Abstract: This paper presents a series of theoretical definitions and explanations that serve as grounds for the pro- posal of an analytical methodology for 19th century Tonality, in the context of a preview of central topics taken from a larger research work. It presents proposals for a taxonomical review of the Theory of Modulation in two par- allel systems of classification, according to the criteria of modulatory impact and modulatory facture. The paper tries to demonstrate the historical grounds of the analytical propositions made, specially highlighting their ability to graph the harmonic language of 19th century Extended Tonality, by means of a few analytical examples taken from repertoire.
Keywords: Music analysis; Theory of modulation; Music structure; Tonal harmony.
O presente artigo tem como objetivo antecipar ao público acadêmico em geral as bases de uma proposta de metodologia analítica para a música tonal, em especial sua ver- tente cromática da segunda metade do século XIX. Incluem-se nestas bases uma série de proposições de taxonomias, nomenclaturas e simbologias analíticas que estão sendo de- senvolvidas como parte de um projeto de pesquisa de formulação de um modelo estrutural para o tonalismo oitocentista, que visa localizar, explicar e grafar, de uma maneira sintéti- ca, clara e pedagógica, a coerência construtiva dos repertórios da segunda metade do sécu- lo XIX, segundo uma metodologia fundamentada a partir de uma revisão crítica de biblio- grafia teórica histórica da época. Neste processo de pesquisa foi sentida a necessidade de um retorno expressivo a fontes originais oitocentistas, esmiuçando textos musicais do re- pertório de diversas épocas, recompondo e retrabalhando as ideias da natureza dos acordes, da natureza do contraponto, das funcionalidades das harmonias e da lógica dos encadea- mentos harmônicos. Dado o interesse principal da pesquisa no repertório Romântico tar- dio, as fontes mais importantes têm sido, quer de forma direta ou quer mediados por musi- cólogos atuais, textos do século XIX e início do século XX de autores como Gottfried Weber (1779-1839), Anton Reicha (1770-1836), Moritz Hauptmann (1792-1868), François-Joseph Fétis (1784-1871), Arthur von Oettingen (1836-1920), Carl Friedrich Weitzmann (1808-1880), Arnold Schoenberg (1874-1951), Heinrich Schenker (1868-1935) e, em especial, Hugo Riemann (1849-1919). Construída a partir desta revisão crítica de parte do imaginário teórico oitocen- tista, esta pesquisa pretende propor uma maneira alternativa de explicar os procedimentos
Revista Música Hodie, Goiânia - V.13, 362p., n.1, 2013 Recebido em: 15/01/2013 - Aprovado em: 15/04/2013
![]()
135
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
composicionais do Tonalismo Expandido, formalizada em um Modelo Estrutural apresen- tado, na medida do possível, como um sistema lógico dedutivo, “à maneira dos geômetras” como na Ética de Espinoza, da forma mais objetiva e pedagógica possível. Com esta pesqui- sa pretende-se criar não somente um corpo teórico pedagógico para a Estruturação Musical, mas também recuperar para os estudiosos contemporâneos parte do imaginário musical te- órico do século XIX, imprescindível ao entendimento do repertório oitocentista, mas razoa- velmente desconhecido das metodologias tradicionais de instrução musical de hoje.
Grande parte deste trabalho teórico envolve a localização de tratos paradigmáti- cos recorrentes no repertório histórico e a pesquisa e (re)formulação de modelos que pos- sam explicar, classificar e inter-relacionar tais práticas, suas origens, propriedades, desen- volvimentos e transmutações. As tipologias formadas por estes modelos propostos geram um sistema de símbolos e jargões que são utilizados como pontos de acesso semântico ao conteúdo tipológico. Esta simbologia e terminologia tornam-se o grande ferramental básico do processo de formalização e sumarização do entendimento e mapeamento analíticos da Música, configurando o próprio meio de comunicação e repasse pedagógico dos conceitos estudados. É relevante frisar que afinal são estas tipologias de modelos de elementos estru- turais musicais, identificados pelos seus jargões e suas simbologias, vivendo e sobreviven- do através dos tempos em diversas linhagens de trabalhos teóricos, que formam em última instância o próprio imaginário musical dos músicos.
Cabe aqui uma advertência de que existem alguns entraves sérios neste processo de recriação teórica. Um primeiro problema é que os conceitos, teorias e jargões básicos da Teoria da Música não são unificados e muitas vezes são apresentados por diversos teóricos de maneira diferente e por vezes conflitante. Como exemplo, sugiro a leitura da interessan- te comparação realizada por Zamacois (em ZAMACOIS, 1984, p. 235) das ideias sobre pa- rentesco entre tonalidades formuladas por Riemann, Nikolai Rimsky-Korsakov (1844-1908) e Vincent d’Indy (1851-1931). Especificamente a questão das terminologias é bastante pro- blemática, uma vez que um mesmo termo pode não só ter sido definido de maneira diferen- te por diversos autores, como pode ter sido usado para significar coisas absolutamente não-
-relacionadas. A solução para este dilema pede ou a redefinição de certos termos que pelo uso corrente não têm como serem abolidos, assim forçando o teorista a tomar um partido específico em relação a suas escolhas, ou ainda a criação de terminologias absolutamente novas, na esperança de que um jargão diferente não se preste a confusões e mal-entendidos.
Um segundo problema vem da reflexão pertinente de que para a efetividade de um trabalho teórico musical há uma necessidade de uma certa distância temporal entre o ob- servador (o teórico) e o observado (os compositores de uma determinada época e estilo e seu repertório). É apenas com esta distância que se torna possível separar aquilo que é apenas maneirismo isolado de um autor daquilo que é prática comum de uma comunidade de auto- res. O problema é que, com esta distância, o que se ganha em visão perde-se em contato com a prática comum musical viva daquele tempo. Isto porque esta prática não é em sua ínte- gra preservada nos escritos da época: estes comumente tendem a formalizar apenas aquelas questões mais difíceis da linguagem musical do período enquanto questões de entendimen- to mais comum são omitidas pela desnecessidade da expressão de algo de domínio geral (veja o comentário sobre a obra teórica de Tinctoris em JEPPESEN, 1992, p. 9-10, por exem- plo). Sou da opinião de que talvez a melhor atitude para a resolução desta problemática seja aceitar que talvez jamais sejam encontradas todas as peças faltantes deste quebra-cabeças e fixar a atenção no que acontece de recorrente nos próprios textos musicais, explicando-os de maneira relevante às necessidades de nosso próprio tempo, sem no entanto procurar in- ventar novidades teóricas distantes do imaginário de cada época, nem perder contato com![]()
136
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
este imaginário antigo através de um estudo crítico daquilo que foi parcialmente preserva- do nos tratados de época, lembrando-se que estes textos não têm como serem aceitos em sua íntegra sem crítica simplesmente porque também lhes falta uma certa distância temporal do objeto estudado.
Enquanto é preparada a formalização definitiva desta pesquisa em formato de li- vro, alguns de seus aspectos mais importantes estão sendo separados para apresentação à comunidade acadêmica em forma de artigos individuais. Este presente artigo, que retoma um trabalho anterior (BITTENCOURT, 2012) de uma maneira mais precisa, corrigida e con- sideravelmente expandida e revisada, apresenta uma importante parcela deste trabalho re- ferente a uma (re)organização pedagógica de uma Teoria da Modulação – um “reboot”, uma reinicialização, por assim dizer, deste importantíssimo tema da Música –, com reforjamen- tos de definições teóricas e uma taxonomia preparada segundo as preocupações e orienta- ções descritas acima.
Este trabalho está embasado fortemente em uma proposta anterior de nomenclatu- ra e simbologia analítica (ver BITTENCOURT, 2009), desenvolvida para esta pesquisa como ferramental básico para a análise estrutural. Esta taxonomia da modulação somada à refor- ma simbológica aqui mencionada formam o arcabouço básico da proposta de metodologia analítica que instrumentaliza esta pesquisa maior de formulação de um modelo estrutural para o tonalismo oitocentista.
Uma Estrutura Harmônica, de maneira generalizada, é definida nesta proposta teó- rica como uma coleção específica de notas diferentes à qual é atribuído um significado mu- sical que não se altera por meio de rotações (inversões), oitavamentos e embaralhamentos diferentes de suas notas constituintes, e que serve como elemento contextualizador de tudo que harmonicamente e melodicamente ocorre dentro da específica fatia de tempo na qual esta vive. Dentro do contexto do repertório pré século XX, o ideal de estrutura harmônica vem a ser a coleção de notas diferentes que melhor seja capaz de produzir uma alta tonici- dade (a medida da probabilidade de existência de uma fundamental em comum para o es- pectro coletivo das notas soantes – ver BITTENCOURT, 2011 p. 52-53, OETTINGEN, 1866, p. 27-35 e a noção de “tonalness” em PARNCUTT, 1989, p. 25-26 e 58-59) e uma baixa as- pereza (dissonância sensorial causada pelos batimentos relativos à interação das frequên- cias parciais do espectro coletivo das notas soantes – ver PARNCUTT, 1989, p. 25 e 58-59 e HELMHOLTZ, 1875, p. 278). Isto acontece quando se divide um intervalo de diapente (3:2) no ponto de um intervalo de sesquiquarta (5:4), ou seja, isto ocorre com a tríade perfeita maior e sua inversa, a tríade perfeita menor (ver RIEMANN, 1903, pg. 6 e BITTENCOURT, 2011, p. 52-53). Como modelos de perfeição de consonância (uma combinação de alta Tonicidade e baixa Aspereza), as tríades perfeitas têm populado o imaginário musical dos composito- res a séculos e servem de principal elemento contextualizador da simultaneidade de alturas (ver RIEMANN, 1992 p. 87-88). Cabe ainda aqui mencionar que às estruturas harmônicas triádicas da dominante e subdominante podem ser acrescentadas outras notas que, adicio- nando tensão à sua tríade básica, ampliam a definição funcional daquelas estruturas: as sé- timas e nonas na estrutura de dominante e a sexta maior na estrutura de subdominante (ver RIEMANN, 1903, p. 55-61).![]()
137
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
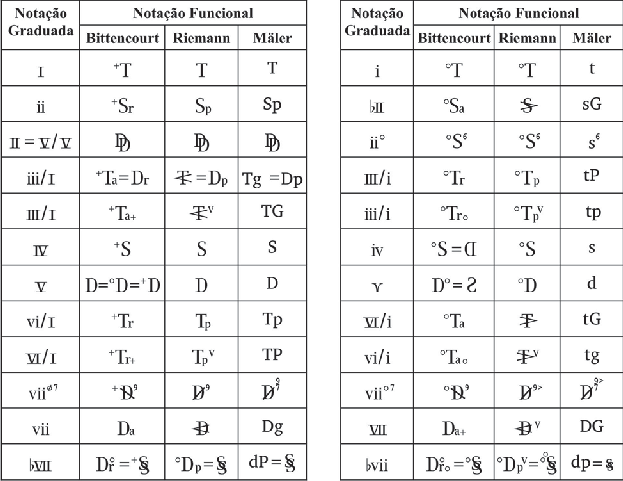
Figura n.1: Tabela de comparação entre simbologias analíticas da Teoria Graduada tradicional e da Teoria Funcional, em três versões diferentes (Bittencourt, Riemann e Mäler).
Nesta proposta de metodologia analítica, as estruturas harmônicas são representa- das segundo a proposta de reforma simbológica da Harmonia Funcional Riemanniana des- crita em BITTENCOURT, 2009, que toma como pontos de partida a nomenclatura original criada por Riemann (ver MICKELSEN, 1977, p. 75-79 e RIEMANN, 1903) e a revisão sim- plificadora realizada por Hermann Grabner (1886-1969) (ver MICKELSEN, 1977, p. 92-94) em sua costumeira tradução ao português (ver KOELLREUTER, 1980 e BRISOLLA, 2006), segundo uma série de requisitos e necessidades específicos traçados pela metodologia ana- lítica aspirada (ver BITTENCOURT 2009, p. 764-765). A Figura 1 mostra uma comparação entre as simbologias da Teoria Graduada tradicional e da Teoria Funcional, tanto na ver- são da reforma simbológica utilizada nesta pesquisa, como ainda comparada às grafias fun- cionais históricas de Riemann e Wilhelm Mäler (1902-1976). As referências utilizadas para esta tabela foram: WEBER, 1851 e GAULDIN, 2004 (notação graduada); BITTENCOURT,
2009 (Bittencourt); RIEMANN, 1903, REHDING, 2003 e MICKELSEN, 1977 (Riemann); LA MOTTE, 1998 (Mäler).
Grandes teóricos musicais como Heinrich Schenker e Hugo Riemann perseguiram a ideia da existência de uma Estrutura Fundamental (uma “Ursatz”, no jargão de Schenker) que serviria como uma ossatura mestra de todo tecido musical. Inspirada pelos modelos![]()
138
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Schenkeriano (a “Urlinie” acoplada ao “Bassbrechung” ou “GrundBassbrechung”, linearmen- te formando um I-V-I; ver KATZ, 1935, p. 314 e PANKHURST, 2008, p. 54) e pelo modelo Riemanniano (sua “große Cadenz”, o I-IV-I em conjunção com I-V-I; ver MOONEY, 2000, p. 84), a presente proposta de modelo de estrutura fundamental baseia-se na notória pro- gressão I-IV-V-I que dá origem aos três modelos cadenciais tradicionais básicos: a cadência completa, a semicadência e a cadência de engano (também chamada de deceptiva, interrom- pida ou evitada). A escolha por utilizar o termo “fórmula” ao invés de “cadência” tem por objetivo eliminar a conotação terminal da palavra cadência, tirando o foco da nossa atenção para além dos instantes de término das frases, visando a noção de um modelo construtivo respeitado por toda progressão harmônica pré século XX.
Assim como em Schenker, que via a tonalidade como uma transformação expan- sional horizontal da tríade perfeita (ver KATZ, 1935, p. 313-315), a presente formalização de um conceito de Estrutura Fundamental representaria também uma trajetória de expansão e contração de um mesmo som inicial (a tônica) mas descrita de uma maneira não exatamente melodicamente linear como em Schenker. O princípio aqui é o de definir a ideia de um lu- gar tonal central (o referido som inicial, a tônica) através de um movimento inicialmente de afastamento deste, seguido de uma refutação deste afastamento com uma condução lógica de retorno ao início. Tradicionalmente a ideia de centro tonal (tese, afirmação) está associa- da com a função harmônica de tônica, a ideia de afastamento desta (antítese, conflito) com a função de subdominante e a ideia de refutação do afastamento e de agente da condução de retorno ao centro (síntese) fica associada com a função de dominante (ver MOONEY, 2000, p. 84-85 e SCHOENBERG, 1995, p. 311).
A presente proposta de ideia de Estrutura Fundamental, claramente Riemanniana (ver REHDING, 2003, p. 47), ficaria então funcionalmente representada por uma sequência T-S-D-T, que efetuaria exatamente este movimento de afastamento de e posterior retorno para um centro arbitrário. Inicialmente, este modelo dá origem às três versões básicas dis- to que aqui é chamado de Fórmula Tonal, uma representando um movimento completo de “aterrissagem” ao centro, outra representando um modelo em que o retorno ao centro fica apenas sugerido mas não completado e ainda outra em que a condução de retorno ao centro é surpreendida por uma “aterrissagem” em um lugar diferente do esperado. E assim fica a formalização esquemática destas versões básicas da fórmula tonal:
- A Fórmula Tonal Completa, que é embasada na cadência completa tradicional: [Tx]-[Sx]-D-T;
- A Fórmula Tonal Incompleta (ou Semi-Fórmula), que é embasada na semicadên- cia tradicional: [Tx]-[Sx]-D;
- A Fórmula Tonal de Engano, que é baseada na cadência de engano (decepti- va) tradicional: [Tx]-[Sx]-D-"surpresa", onde a “surpresa” pode ser implementada com qualquer estrutura harmônica diversa da principal de tônica, com preferên- cia para estruturas que contenham um razoável número de notas de resolução das tensões da dominante.
Nestes esquemas apresentados, os colchetes “[ ]” significam que a área formulaica (ou seja, “relativa à fórmula") é opcional, ou seja, pode ser omitida, e os “x” denotam a pos- sibilidade da área formulaica ser implementada com uma estrutura substituta da harmonia principal em questão, tal como um substituto de sexta (relativo) ou um substituto de sen- sível (antirrelativo) (ver RIEMANN, 1903, p. 71 e p. 80). Note que, de acordo com estas de- finições dadas, não é imprescindível a participação da tríade principal de Tônica em uma fórmula.![]()
139
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Todavia, a fórmula tonal não é uma simples progressão cadencial comum. Ela é um princípio básico, uma ossatura mestra, que pode se alongar no tempo por meio de prolon- gamentos estruturais anexados prefixalmente ou sufixalmente às estruturas harmônicas principais da fórmula e que por meio de prolongamentos melódicos às notas estruturais das estruturas harmônicas, ou seja, por meio das notórias notas estranhas ou não-estrutu- rais, vem a desabrochar na própria superfície de primeiro plano do tecido musical. É desta forma que Riemann pensava um princípio de “Lógica Musical” (ver REHDING, 2003, p. 47). De certo modo, são acopladas aqui as ideias mestras de prolongamento caras a Schenker, adaptadas ao princípio das Funções Harmônicas.
Eventualmente pode-se ainda admitir o uso de estruturas harmônicas substitutas para as áreas formulaicas de dominante das fórmulas completa e incompleta, com destaque para as dominantes extraordinárias e para a regnante. A Regnante é a dominante inversa, uma terminologia dualista de Oettingen (ver OETTINGEN, 1866, p. 67) que é representa- da pela harmonia de iv, sempre como tríade menor. A regnante tem as mesmas proprieda- des funcionais da dominante porém com condução e resolução natural de vozes em sentido invertido. É representada na proposta de simbologia analítica aqui utilizada pelo inverso do símbolo funcional da dominante (ver BITTENCOURT, 2009, p. 766). O uso das versões especulares das letras D e S para denotar a Regnante e a Supra-Regnante (harmonia de v) (OETTINGEN, 1866, p. 67) foi de certo modo inspirado na simbologia de Sigfrid Karg-Elert (1877-1933) (ver MICKELSEN, 1977, p. 90).
Uma Dominante Extraordinária, neste modelo proposto, é uma harmonia substitu- tiva à da dominante principal, construída e efetivamente conectada com a harmonia da tô- nica segundo procedimentos embasados nos esquemas de condução de vozes encontrados nas cadências mais comuns, em especial as cadências de engano tradicionais e o seis-qua- tro cadencial (ver BITTENCOURT, 2009, p. 767-768). A ideia desta coleção de dominantes acessórias, de grande importância para o estudo do repertório da segunda metade do século XIX, inspira-se em sugestões de interconexões pouco ortodoxas entre acordes via modelos básicos de condução de vozes feitas por Karl Friedrich Weitzmann em seu Harmoniesystem de 1860 (ver RUDD, 1992, p. 65-69). Tais conexões mereceram inclusive também a atenção de Schenker (ver os casos de tonicalização em SCHENKER, 1954, p. 265-276). A figura 4 in- clui exemplos do uso de dominantes extraordinárias e regnantes.
A fórmula tonal, neste sentido, representa exatamente este ato de implementação de um centro tonal, um ato necessário de demonstração de um lugar tonal que de certa forma modela, de trás para diante, os “hábitos do ouvido” postulados por Gottfried Weber (WEBER, 1851, p. 345). Com este raciocínio, sem a execução de uma fórmula tonal não pode haver ideia de tonalidade. Assim, coloca-se como proposição que toda estrutura harmônica constante de uma obra musical pré século XX participa inelutavelmente de uma fórmula tonal, estando devidamente inserida nesta e contextualizada por esta.
Nesta presente proposta de metodologia analítica, as fórmulas tonais são represen- tadas delimitando-se sua extensão com uma barra horizontal tendo acima desta os sím- bolos funcionais das estruturas harmônicas agenciadas e tendo abaixo o símbolo da re- gião instanciada pela fórmula (ver Figura 2), segundo a proposta de revisão simbológica da Harmonia Funcional Riemanniana exposta em BITTENCOURT, 2009, e segundo ainda
uma série de convenções adicionais a serem explicadas mais adiante neste artigo.![]()
140
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.

Figura n.2: Exemplo de notação analítica de fórmulas tonais. Fréderic Chopin (1810-1849), Mazurka Op. 7 nº 2 em Lá menor (composta entre 1830-31), compassos 7 a 12.
Bastante trabalhada e desenvolvida por Schoenberg (ver SCHOENBERG, 1969, p. 19-34), a ideia de Região Tonal é definida nesta proposta de modelo de tonalidade como sendo um lugar diatônico tonal (maior ou menor) que é instanciado na percepção do ouvinte por meio da realização de uma fórmula tonal, em uma de suas três versões bá- sicas (ver item anterior). O conceito de região é importante para a compreensão do princí- pio da Monotonalidade (ver SCHOENBERG, 1969, p. 19), segundo o qual uma obra musi- cal se estruturaria sobre uma e somente uma tonalidade, sendo esta tonalidade entendida não como um simples lugar diatônico mas sim como um universo de regiões orientadas hierarquicamente segundo relações de proximidade e distanciamento ao redor de uma região central, que enfim nomeia a tonalidade (ver diagramas em SCHOENBERG, 1969, p. 20 e 30).
O campo harmônico de uma região é definido nesta proposta como sendo a coleção de estruturas harmônicas disponíveis para a confecção de fórmulas tonais naquela região. Ele é formado inicialmente pelas estruturas harmônicas de tônica (I), subdominante (IV) e dominante (V), com ainda o acréscimo de seus respectivos substitutos de sexta e de sen- sível (ver RIEMANN, 1903, p. 71 e p. 80). No modo menor, a presença da dominante, que é sempre uma tríade maior, causa ainda a necessidade de acréscimo ao campo harmônico dos paralelos modais da subdominante (IV ao invés de iv) e da dominante (v ao invés de V), além de seus substitutos de sexta e de sensível, exclusivamente para implementar, respecti- vamente, as passagens diatônicas referentes às versões melódicas ascendente e descendente da escala menor. O conjunto de notas definido e apresentado pelas tríades principais pilares da tonalidade forma o espaço (ou escala) diatônico da região em questão. É interessante su- blinhar aqui que esta ideia de formação das escalas maior e menor a partir das tríades prin- cipais de I, IV e V é bastante antiga e já é mencionada por teóricos como Heinrich Christoph Koch (1749–1816) (ver RUDD, 1992, p. 27-29).
Considerando o conceito de monotonalidade, nesta proposta de metodologia analí- tica uma região é simbolizada através do símbolo funcional que a tríade de tônica desta re- gião teria dentro do campo harmônico da região da âncora tonal central (para o conceito de âncora, ver item 3.1.2.), ainda acrescentando-se um traço horizontal acima do símbolo (ver BITTENCOURT, 2009, p. 768). Este traço horizontal serve para distinguir a nomenclatura
usada para regiões das usadas para estruturas harmônicas (ver Figura 2).![]()
141
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
A Modulação é um dos mais importantes aspectos estruturadores da Música Ocidental e sua importância no estudo da Harmonia e da Estruturação Musical é um fato notório. Em um sentido amplo e geral (e reforça-se aqui a presença da palavra “geral”), a pre- sente proposta define o termo “Modulação” como sendo todo procedimento que agencia a mistura de estruturas harmônicas provenientes de diferentes campos harmônicos. Esta ge- neralização brutal pode ser um tanto inicialmente chocante, mas ela prova-se extremamen- te fecunda pois é a partir dela que a presente taxonomia proposta se desenvolve.
Como cada campo harmônico serve o propósito de agenciar a formação de um cen- tro tonal específico, uma modulação (na definição dada anteriormente) envolve uma certa percepção de deslocamento de centro tonal. A intensidade deste deslocamento de centro to- nal, que chamaremos aqui de Impacto Modulatório, depende da exata maneira como é agen- ciada esta modulação e a medição deste impacto serve como um importantíssimo critério classificativo para as modulações, com significativo impacto para a compreensão analítica estrutural musical. Esta proposta de taxonomia aproveita partes de conceitos já trabalha- dos por diversos teóricos do século XIX (tais como François-Auguste Gevaert (1828-1908) apud ZAMACOIS 1984, 1988, 1990) mas com as terminologias redefinidas, expandidas e/ ou redelimitadas.
Pensando nas diversas maneiras em que uma modulação pode impactar a nos- sa percepção de centro tonal, e ainda considerando o “Principium Inertiae” postulado por Gottfried Weber (ver WEBER, 1851, p. 333-334), existem as seguintes situações nas quais o procedimento de modulação pode, em ordem crescente de impacto modulatório: a) não de- safiar efetivamente a autoridade do centro tonal em vigor; b) efetivar um temporário desvio de foco tonal mas sempre promovendo um periódico retorno a um centro básico recorren- te, que adquire a condição de uma âncora tonal; c) pode efetivar um transporte desta ân- cora tonal para outro local (este é o significado mais tradicionalmente aceito para o termo “modulação”); d) pode destruir a sensação de âncora tonal, promovendo transferências de centro de um ponto imediatamente a outro ponto, sem o recurso da mediação de uma ân- cora tonal recorrente; e e) pode obliterar a sensação de centro, por meio de uma progressão composta exclusivamente por estruturas harmônicas que individualmente formam pratica- mente sozinhas a sua própria fórmula tonal, cada uma apontando para uma região diferen- te. Assim, de acordo com o seu impacto modulatório, as modulações serão classificadas em
5 tipos básicos, a saber: A Tonicização, a Modulação Intratonal, a Modulação Extratonal (ou
Modulação Propriamente Dita), a Travessia e a Errância.
Extremamente trabalhada por diversos teóricos (ver “tonicalização” em SCHENKER
1906, p. 256-261), a Tonicização é definida neste presente modelo como sendo um proce- dimento modulatório no qual uma estrutura harmônica pertencente ao campo harmôni- co da região ativada pela fórmula tonal é prolongada prefixalmente por meio de uma outra estrutura harmônica emprestada do campo harmônico que tem como tônica a própria es-![]()
142
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
trutura a ser prolongada. Aqui a mistura de elementos de diversos campos harmônicos é suave o suficiente para que não ocorra um real deslocamento do centro tonal estabelecido pela fórmula. Mais comumente, este tipo de modulação envolve o uso de dominantes in- dividuais, também tradicionalmente ditas “secundárias” (ver BRISOLLA 2006, p. 63), um tipo de prolongamento estrutural prefixal que introduz uma estrutura harmônica por meio de sua própria dominante, ou seja, por meio da dominante constante do campo harmônico no qual o elemento “tonicizado” (ou seja, a estrutura a ser prolongada prefixalmente) é tô- nica. Sublinha-se aqui o fato de que a estrutura tonicizada não perde a função harmônica que esta exerce na fórmula tonal ativadora da região original, e é precisamente por isso que pode-se dizer que a tonicização é um procedimento de impacto modulatório zero, pois não vence o “Principium Inertiae” (WEBER, 1851, p. 333-334).
Na presente proposta de metodologia analítica, a tonicização é indicada usando-se o símbolo da região do campo harmônico emprestado colocado entre parênteses abaixo da notação analítica funcional da estrutura harmônica tonicizadora, de acordo a proposta de simbologia descrita em BITTENCOURT 2009, p. 768 (ver Figura 3). Como todo símbolo en- tre parênteses sempre se refere a uma região, é desnecessário o uso do traço horizontal aci- ma do símbolo.
Figura n.3: Exemplo de notação analítica de tonicizações. Fréderic Chopin, Mazurka Op. 7 nº 2 em Lá menor, compassos
13 a 16.
A Modulação Intratonal é definida neste presente modelo como um procedimento modulatório em que são alternadas fórmulas tonais em regiões vizinhas de maneira a que seja obtida uma percepção da existência de uma região central básica e recorrente, uma Âncora Tonal, que se impõe como centro efetivo.
Aqui a modulação tem impacto suficiente para deslocar o centro tonal para uma região vizinha mas apenas de maneira temporária, de onde logo volta-se à região ânco- ra. Este é o modo de proceder mais característico de um tecido musical tonal tradicional, configurando-se no modelo básico de estabilidade tonal. É como se as outras tonalidades vizinhas servissem de “postos avançados” da tonalidade central, estendendo e ajudando a delimitar as fronteiras desta através da proposição de contrastes diatônicos. É aqui que é construída a noção de uma Grande-Tonalidade (uma “Tonalidade com T maiúsculo”), um universo de tonalidades em que estas são organizadas hierarquicamente ao redor de uma única tonalidade principal segundo relações de proximidade e distância. Enfim, é o mesmo espírito do princípio da Monotonalidade descrito por Schoenberg (SCHOENBERG
1969, p. 19-20).![]()
143
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Este termo “modulação intratonal” já foi anteriormente trabalhado por Gevaert (ver ZAMACOIS 1988, p. 133-134), mas referindo-se, dado os exemplos musicais dados por Zamacois, ao contexto daquilo que neste presente modelo está definido como tonicização. O conceito de “intratonal” aqui exposto mantém a ideia de Gevaert de uma ação que pro- voca momentânea e passageira transferência de centro tonal, mas agora considerando o elemento contextualizador da “monotonalidade” Schoenbergiana. Em outras palavras, esta transferência de centro é momentânea porque existe uma clara preocupação contextual de manutenção de uma Âncora Tonal, e é precisamente isso que faz com que “toda digressão seja considerada como sendo ainda dentro da mesma tonalidade, quer diretamente ou indi- retamente, proximamente ou remotamente relacionada” (SCHOENBERG 1969, p. 19).
Na presente proposta de metodologia analítica, a modulação intratonal é indicada pela marcação de região incluída abaixo da barra horizontal delimitadora da fórmula tonal, sendo que o símbolo funcional utilizado deve especificamente revelar a relação de paren- tesco que a região da fórmula analisada possui com a âncora tonal do trecho musical em questão (ver Figura 2). Caso a âncora tonal da passagem em questão seja diferente da tonali- dade principal da obra, deverá ser ainda acrescentado, entre parênteses e abaixo da notação básica da região, outra nomenclatura contendo o símbolo funcional que especificamente re- vele a relação de parentesco mantida entre a âncora tonal do trecho em questão e a tonali- dade principal da obra. Na Figura 4, por exemplo, que mostra o início do segundo tema do primeiro movimento da Nona Sinfonia de Anton Bruckner (1824-1896) em Ré Menor, as re- giões das fórmulas em Lá Maior, Mi Maior, Lá Menor, Sol Maior e Fá sustenido Maior são identificadas em relação a Lá Maior, que é a âncora tonal da passagem em questão. As nota- ções em parênteses abaixo da notação de região revelam a relação que a âncora (Lá Maior) possui com a tonalidade principal do movimento (Ré Menor).
![]()
144
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.

Figura n.4: Exemplo de notação analítica de modulações intratonais e extratonais. Anton Bruckner (1824-1896), Nona
Sinfonia, em Ré menor (1887-96), primeiro movimento, compassos 97-108.
A Modulação Extratonal refere-se neste modelo ao procedimento de transporte do eixo central de modulação intratonal (a âncora tonal) para outro ponto. Seria aqui pos- sível ter chamado este tipo de “Modulação Propriamente Dita”, considerando-se que este termo denota aquilo que teóricos como Schoenberg comumente entendem pela palavra “modulação”:
Não se deve falar de modulação a menos que uma tonalidade tenha sido definitiva- mente abandonada, e por um tempo considerável, e outra tonalidade tenha se estabe- lecido quer harmônica quer tematicamente. (Schoenberg, 2004, p. 37)
Aqui o impacto da modulação é capaz de deslocar a âncora tonal para outra loca- lidade, ao redor da qual serão desenvolvidas novas sessões de modulação intratonal. Este é mais um termo que revisita ideias de Gevaert (ver ZAMACOIS 1984, p. 194), mas com sig- nificado reforjado e ampliado.
Na presente proposta de metodologia analítica, a modulação extratonal é grafada a partir da própria notação de região relativa à modulação intratonal, sendo indicada exata- mente por aquele símbolo funcional incluído entre parênteses abaixo da notação básica da região, conforme explicado no item anterior. O exemplo da Figura 4 indica que houve uma modulação extratonal, uma vez que a âncora tonal do tema em questão é diferente da tona- lidade principal do movimento (Ré Menor).
Esta nomenclatura analítica permite distinguir situações onde uma mesma tonali- dade representaria, em diferentes seções de uma obra, relacionamentos regionais diferentes conforme a âncora tonal de cada contexto. Por exemplo, em um trecho musical ancorado em Dó Maior, Lá Menor representaria a região de tônica relativa desta âncora, mas se a âncora migrar para Sol Maior o mesmo Lá Menor passa então a representar a região de subdomi- nante relativa da região principal. Na minha opinião, é muito importante para a compreen- são estrutural da Música que estas distinções sejam iluminadas e grafadas claramente pela
simbologia analítica.![]()
145
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
A palavra Travessia aqui utilizada é inspirada no notório termo musical alemão “Durchführung” (ver GROVE, 1879, p. 472), a este propondo uma versão portuguesa. Neste modelo, a Travessia denota um procedimento no qual fórmulas em regiões diferentes se su- cedem sem a preocupação de manutenção de uma âncora tonal, ou seja, com a passagem entre as regiões ocorrendo de um ponto a outro ponto de maneira que, a princípio, seja sig- nificativo apenas o relacionamento entre a nova região e a última ouvida. A travessia repre- senta o modelo básico de instabilidade tonal e é utilizada tradicionalmente sobretudo na construção de Desenvolvimentos e Transições.
Na presente proposta de metodologia analítica, a travessia é grafada colocando-se abaixo da barra horizontal delimitadora da fórmula não uma mas duas nomenclaturas para a região, separadas por um sinal de igualdade diatônica (homógrafa) ou enharmônica (ver BITTENCOURT, 2009, p. 769). A primeira notação, à esquerda, indica em dois níveis (ou seja, um símbolo simples e um entre parênteses imediatamente abaixo) o relacionamento que a nova região entretém com a última região ouvida, colocando-se o símbolo deste rela- cionamento acima do símbolo da região anterior, este último entre parênteses. A segunda notação, à direita, indica em um nível apenas (ou seja, sem notações entre parênteses) a re- lação que a nova região mantém com a tonalidade principal da obra. Este método serve dois propósitos: 1) a primeira notação revela o que tem de significativo no passo de modulação por travessia, ou seja, a relação de ponto a ponto; e 2) a segunda notação serve para identifi- car em um nível apenas esta região em uma fórmula futura, assim evitando a inconveniên- cia da próxima notação de relacionamento ponto a ponto terminar com três ou mais níveis. Isto é viável porque com a proposta de simbologia funcional aqui adotada é sempre possí- vel descrever com apenas um único nível qualquer relacionamento entre duas regiões (ver Figura 5 e BITTENCOURT 2009, p. 768).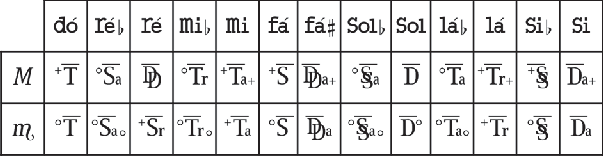
Figura n.5: Tabela de relações entre a tonalidade de Dó Maior e todas as outras demais regiões, medidas da maneira mais direta possível (retirada de BITTENCOURT, 2009, p. 769).
A Figura 6 exemplifica o processo de análise de um trecho de travessia. Neste exemplo, a nomenclatura analítica procura revelar e grafar em símbolos a repetição sequen- ciada da mesma operação modulatória, de ponto a ponto sempre à região da Tro da última ouvida, percorrendo assim um ciclo ascendente de terças menores (ou seja, via relações mediânticas).![]()
146
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.

Figura n.6: Exemplo de notação analítica de uma travessia. Franz Schubert (1797-1828), Sonata para piano em Lá Menor
D. 845 Op. 42 (1825), primeiro movimento, compassos 165-177.
Na presente proposta, a Errância é definida como um procedimento radical no qual a sensação de centro tonal é obliterada por meio de uma progressão composta principalmen- te por estruturas harmônicas de dominante, cada uma apontando para uma região diferente ou ainda para várias regiões diferentes, no caso do uso de dominantes de estrutura simétri- ca enharmonizável (ver “vagrant harmony” em SCHOENBERG, 1969, p. 44). De certo modo, a obliteração do centro se dá pela mudança rápida e pelo excesso e multiplicidade de indi- cações de centro. Em suma, esta ideia é basicamente análoga ao conceito de “harmonia er- rante” desenvolvido por Schoenberg (ver “roving harmony” em SCHOENBERG, 1969, p. 3). Funcionalmente, cada dominante da passagem forma sozinha a sua própria semi-fórmula to- nal e de certa forma é por isso que, neste caso, a sequência de acordes não “(...) consegue ex- pressar inequivocamente uma região ou tonalidade” (SCHOENBERG, 1969, p. 3). No entanto, o resultado final disto é que juntas as estruturas harmônicas terminam por formar um gran- de prolongamento de uma área formulaica de dominante, à maneira de uma sequência de dominantes extraordinárias, apenas aguardando que uma das dominantes culmine em seu alvo tônico esperado, desta forma estancando o processo de errância. Este procedimento é geralmente de curta duração e aparece geralmente como uma intensificação radical dos mo- vimentos modulatórios de uma travessia, em especial dentro de seções de Desenvolvimento. Seu final é geralmente e naturalmente uma semicadência que reconquista, senão uma ân- cora tonal, ao menos um centro provisório iniciador de novos procedimentos de travessia.
A errância geralmente envolve a conexão de diversas dominantes via Transformação Cromática, ou Parentesco Transformacional (ver BITTENCOURT, 2009, p. 769). Duas har- monias possuem parentesco transformacional se alguma variante da primeira harmonia (com nona, com quinta cromatizada, com omissões de fundamental, etc.) for idêntica a al- guma variante da segunda, quer de maneira diatônica (homógrafa) ou enharmônica (ver![]()
147
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
BITTENCOURT, 2009, p. 769). Este procedimento é capaz de transformar facilmente uma dominante em outra por meio de uma combinação de movimentos cromáticos e diatônicos parcimoniosos, o que parece ser certamente uma evolução da lei do “caminho mais curto” apregoada por Bruckner (ver SCHOENBERG, 2001, p. 84). Este tipo de relacionamento (indi- cado na proposta de simbologia aqui adotada pelo sinal ≈) é encontrado especialmente entre a dominante principal e as dominantes dos substitutos diatônicos diretos ou emprestados re- lativos e antirrelativos da tônica. Isto leva a crer que tais encadeamentos foram “aprendidos”, por assim dizer, a partir das conexões entre dominantes praticadas tradicionalmente em fór- mulas tonais de engano envolvendo tonicização do elemento harmônico surpresa, como por exemplo as sequências [V7 – V7/vi – vi], [V7 – V7/iii – iii] e suas demais variantes modais diretas ou emprestadas. Tais tipos de conexão entre acordes dissonantes, tornados possíveis pelo uso criativo da manutenção parcial de paradigmas básicos naturais de condução de vo- zes, já eram de alguma maneira tentativamente mapeados por teóricos do século XIX como Weitzmann (ver “deceptive progression” em RUDD, 1992, p. 65-66) e Reicha (ver “resoluções excepcionais de dissonâncias” em REICHA, 1890, p. 154 e REICHA, 1830, p. 2-5).
Na presente proposta de metodologia analítica, a errância é grafada usando-se os mesmos princípios utilizados nas marcações de travessia, mas com a barra horizontal deli- mitando não mais exatamente as fronteiras das fórmulas tonais mas sim áreas de contextu- alização tonal para as estruturas harmônicas grafadas. Assim, dependendo do que melhor convier para o trecho musical específico analisado, as estruturas harmônicas serão contex- tualizadas: a) na última região formada antes do processo errante ou na região finalmente conquistada ao término da errância, com as dominantes contraditórias marcadas como se fossem tonicizações sem alvos ou ainda como dominantes extraordinárias; ou b) em diver- sos pequenos estágios formulaicos à medida que seja possível decodificar e grafar a origi- nação paradigmática típica dos encadeamentos efetuados entre as dominantes; ou ainda c) em uma combinação de todos os princípios acima. O que se deve ter em mente é que grafar exatamente quais são os múltiplos centros apontados pelas dominantes não é de muita im- portância e raramente é pertinente. O importante é grafar a maneira e a razão com a quais as dominantes se convertem umas nas outras, mapeando este ato de prolongamento de uma tensão de instabilidade tonal até a reconquista de um novo centro. O exemplo da Figura 7 mostra um exemplo de errância onde é possível observar claramente estas conexões via pa- rentesco transformacional cromático, notando-se em especial as dominantes conectadas segundo a condução de vozes das cadências de engano tonicizadas típicas [V7 – V7/vi – vi] (compassos 137-138 e 141-142) e [V7 – V7/iii – iii] (compassos 143-144).
Figura n.7: Exemplo de notação analítica de uma errância. Schubert, Sonata para piano em Lá Menor D. 845 Op. 42, primeiro movimento, compassos 137-144.
![]()
148
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Este projeto de taxonomia da modulação completa-se com a identificação da Fatura Modulatória. Aqui o critério de classificação é a maneira como é gerenciada a área de fron- teira entre as duas fórmulas tonais envolvidas, ou seja, a maneira como é evidenciada e construída − daí o termo “fatura” − a mistura e introdução dos elementos de diferentes campos harmônicos. Este critério da Fatura é sempre observável em todos os tipos de mo- dulação segundo o impacto modulatório vistos anteriormente.
Uma primeira estratégia básica para efetuar a conexão entre regiões é a utilização de um elemento mediador − chamado tradicionalmente de “pivô” − que é compartilhado pelos dois campos harmônicos envolvidos. Estrategicamente posicionado na área de fron- teira entre as duas fórmulas tonais, este elemento mediador é uma estrutura harmônica que opera simultaneamente e corretamente − ou seja, participa bona fide do desenrolar das fór- mulas tonais em que se inclui − tanto como término da última fórmula ouvida como iní- cio da próxima fórmula (nos casos de tonicização, considera-se o par tonização-tonicizado como uma “micro-fórmula”). Tal estratégia de interconexão entre regiões diferentes, reali- zada por meio de um elemento harmônico que sofre, por assim dizer, uma re-significação funcional, era compreendida e descrita em detalhes já no começo do século XIX. Por exem- plo, Gottfried Weber explica que “a mesma espécie de harmonia fundamental pode ocor- rer em diversos graus de uma escala, e efetivamente pode pertencer a uma tonalidade em um contexto e a outra, em outro contexto” (WEBER, 1851, p. 289), o que desenvolve o con- ceito de “Mehrdeutigkeit” (múltiplo significado), de Georg Joseph Vogler (1749-1814) (ver DAMSCHRODER, 2008, p. 155-156). Criada por Vogler e Weber (ver BERNSTEIN, 2002, p. 778-788), a técnica analítica da Harmonia Graduada procura demonstrar e evidenciar exatamente esta questão.
Uma estrutura harmônica pivô será, nesta proposta, considerada de tipo “direto” quando esta existir em ambos os campos harmônicos simples envolvidos. Entende-se nes- te modelo por campo harmônico simples o conjunto das estruturas harmônicas básicas de uma tonalidade (os pilares T, S e D, incluindo-se, quando em modo menor, também as va- riantes modais +S e D° de uso melódico mencionados no item 2.3.), mais os seus substitutos de sexta (relativos) e de sensível (antirrelativos).
Neste modelo, se a estrutura pivô existir nomeada com soletramento idêntico nos dois campos harmônicos simples envolvidos ele será um Pivô Direto Homógrafo, ou mais simplesmente, um Pivô Diatônico. Uma modulação efetuada com este tipo de pivô é a mes- ma conhecida tradicionalmente como “modulação diatônica” (ver ZAMACOIS, 1984, p. 202 ou BRISOLLA, 2006, p. 77). O truque aqui é que caminha-se de maneira diatônica em uma região até o elemento mediador e deixa-se este também diatonicamente, mas agora na nova região. Em outras palavras, este procedimento impede o choque direto entre os elementos conflitantes dos espaços diatônicos das duas regiões envolvidas. Esta dupla função da es- trutura harmônica pivô deve ser identificada nas análises por meio de duas marcações fun-![]()
149
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
cionais para a estrutura harmônica pivô, separadas pelo sinal de igualdade diatônica (=) (ver BITTENCOURT, 2009, p. 769). A Figura 8, entre os compassos 109 e 110, exemplifica esta ideia, grafando analiticamente o papel de pivô diatônico (ou pivô direto homógrafo) que a tríade de Ré menor desempenha na área de fronteira entre as fórmulas em Ré menor e Mi bemol Maior.
Figura n.8: Exemplo de notação analítica de uma Modulação Pivotada com Pivô Diatônico e de uma Modulação Não- Pivotada via um processo de transformação cromática. Schubert, Sonata para piano em Lá Menor D. 845 Op. 42, primeiro movimento, compassos 109-114.
Também são incluídos exemplos de pivôs diatônicos na Figura 6 (compassos 168,
176 e também o 172, desconsiderando-se a enharmonia entre as regiões de Sol bemol menor e Fá sustenido menor). Ressalva-se aqui que em casos de tonicização é um tanto supérfluo e irrelevante assinalar pivôs nas marcações analíticas, pois não há uma real proposta de mu- dança de região, algo que desafie ou rompa o entendimento da fórmula tonal. Tal marcação apenas obscureceria o fato analítico que se quer grafar (a própria tonicização).
É possível também efetuar o mesmo raciocínio acima usando como pivô uma estru- tura harmônica que exista nomeada com soletramento diferente nos dois campos harmôni- cos simples envolvidos. Neste caso, este será um Pivô Direto Enharmônico. Uma modulação efetuada com este tipo de pivô é basicamente a mesma conhecida tradicionalmente como “modulação enharmônica” (ver ZAMACOIS, 1990, p. 55 ou BRISOLLA, 2006, p. 80). A du- pla função do pivô direto enharmônico deve ser identificada nas análises por meio do sinal de igualdade enharmônica (@) (ver BITTENCOURT, 2009, p. 769). A Figura 9 dá um exem- plo de pivô direto enharmônico (compasso 23) que faz uso da notória equivalência enhar- mônica entre tétrades de sétima diminuta a uma terça menor de distância, propondo um “atalho” que quebra e encurta uma sequência de dominantes em ciclo de quintas.
Figura n.9: Exemplo de notação analítica de um Pivô Direto Enharmônico. Fréderic Chopin (1810-1849), Mazurka Op. 7 nº 2 em Lá menor, compassos 22 a 25.
![]()
150
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Neste modelo, uma estrutura harmônica pivô será de tipo “emprestado” quando esta existir nos dois campos harmônicos envolvidos apenas se considerarmos as versões expan- didas destes campos por acréscimos via processos de empréstimo modal (algo esboçado, por exemplo, com as “relações com a subdominante menor” em SCHOENBERG, 2001, p. 323). Neste processo de expansão, é agregado ao campo harmônico simples de uma região novas estruturas harmônicas obtidas por meio de combinações de operações de inversão de pola- ridade modal (maior para menor ou vice-versa), de substituição de sexta e de substituição de sensível, em diversos ordenamentos diferentes, realizadas a partir das estruturas harmô- nicas básicas pilares da tonalidade (T, S e D, incluindo-se as variantes modais do modo me- nor mencionadas no item 2.3.). Tais combinações de operações, que já eram parcialmente mapeadas por Riemann no século XIX (ver RIEMANN, 1903, p. 88-106), terminam por con- textualizar e incluir em um mesmo campo harmônico todas as 12 tríades perfeitas maiores e todas as 12 tríades perfeitas menores, de maneira hierarquizada segundo relações decres- centes de proximidade, de acordo com a quantidade de operações envolvidas: quanto maior for o número destas para se chegar à nova estrutura harmônica a partir de uma das tríades básicas pilares da tonalidade, mais distante hierarquicamente será o resultado.
Seguindo este raciocínio, o campo harmônico expandido de uma região será for- mado por quatro órbitas de relacionamento em ordem decrescente de proximidade hierár- quica. Na primeira órbita circulam os próprios pilares básicos e as estruturas harmônicas resultantes da sujeição destes a apenas uma operação de substituição de sexta ou de sensí- vel − ou seja, aqui circula o próprio campo harmônico simples da região; na segunda órbi- ta circulam as estruturas resultantes da sujeição dos pilares a uma operação de inversão de polaridade modal, seguida opcionalmente por uma operação adicional de substituição de sexta ou de sensível − em outras palavras, circula aqui todo o campo harmônico simples da região paralela modal; na terceira órbita circulam estruturas resultantes da sujeição dos pilares a uma operação de substituição de sexta ou de sensível seguida de uma operação de inversão de polaridade modal; na quarta órbita circulam estruturas resultantes da sujeição dos pilares a uma sequência de três operações, nesta ordem: uma de inversão de polaridade modal, uma de substituição de sexta ou de sensível e uma de inversão de polaridade modal
− ou seja, é aplicado nos elementos da segunda órbita o princípio que gerou a terceira órbita.
Em relação ao processo de fatura de uma modulação pivotada, este procedimen- to implicará em uma situação em que sempre é possível encontrar estruturas pivôs entre quaisquer duas tonalidades, por mais esdrúxulos e distantes que possam parecer os rela- cionamentos tonais propostos. Isto termina por fornecer subsídios para a compreensão da afirmação de Weitzmann de que “entre duas tríades consonantes conectadas por meio de uma condução natural de vozes sempre é possível demonstrar uma conexão interna ou re- lacionamento” (HARRISON, 1994, notas da p. 1). É evidente aqui que a consequência deste raciocínio é a formação do próprio conceito oitocentista de Tonalidade Expandida.
Neste modelo, analogamente aos pivôs de tipo direto, se a estrutura pivô empresta- da existir nomeada com soletramento idêntico nos dois campos harmônicos envolvidos ape- nas considerando-se as suas versões expandidas, ela será um Pivô Emprestado Homógrafo. Se o pivô existir nomeado com soletramento diferente nos dois campos harmônicos envol- vidos apenas considerando-se as suas versões expandidas, ele será um Pivô Emprestado Enharmônico. A dupla função destes pivôs deve também ser identificada nas análises por meio dos sinais de igualdade diatônica (=), para casos de homografia, e de igualdade enhar- mônica (@), para os de enharmonia. A Figura 10 exemplifica um pivô emprestado homógrafo
de segunda órbita, conectando duas tonalidades menores em relação mediântica (Lá menor e![]()
151
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Dó menor) através de um elemento do campo harmônico de Dó maior, ou seja, através de um membro da segunda órbita de relacionamentos do campo harmônico expandido de Dó menor. Também é incluído um exemplo de pivô emprestado homógrafo na Figura 2 (compasso 8).
Figura n.10: Exemplo de notação analítica de um Pivô Emprestado Homógrafo de segunda órbita. Fréderic Chopin (1810-
1849), Mazurka Op. 7 nº 2 em Lá menor, compassos 15 a 18.
Uma segunda estratégia para efetuar a conexão entre regiões é a utilização de um processo de transformação que converte a última estrutura harmônica da primeira fórmula na primeira estrutura da fórmula seguinte por meio de um procedimento de Transformação Cromática (ver item 3.1.5.), ou seja, através de uma combinação de movimentos de condução de voz cromáticos e diatônicos parcimoniosos. Enquanto a estratégia utilizada pela fatura modulatória pivotada é a de buscar impedir, pelo uso de uma estrutura harmônica comum, o choque direto entre os elementos conflitantes dos espaços diatônicos diferentes envolvi- dos, na modulação de fatura não-pivotada é valorizado precisamente o evidenciamento des- te choque por meio de um processo de “distorção melódica”, que introduz ao mesmo tempo um conflito − na forma de um contraste diatônico à primeira região ouvida − e uma im- pulsão inequívoca em direção à concretização do desvio para outro campo harmônico. Esta ideia é basicamente análoga à conhecida tradicionalmente como “modulação cromática” (ver ZAMACOIS, 1984, p. 208 ou BRISOLLA, 2006, p. 80).
A ocorrência deste método de junção entre regiões pode ser identificada nas análises por meio do sinal de Parentesco Transformacional (≈), inserido entre as duas estruturas har- mônicas que formam a área de fronteira entre as fórmulas envolvidas (ver BITTENCOURT,
2009, p. 769). A Figura 8, entre os compassos 113 e 114, exemplifica esta ideia de modulação de fatura não-pivotada, grafando analiticamente a conversão da tríade de Mi bemol maior (Tônica na primeira fórmula) na tríade de Dó maior (Dominante na segunda fórmula), por meio de um processo de transformação cromática. Ressalva-se aqui novamente, e pelas mes- ma razões, que geralmente é irrelevante a marcação analítica deste relacionamento em ca- sos de tonicização. No entanto, às vezes pode ser pertinente tal marcação como na situação de Errância mostrada na Figura 7.
Atualmente em processo de formalização em um tratado de escopo e fôlego maio- res ainda em preparação, este ferramental analítico e os conceitos teóricos aqui apresenta- dos têm demonstrado considerável utilidade pedagógica em aulas de Harmonia e Análise![]()
152
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
Musical, praticados sempre de forma comparada e contraposta aos ferramentais clássi- cos da Harmonia Graduada e da Harmonia Funcional tradicional. Este trabalho pedagó- gico tem servido de campo de testes para o desenvolvimento desta proposta de metodolo- gia analítica, e está sempre mostrando − ou mesmo forçando − novos caminhos a seguir, apontando falhas e miopias a serem corrigidas, isto à medida com que se verifica a efici- ência (ou não) da ação de decupagem estrutural deste modelo teórico proposto nas obras do repertório oitocentista. É natural então que estas proposições venham a sofrer subse- quentes modificações e ajustes em um futuro próximo. Neste artigo, tentou-se demonstrar a fundamentação histórica da presente proposta de Taxonomia da Modulação, destacando-
-se em especial o seu aparelhamento para grafar a linguagem harmônica do tonalismo ex- pandido do século XIX.
1 Esse artigo é uma versão revisada e expandida de artigo previamente publicado em anais de congresso.
BERNSTEIN, David W. Nineteenth-century harmonic theory: the Austro-German legacy. In: CHRISTENSEN, Thomas (ed.). The Cambridge History of Western Music Theory. Cambridge: Cambridge University Press, 2002. Capítulo 25.
BITTENCOURT, Marcus Alessi. Apresentação de uma reforma simbológica para a análise harmônica funcional do repertório tonal. In: Anais do XIX Congresso da ANPPOM. Curitiba: ANPPOM, 2009.
. Sketches for the foundations of a contemporary experimental treatise on Harmony. In: Anais do II Encontro Internacional de Teoria e Análise Musical. São Paulo: UNESP-USP- UNICAMP, 2011.
. Um “Reboot” para a Teoria da Modulação, com o Impacto Modulatório como critério de classificação. In: Anais do IV Encontro de Musicologia de Ribeirão Preto. Ribeirão Preto-SP: Universidade de São Paulo, 2012.
BRISOLLA, Cyro. Princípios de harmonia funcional. São Paulo: Annablume, 2006. DAMSCHRODER, David. Thinking about Harmony: Historical Perspectives on Analysis. New
York: Cambridge University Press, 2008.
GAULDIN, Robert. Harmonic Practice in Tonal Music. New York: W.W. Norton & co., 2004. GROVE, George (ed.). A Dictionary of Music and Musicians, Vol. 1. London: Macmillan and Co., 1879. HELMHOLTZ, H. On The Sensations of Tone as a Physiological Basis for the Theory of Music.
London: Longmans, Green, and Co. 1875.
JEPPESEN, K. Counterpoint: the polyphonic vocal style of the sixteenth century. New York: Dover Publications, 1992.
KATZ, Adele T.. Heinrich Schenker’s Method of Analysis. The Musical Quarterly, Oxford
University Press, Vol. 21, No. 3, p. 311-329, 1935.
KOELLREUTER, Hans Joachim. Harmonia Funcional – introdução à teoria das funções harmô- nicas. São Paulo: Ricordi Brasileira, 1980.
![]()
153
![]()
BITTENCOURT, M. A. O Arcabouço de uma Proposta de Metodologia Analítica para o Tonalismo do Século XIX: uma revisão taxonômica da teoria...
Revista Música Hodie, Goiânia, V.13 - n.1, 2013, p. 135-154.
HARRISON, Daniel. Harmonic Function in Chromatic Music: a renewed dualist theory and an account of its precedents. Chicago: University of Chicago Press, 1994.
LA MOTTE, Diether de. Armonía. Barcelona: Idea Books, 1998.
MICKELSEN, William C. Hugo Riemann’s Theory of Harmony: a study. Lincoln: University of
Nebraska Press, 1977.
MOONEY, Kevin. Hugo Riemann’s Debut as a Music Theorist. Journal of Music Theory, Duke
University Press, Vol. 44, No. 1, p. 81-99, 2000.
OETTINGEN, Arthur von. Harmoniesystem in Dualer Entwicklung. Leipzig: W. Glaser, 1866. PANKHURST, Tom. SchenkerGUIDE: a brief handbook and website for Schenkerian analysis.
New York: Routledge, 2008.
PARNCUTT, Richard. Harmony: a psychoacoustical approach. Berlin: Springer-Verlag, 1989. REHDING, Alexander. Hugo Riemann and the birth of modern musical thought. Cambridge:
Cambridge University Press, 2003.
REICHA, Anton. Corso di Composizione Musicale. Milão: G. Ricordi & C., 1890.
. A New Theory of the Resolution of Discords according to the Modern System. London: R. Cocks & Co., 1830.
RIEMANN, Hugo. Harmony Simplified; or, The theory of the tonal functions of chords. London: Augener & Co., 1903.
. Ideas for a Study “On the Imagination of Tone”. Journal of Music Theory, Vol. 36, No. 1 (Spring), p. 81-117, 1992.
RUDD, Rachel Eloise. Karl Friedrich Weitzmann’s Harmonic Theory in Perspective. Dissertação
(Doutorado) - Columbia University in the City of New York, New York, EUA, 1992. SCHENKER, Heinrich. Harmony. Chicago: University of Chicago Press, 1954. SCHOENBERG, Arnold. Harmonia. São Paulo: Editora UNESP, 2001.
. Structural Functions of Harmony. New York: W.W. Norton & co., 1969.
. Funções estruturais da harmonia. São Paulo: Via Lettera, 2004.
. The Musical Idea and the Logic, Technique, and Art of Its Presentation. New York: Columbia University Press, 1995.
WEBER, Gottfried. The Theory of Musical Composition, treated with a view to a naturally conse- cutive arrangement of topics, Vol. I. London: Messrs. Robert Cocks and Co., 1851.
ZAMACOIS, J. Tratado de armonia, Volume 1. Barcelona: Labor, 1984.
. Tratado de armonia, Volume 2. Barcelona: Labor, 1988.
. Tratado de armonia, Volume 3. Barcelona: Labor, 1990.
![]()
Marcus Alessi Bittencourt (n. 1974) - Compositor, pianista e musicólogo teórico brasileiro natural dos Estados Uni- dos da América. É doutor e mestre em Composição Musical pela Universidade Columbia de Nova York e bacharel em Música pela Universidade de São Paulo. Atualmente é professor de Composição, Teoria e Computação Musical na Universidade Estadual de Maringá, Brasil.
![]()
![]()
154
![]()