

Revista Música Hodie, Goiânia - V.12, 302p., n.2, 2012
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
Prática de Notação de Música Complexa
tação rítmica.
This paper is designed to address the notational practice of complex music. Specifically I suggest that music notational practice adhere to the fundamental principle of: the number of beams/flags of any note is dependent upon the number of iterations per (di- visions of) temporal unit. For example, this principle suggests that in accepted musical prac- tice two or three equal divisions per quarter note are notated using eighth notes; while four to seven equal divisions per quarter note are notated using sixteenth notes, etc.
In the first instance this may seem obvious, since this principle forms the basis of rational rhythmic notation in music (and one of the first things music students are taught when beginning to learn an instrument or to sing). However, with music featuring nested tuplets of two levels or more, an interesting phenomena begins to occur, in which the divi- sions of a unit (or speed of movement) becomes decoupled from the expectations of rhyth- mic ratios, such as three in the space of one (see Example 1).
Example 1: A decoupling between ratio and division of unit.
This separation between divisions of unit and those of ratio becomes more press- ing as we compose and perform music featuring higher nested values (see Example 2). Due to its basis in linear mathematics, I will suggest in the first part of this paper that the num- ber of iterations per (divisions of) unit take precedence over the expectations of ratios when such mismatches occur.
Revista Música Hodie, Goiânia - V.12, 302p., n.2, 2012
![]()
258
Recebido em: 00/00/2012 - Aprovado em: 00/00/2012
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.

Example 2; Complex rhythmic notation obscuring traditional pulse-based divisions of a unit.
Every musician trained or not, quickly learns to notate temporal indications as pre- cisely as is needed to faithfully reproduce his/her intentions. These intentions most often are focused on performance, but there is a considerable body of knowledge related to com- positional integrity that may or may not presume performance as the best end result. But no matter whether intended for human performer, computer playback or theoretical specu- lation, complex rhythms should not be seen as a vacation from the rational basis of music (unless, of course freedom is notated into the score). Next I will present a few basic details.
Music notational practices in the west are relatively efficient in their representation of temporal and pitch material, less so with timbre. Typically, western temporal notational practices are fundamentally based upon divisions of a larger unit, and it is accepted that ev- ery rhythm must feature the correct number of notes with the corresponding beams or flags.
Ratio 3:1 X = not nor
![]()
Example 3: Rhythmic notation indicated by iterations over temporal unit with correct number of beams and/or flags.
In the Example 3, three equally-spaced iterations against one quarter note will use three notes with the correct number of flags or beams (see Example 3). If either the number of iteration or the speed of beaming is incorrect, then the composer/arranger risks the irri- tation of the performer and the disregard of his/her colleagues. Perhaps this example seems ridiculous in a paper presuming to talk about complex notational procedures, but it does serve to clearly reveal how important and fundamental the principle of correctly linking the number of iteration with beams or flags is embedded in our musical sub-consciousness.
The basic principle of divisions of a unit follows that the number of beams or flags will correspond with the group to which an iteration belongs as an aid to identify the speed of movement, whether complete, incomplete or unfulfilled (KOSTKA & PAYNE, 2008) (see Example 4).
Correspondence between flags/beams and divisions/iterations per quarter note | |||||||
| 1/4 | 1 to 1.999... | per quarter note |
| 1/32 | 8 to 15.999... | per quarter note |
| 1/8 | 2 to 3.999... | per quarter note |
| 1/64 | 16 to 31.999... | per quarter note |
| 1/16 | 4 to 7.999... | per quarter note |
| 1/128 | 32 to 63.999... | per quarter note |
Example 4: Number of beams/flags correspond with group to which iteration belongs.
![]()
259
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
I propose that the notation of divisions of unit or speed of movement applies to not only complete tuplet statements, but also to any members of incomplete or unfulfilled tu- plets (see Example 5).
- Complete - Incomplete - Unfulfilled

Example 5: Borrowed tuplets correspond to grouping whether complete or incomplete.
A separate convention commonly used in modern western music notational prac- tice suggests that the number of beams/flags for borrowed values are based upon gener- ally agreed upon ratios, such as three in the space of two (3:2) having the same value. In Example 6 I have identified a few common ratios (see Example 6).
However, some music presents a mismatch between the rhythmic value suggested by the ratio and the number of iterations (divisions) per unit. In the following section I will
provide evidence and rationale for suggesting that division should trump ratio.
Ratios | ||
2:3 | same value |
|
1:3 | 1 smaller value |
|
1:5 (1:6, 1;7) | 2 smaller values |
|
1:9 (1:10, 1:11, 1:12, 1:13, 1:14, 1:15) | 3 smaller values |
|
Etc. | Etc. | Etc. |
Example 6: Conventions of close approximation for closely related beam/flag values for same or adjacent groupings.
a unit.
Next I will present seven steps that examine ratio versus extrapolated divisions of
In Example 1 and again in Example 7 we wish to calculate the correct beaming val- ues for three equally spaced divisions of the final eighth note of a triplet spanning the du- ration of one quarter note (see Example 7).![]()
260
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.

Example 7: The division of inquiry consists of three equally spaced divisions of the final eighth note of the larger triplet.
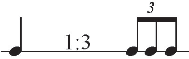
Example 8: Intuitive linear ratios - see Example 6.
As seen in Example 6, linear ratios provide a wealth of intuitive expectations in our performance and understanding of rhythm. Example 8 shows the expected relationship between a prime value (quarter note) and its division into three equal parts (triplet) (see Example 8). This rule suggests that we expect an equal three-part division to carry a value of one beam/flag more than its prime (see Example 6).
This next step is crucial to the determination of speed of movement by which a performer will move the fingers or a singer to articulate a passage. As we will see short- ly, when using nested values at two or more levels, such divisions will not always agree with the expectations of simple ratios (such as the 3:1). We do this by noting the number of equally spaced divisions of the relevant subdivision and then extrapolating (or multiplying) these divisions across the larger unit. For example, in Example 9a, the 3 divisions of the last eighth note of a triplet are shown; then in Example 9.b equal divisions of the middle and last eighth notes are shown (with a sum of 6 iterations); followed by Example 9.c in which equal divisions of the first, middle and last eighth notes are shown (for a sum of 9 iterations).
|
|
|
a. 3: last 8th | b. 3: middle and last 8ths | c. 3: first, middle and last 8ths |
Example 9: Extrapolation of a nested triplet over a quarter note duration, so that the speed of each iteration equals 9-let.
Example 10 shows a graphic representation of Example 9, parts a, b and c (see
Example 10).
1 | 2 | (3) | ||
1 | 2 | 3a | 3b | 3c |
Example 10.a: Graphic representation of Example 9, in which a nested triplet (3:1) is presented within a larger triplet, which is then extrapolated out across a full quarter note on the last eighth.
![]()
261
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
1 | 2 | (3) | ||||
1 | 2a | 2b | 2c | 3a | 3b | 3c |
Example 10.b: Graphic representation of Example 9, in which a nested triplet (3:1) in presented within a larger triplet, which is then extrapolated out across a full quarter note on the middle and final 8ths.
1 | 2 | (3) | ||||||
1a (1) | 1b (2) | 1c (3) | 2a (4) | 2b (5) | 2c (6) | 3a (7) | 3b (8) | 3c (9) |
Example 10.c: Graphic representation of Example 9, in which a nested triplet (3:1) in presented within a larger triplet, which is then extrapolated out across a full quarter note on the first, middle and final 8ths.
Three equally spaced divisions multiplied by three sub-units equal nine divisions of the quarter note (3x3=9). This calculation is shown through graphically in Example 11 below.
eighth note one | eighth note two | |||||||
Triplet one | Triplet two | Triplet three | ||||||
(1) | (2) | (3) | (4) | (5) | (6) | 7 | 8 | 9 |
![]()
Example 11: One triplet (3:1) is nested within a larger triplet, which is prolonged over a quarter note.
In Example 7, the speed of iteration when extrapolated across the duration of a quarter note would equal nine divisions of that quarter note and therefore require three beams or flags and not two as is shown in table one.
Nine equally-spaced divisions of a quarter note require beams/flags of 32nd note value (see Example 4).
The linear ratio suggests that three equally spaced divisions over the final eighth note of a triplet will carry the values of 16th notes (see Example 6). Example 12.a shows the notation of the final triplet using the logic of linear ratios. Since rhythmic notation is based upon rationale values, let’s assume this will hold true for all other linear 3:1 ratios with the result shown in Example 12.b.
|
|
12.a Linear ratio | 12.b substitution via linear ratio of all three parts of triplet |
Example 12: Linear ratio substituting 3 in the space of 1 in 12a, then in 12b continuing over the remaining two triplet 8ths.
![]()
262
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
In Example 12.b we have an example of a mismatch between ratio and divisions of a unit, as the linear substitution of the 3:1 ratio requires 16th note values, but clearly we have nine equally spaced divisions of the quarter note, which requires 32nd note beams/ flags (see Example 12).
In Example 13, we have extrapolated the notes of the nested triplet over the full du- ration of one quarter note. The resultant beam/flag values will come from the extrapolated division of the quarter note and not the intuitive expectation of the simple ratio, resulting
in beam/flag of 32nd note values (see Example 13).
|
|
13.a Divisions of unit | 13.b extrapolation of division over governing unit |
Example 13: Same speed as Example 12 with extrapolated values over the entire quarter note, resulting in 9 equal divisions.
Example 14 presents a non-controversial case. As has been seen in hundreds of years of practice and one of the earliest principles of music fundamentals, nine equally spaced divisions against a quarter note requires three beams/flags (see Example 14).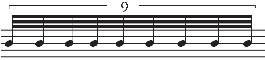
Example 14: Nine equal divisions of a quarter note require three beams/flags
Now, let us compare the logic of ratios versus that of divisions per unit. In Example
15.a the ratio of 3:1 has been extended over the entire triplet. In Example 15.b, a 9:1 fig- ure has been presented. Both Example 15.a and 15.b carry the same speed. As is common knowledge, nine divisions of a quarter note require 32nd note values. Both Example 15.a and
15.b feature nine equally spaced divisions of the quarter note, but the notation of 15.a sug-
gests a slower speed of movement, and can thus become confusing.
|
|
15.a. Ratio substitution | 15.b. Nine equal divisions of quarter note |
Example 15: Comparison of nine equal divisions of quarter note with those of ratio substitution – the values of ratio substitution are too slow.
In Example 16.a, the extrapolated division of nine equally spaced iterations is notated using 32nd notes, according to the grouping principle identified in Example 4. In Example 16.b, a 9:1 ratio has been presented again. Both Example 16.a and 16.b carry the same speed, and both use 32nd note values. Since the number of division per unit is equal, and the numbers of beams/flags are equal, we expect that the speed of movement will be the same – and they are.![]()
263
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
|
|
16.a. Extrapolated divisions of nested triplet | 16.b. Nine equal divisions of quarter note |
Example 16: Comparison of 9 equal divisions with those calculated through extrapolated divisions of quarter note.
This paper presumes that the temporal characteristics of music are logical and pre- sumes a rationale basis for its temporal characteristic. In such cases, with all things being equal (tempo, meter, etc), we can expect rhythmical values to have a prescriptive notion on performance that is, allowing for human variability, more or less perceptually reproducible. Therefore, if rhythmic accuracy is to be intended, then I would suggest that extrapolated divisions of nested tuplets assume a predominant concern, rather than relying on intuitive notions of ratio.
Points one through six have presented methods for notating complex rhythms, us- ing either ratios or divisions of the quarter note. As previously mentioned, there are in- stances when ratios decouple from equally spaced divisions of a unit. Specifically, we have compared a) linear ratios, with b) extrapolated equally-spaced divisions of a unit and have found that the substitution of one value for another (3:1) within a ratio produces in non- linear contexts illogical irregularities that are decoupled from fundamental divisions of a unit (quarter note). Next I will explore a real-world reason why composers should at- tempt to notate such practices in a way that accurately represents the speed of movement in performance.
I always compose as if I’m playing or singing. One thing I notice is the speed by which my fingers must move around a keyboard, clarinet or double bass. Next I would like to present an example that clearly demonstrates a deficiency in the performance of a nota- tion based upon ratio rather than extrapolated divisions of a unit. In Example 17 we begin with the same example of a triplet in the space of the last eighth note of a triplet lasting the duration of one quarter note that is followed by eight equal divisions of a lasting a duration
of a second quarter note (see Example 17).
Quarter note 1 | Quarter note 2 | |||||||||||
8th note 1 | 8th note 2 | 8th note 3 | 8th note 4 | |||||||||
Triplet 1 | Triplet 2 | Triplet 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
1 (2,3) | 4 (5,6) | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
![]()
Example 17: Extrapolated division of quarter notes one and two.
In Example 18, the speed at which performers will move their fingers (and for the listener, articulated cilia) for the final nested tuplet will be approximately at the rate of nine iterations per quarter note (taking into account performer variability), which will require three beams/flags. Calculated in terms of relative speed, if the quarter note = 60, then each of the nine iterations will be produced at a speed of 540 articulations per second, and thus each member of the final triplet will carry this speed; while the initial eighth note figures will be produced at the speed of 180 bpm. In Example 18.b, eight equal divisions will re- quire three beams/flags; or in terms of speed, if quarter note = 60, then eight iterations per![]()
264
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
quarter note will each be produced at a speed of 480 articulations per second, or slower than the previous triplet figure (see Example 18).
In Example 18, I present a notation in which the ratio of three in the space of one (3:1) will take precedence. As I have noted above, the final three notes of Example 18.a are moving at a faster rate (assuming quarter note = 60; 540 bpm) than the eight notes of Example 18.b (480 bpm). However, the notation here would suggest to the performer to play the final triplet of Example 18.a slower than 18.b, even though they are clearly faster. For the performer this will surely be a point of confusion and contention.
A. B.

Example 18: Decoupling of ratio from extrapolated division of quarter note, with the end result that the quicker moving notes of the final triplet in 18.a are notated using slower moving rhythmic values than in 18.b.
In Example 19.a, a notation is presented in which the division of three in the space of one is extrapolated across the larger unit (quarter note). As we have discussed above, the iteration of nine divisions per quarter note will require three beams/flags. Assuming a quarter = 60, each note of the final triplet will move at the rate of 540 bpm. In Example 19.b, each note of the eight note division will require three beams/flags, and will move at the rate of 480 bpm. Both the final triplet and the eight divisions of the following quarter note will require 32nd notes. This agrees with Example 4 and will not violate a fundamental principle of rhythmic notation that suggests faster moving notes must use beams/flags of an equal or greater value, but not slower (see Example 19).
A. B.
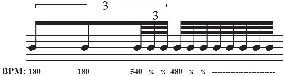
Example 19: Decoupling of ratio from iteration, in which value of iteration takes precedence and does not violate fundamental tenant that faster moving notes will use temporal values equal to or greater than slower moving notes.
Musical practice consists of, among other things, patterns and ratios across many of the dimensions that sound carries. Sometimes these ratios, when nonlinearities are in- troduced into the system, produce non-logical and unhelpful suggestions as to performance practice. As a result it might be useful to check ratios in music featuring two or more levels of nested tuplets against extrapolated equally-spaced divisions.
So far, this paper has focused on a relatively simple example of nested tuplets (trip- let within a triplet) in order to lay out what seem to be a few important principles in notat- ing rhythmically complex music, chief among them involve the extrapolation of incomplete divisions of a unit, in order to determine the correct classification of beam/flag. However, anyone reading this paper will know that most music featuring complex rhythmic material often investigates far more unusual and musically irrational values. The remainder of this paper will look to a few examples of how methods of extrapolation may serve performance
clarity and compositional generative procedures.![]()
265
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
The principle of extrapolated division remains the same when using larger values, such as when 3 iterations are placed against 1 half note. As was shown directly above, the extrapolation of the small triplet to extend over the full duration of the quarter note pro- duces a visual representation more intuitively linked with the notion of speed of movement. In this specific case, the speed of iterations per quarter note equals 4.5 and thus requires 2 beams/flags (see Example 20).
|
|
20.a. Ratio – too slow | 20. b. Extrapolated division – good fit |
Example 20: Values for a nested triplet within a larger triple – this time extended over the duration of a half note.
As proof, a graphic representation is shown in Example 21, which is essentially a temporal transposition of Example 1. This graphic shows that 9 iterations per half note will give the performer 4.5 iterations per quarter and thus the 16th note value is required.
Quarter note one | Quarter note two | |||||||
Triplet one | Triplet two | Triplet three | ||||||
1 | 2 | 3 | (4) | (5) | (6) | (7) | (8) | (9) |
Example 21: A doubling of the values from above - as expected the same ratio occurs.
Rhythmic ratios suggest that 3 iterations may substitute for 2 iterations using an equal number of beams/flags. However, this is not always the case as nested tuplets often introduce nonlinearities which serve to decouple ratio from division. In the following case the tuplet speed of 3:2 would suggest using the equal number of beams/flags (see Example
22), however, by noting the extrapolation of the smaller triplet, we obtain 4 1/3 iterations per quarter (see Example 23).
|
|
|
22.a. Triplet | 22.b. 3:2 using ratio substitution (too slow) | 22.c. 3:2 extrapolation (speed is better fit) |
![]()
Example 22: Close approximation begins to break down, relative to absolute speed at a single level nesting.
Example 22 shows the proof that the 16th note values are a more appropriate repre- sentation of the speed of movement (see Example 22). By extrapolating equal value lengths from the embedded triplet, the graphic in Example 23 clearly shows 4.33 iterations per quarter note (see Example 23).![]()
266
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
Eighth note one | Eighth note two | |||
Triplet note one | Triplet note two | Triplet note three | ||
1 | 2 | 3 | (4) | (1/3) |
Example 23: Graphic representation of a nested 3:2 within a triplet. The speed equals 4 & 1/3
Now I will move to more complicated notational practices as seen in composi- tion. In the following example from Ferneyhough: Bone Alphabet, m. 27, both sextuplets, each lasting 1/6 of the bar, use one beam too few when extrapolating these divisions across the full duration of the quarter note (FERNEYHOUGH, 1995). Embedded within a triplet against two eight note values, each sextuplet lasts 1/6 of a quarter note value. Example 24 shows Ferneyhough’s notation above, while underneath the notation based upon linear pro- longation of the sextuplet (see Example 24).
original rhythmic values |
6: 1/16 + 6: 1/16 + 5: 1/8 + 5:1/8 |
rhythmic values according to linear prolongation of division |
6: 1/16 + 6: 1/16 + 5: 1/8 + 5:1/8 |
Example 24: 6tuplets within a larger triplet from Ferneyhough: Bone Alphabet, m. 27. According to the principle of linear extrapolation of the 6tuplet division, the excerpt above features 1 beam too few (36 divisions per quarter
= 5 beams).
Example 25 shows the linear prolongation of a sextuplet over the duration of two eighth notes (or one quarter). Each sextuplet will be calculated as.5 of one triplet leg, and thus one-sixth of a quarter note. The extrapolated value will equal 6 x 6 iterations, or 36 di- visions per quarter, requiring 128th notes (5 beams/flags) (see Example 25).
Eighth note one | Eighth note two | ||||||||||||||||||||||||||||||||||
Triplet, part 1 | Triplet, part 2 | Triplet, part 3 | |||||||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
![]()
![]()
![]()
Example 25: A 6tuplet figure lasting 1/6 of a quarter note is linearly prolonged over the duration of 1 complete quarter note. The prolongation results in 36 iterations (6 x 6) per quarter note which requires 128th notes (5 beam lines).
Example 26 shows the absolute speed of each quintuplet within stems two and three of the larger triplet. As is shown, the absolute speed will equal 5 x 3 or 15 iterations per quarter note and will require 32nd notes, which is in agreement with the Ferneyhough notation (see Example 26).![]()
267
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
Eighth note one | Eighth note two | |||||||||||||
Triplet, part 1 | Triplet, part 2 | Triplet, part 3 | ||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
![]()
![]()
![]()
Example 26: Linear prolongation of quintuplet figure(s) each lasting 1/3 of one quarter note value - 15 iterations
(5 x 3) per quarter note = 32nd notes (3 beam lines).
In this and the following examples, I will discontinue the comparison between rhythmic values calculated according to ratio and those though prolongation of division, as the intuitive sense of rhythmic ratio relationships become less obvious with higher level nested values, and in my perception increasingly a non-issue.
Example 27 analyses a rhythmic passage from Ferneyhough: Bone Alphabet m. 116, in which I will recalculate the 7:5 division. In Example 27 the triplet extends over the du- ration of an eighth note, while the following quintuplet also extends over an eighth (see Example 27).
|
|
27.a. Original rhythmic notation | 27.b. Rhythmic notation according to prolongation of division |
Example 27. Original and recalculated notation of a nested 7:5 of a larger triplet.
In the graphic below the 7:5 ratio is worked out in the following way:
• The top row identifies a space of an 8th note.
• The 2nd row identifies the triplet which lasts the duration of an eighth note.
• The 3rd row identifies the 6 subdivisions of the triplet (observe that the 32nd rest equals 1/6 of the 8th note, while the remaining 5/6 of an 8th note are the 5 of the 7:5).
• The fourth row identifies the initial rest (1/6 of the 8th note), followed by 7 in the
space of the previous 5.
• The fifth row prolongates the 7 iterations across the initial 32nd rest value. Since each 7-let equals 5/7 of each sextuplet, the absolute speed of the 7-let equals 8
2/7 per 8th note (or 16 4/7 per quarter, which requires the 64th note value – or 4![]()
beams) (see Example 28).
1/8 | |||||||||
Triplet, part 1 | Triplet, part 2 | Triplet, part 3 | |||||||
1 (rest) | 2 | 3 | 4 | 5 | 6 | ||||
1 (rest) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
1/7 | 2/7 | (8) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
![]()
Example 28: The ratio of 7:5 nested within a larger triplet is shown graphically.
![]()
268
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
The following is from J. Eckhardt: 16, m 161 (ECKARDT, 2003). In this example, I will renotate the quintuplet (5:4) nested within an 11:6 ratio according to the principle of linear prolongation of the divisions under the 11:6 figure (see Example 29).
|
|
29. a. Original rhythmic notation | 29.b. Rhythmic notation according to prolongation of division |
Example 29. Original and recalculated notation of a nested quintuplet within the higher 11:6 strata.
In Example 30 the ratios are worked out in the following way:
• The top row identifies a space of the first two 8th notes.
• The 2nd row identifies the eight subdivisions implied over the first two 8th notes.
• The 3rd row identifies the 64th and dotted 32nd notes.
• The 4th row shows the placement of 11 iterations against 6.
• The 5th row shows the duration of the 16th note values that begin and end this figure (comprising iterations 1+2 and 10+11).
• The 6th row shows the placement of the quintuplet figure (5:4) that align with
iterations 6 through 9 of the original 11 note figure.![]()
![]()
![]()
• The 7th row shows once again the ratio of 11:6 (against iterations 3 through 8 of the original). 8). The 8th row reconfigures the value of 5:4 within the 11:6 ratio by prolongating in reverse the 5:4 twice from the end of the second 8th note. The resulting placement equals approximately 9 1/5 iterations per 8th or 18 2/5 per quarter. These will require 64th note values or 4 beams (see Example 30).
Eighth note one | Eighth note two | |||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||||||
1 | + 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||||||
1 | + 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
1 | + 2 | 1 + 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 + 11 | ||||
1 | + 2 | 1 + 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 10 + 11 | |||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||||
10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
![]()
![]()
Example 30: A graphic representation of a nested quintuplet with the higher 11:6 strata
Mental Rap
The following examples are from my Tempo Mental Rap, variation 6, page 40 (EDGERTON, 2005). Embarrassingly, this excerpt features SIX discrepancies when com- pared with the linear extrapolation of division across a quarter note (see Example 31).![]()
269
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
|
Original rhythmic notation |
|
(see Ex. 32 33 34 35 36) Renotation of rhythmic notation according to prolongation of division |
Example 31: Discrepancies in a passage from my Tempo Mental Rap and its renotation using prolongation procedures.
In Example 32 the ratios are worked out in the following way:
• The top row identifies a space for the half note.
• The 2nd row identifies each quarter.
• The 3rd row identifies each 8th note.
• The 4th row identifies 14 iterations against one half.
• The 5th row shows the ratio 5:4 within the nested 14 iteration value.
• The 6th row shows the ratio 7:3, nested under the 5:4 ratio.
• The 7th row shows the 7-lets prolongated across one quarter note value. As can be seen the resulting value is 20.5 per quarter note, which will require 64th notes, not 32nd (see Example 32).
14: | |||||||||||||||||||||
|
| ||||||||||||||||||||
|
|
|
| ||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||
1 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | (7:3 under 5:4 = 20.5, needing 64th note values) |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Example 32: A graphic representation of the nested ratio 7:3, within a larger 5:4, within the borrowed value of
14: half note and prolonged across one quarter note.
In Example 33 the ratios are worked out in the following way:
• the top row identifies a space for four 8th notes.
• The 2nd row identifies 14 iterations against one half.
• The 3rd row shows the ratio 5:4 within the nested 14 iteration value.![]()
270
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
• The 4th row shows the subdivision of iteration #4 of the quintuplet (highlighted).
• The 5th row shows a prolongation of the quintuplet to twice its original value, so that it spans across one quarter note value at the rate of 8.75 iterations per quarter note (3 beams/flags).
• In the 6th row each iteration of the prolonged quintuplet is subdivided. When
prolongated to a quarter note value, there are 35 iterations which requires 128th
notes (5 beams) (see Example 33).
Also in Example 33, the original notation features a 16th note rest – this should have the value of a 32nd note rest, as it occupies 1/5 of the 5:4 quintuplet. As was indicated direct- ly above, the quintuplet when prolongated over a quarter note value will feature 8.75 itera- tions (see Example 33).
Eighth note one | Eighth note two | Eighth note three | Eighth note four | ||||||||||||||||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |||||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | rest | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||||||||||||||||||||||||
9 | 10 | 11 | 12 | 13 | 14 |
![]()
![]()
![]()
![]()
![]()
![]()
Example 33: A graphic representation of the subdivision of the nested ratio 5:4, within the borrowed value of 14:
half note, and prolonged across one quarter note.
In Example 34 the ratios are worked out in the following way:
• The top row identifies a space for each 8th note.
• The 2nd row identifies 14 iterations against one half.
• The 3rd row shows the ratio 7:6 within the nested 14 iteration (#5 through 10)
value.
• The 4th row shows the ratio 5:3, nested under the 7:6 ratio.
• The 5th row takes two steps back and shows the original 14 note division of the half note.
• The 6th row shows the ratio 7:6 twice, in order to prolongate the iterations across
a quarter note value.
• The 7th row shows the ratio 5:3 prolongated across the quarter note value. This results in approximately 13.6 iterations per quarter note, which will require
32nd note values and not 16th note values (see Example 34).
Eighth note one Eighth note two Eighth note three Eighth note four
1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 1 2 3 4 5 6 7 11 12 13 14
1 2 3 4 5 1 2 3 4 5 4 5 6 7 11 12 13 14
1 2 3 4 5 6 1 2 3 4 5 6 13 14
1 2 3 4 5 6 7 1 2 3 4 5 6 7 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13 14 (15) (16) (17) (18) (19) (20) 13 14

Example 34: A graphic representation of the nested ratio 5:3, within a larger ratio of 7:6, within the borrowed value of 14: half note and prolonged across one quarter note.
![]()
271
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
In Example 35 the ratios are worked out in the following way:
• The top row identifies a space for each 8th note.
• The 2nd row identifies 14 iterations against one half.
• The 3rd row shows the ratio 7:6 within the nested 14 iteration value.
• The 4th row shows the division of integers 4 and 5.
• The 5th row shows the original 14 iterations against one half.
• The 6th row prolongates the 7-lets prolongated across one quarter note value.
• The 7th row shows the division of each 7-let, which amounts to approximately
16.4 iterations per quarter note, which will require 64th notes, not 16th notes (see
Example 35).
From there we know also the exact value of the iterations found within #6 and 7 within the 7-let, as these are simply double the speed of the previous two iterations, #4 and
5. Therefore the iterations, if prolongated would equal approximately 32.8 per quarter note,![]()
![]()
![]()
which will require 128th notes, not 64th notes.
Eighth note one | Eighth note two | Eighth note three | Eighth note four | ||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||||||||||
1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 11 | 12 | 13 | 14 | |||||||||||||||
1 | 2 | 3 | 4 | + | 5 | + | 6 | 7 | 11 | 12 | 13 | 14 | |||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 13 | 14 | ||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
![]()
![]()
![]()
![]()
![]()
Example 35: A graphic representation of the division of the nested ratio 7:6, within the borrowed value of 14: half note and prolonged across one quarter note.
In Example 36 the ratios are worked out in the following way:
• the top row identifies a space for each 8th note.
• The 2nd row identifies 14 iterations against one half.
• The 3rd row shows the ratio 3:2 within numbers 13 and 14 of the nested 14 itera- tion value.
• The 4th row is empty.
• The 5th row shows the final 7 iterations of the original 14 note iteration.
• The 6th row prolongates the 3:2 ratio across one quarter note. This results in 10 and 1/3 iterations per quarter note, and will require 32nd notes, not 16ths (see Example 36).
Eighth note one Eighth note two Eighth note three Eighth note four
1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3
8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1/3 |

Example 36: Representation of a nested ratio 3:2 under a value of 14: half note which is prolonged across a quarter note.
![]()
272
![]()
EDGERTON, M. E. Notational Practice of Complex Music. Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 258-273.
In Example 37 a graphic representation of all nested levels shown in Example 31 are shown.
Eighth note one | Eighth note two | Eighth note three | Eighth note four | |||||||||||||||||||||||||||||||
rest | rest | rest |
![]()
|----------------7:3--------------| |----------------5:3----------------| |-----------3:2------------|
|----------------------------5:4---------------------------| |-------------------------------------------7:6------------------------------------------|
|-------------------------------------------------------------------------------------------------14: Half Note--------------------------------------------------------------------------------------------------|
Example 37. A graphic representation of Example 31.
In this paper I show that the speed of beams/flags found in music featuring non- linear and nested tuplets often feature a decoupling between a) the linear extrapolation of divisions of a unit (quarter note) and, b) rhythmic ratios. In such cases, I propose that it is worthwhile to calculate the speed at which a musical passage is moving, in order to check the appropriateness of a notation. Figures 18 and 19 present a clear example of a decoupling between ratio and extrapolation of division. After a cursory examination of the gesture in- volved I found that substitution by ratio produced a notation that inverted the speed of mo- tion relationship in which faster moving notes (540 bpm) featured slower rhythmic values (16th notes), whereas extrapolation of division produced beaming relationships that repre- sented the speed of movement more faithfully.
When two, three or more nested levels are present it may be exceedingly difficult to internalize an intuitive sense of rhythmic ratios, rendering the discussion as to the ap- propriateness of one method over the other somewhat irrelevant. In examples 24 - 37, I have discontinued any discussions of ratio, due to the level of overall complexity and focused solely on extrapolation of division.
2012, May 11, Kuala Lumpur
REFERENCES
ECKARDT, Jason. 16. For amplified flute and string trio. New York: Carl Fischer Music, 2003. EDGERTON, Michael. Tempo Mental Rap. For guitar. Score. Berlin: manuscript, 2005. FERNEYHOUGH, Brian. Bone Alphabet. For solo percussion. London: Edition Peters, 1995. KOSTKA, Stefan; PAYNE, Dorothy. Tonal Harmony. 6. ed. New York: McGraw-Hill, 2008. 736p.
![]()
![]()
![]()
273
![]()