Revista Música Hodie, Goiânia - V.12, 302p., n.2, 2012
Definição de Sintaxe Composicional a Partir do Estabelecimento de Hierarquias Entre Sonoridades Tricordais Relacionadas por Similaridade
Weskley Dantas (UFCG, Campina Grande, PB, Brasil)
weskley.dantas@gmail.com
Liduino Pitombeira (UFCG, Campina Grande, PB, Brasil)
pitombeira@yahoo.com
Resumo: Neste artigo é descrito o processo de definição de um sistema composicional que estabelece relações hierárquicas entre conjuntos de classes de notas tricordais a partir da similaridade entre seus vetores intervalares. Inicialmente, com base no modelo de cálculo de similaridade proposto por Lewin, é construída uma tabela para cada tricorde, que relaciona todos os tricordes pelos seus índices de similaridade, dividindo-os em classes. Em seguida, realizamos um breve exame do conceito de sistemas simbólicos e de sua aplicabilidade no domínio da música, o que nos possibilitou formalizar o sistema composicional que foi a base para o planejamento da obra Temperamentos, para quarteto de cordas. Palavras-chave: Similaridade vetorial; Sistema composicional; Temperamentos.
Definition of a Compositional Syntax from the Establishment of Hierarchies Among Trichordal Sonorities Related by Similarity
Abstract: In this article, we describe the process of defining a compositional system that establishes hierarchical relationships between trichordal set classes based on the similarity between their interval vectors. Initially, based on the similarity calculation model proposed by Lewin, a table is constructed for each trichord, which relates one to another by their similarity indexes, organizing them into classes. Next, we performed a brief survey of the concept of symbolic system and its applicability in the field of music, which enabled us to formalize the compositional system that was the basis for the planning of the work Temperamentos, for string quartet. Keywords: Vectorial similarity; Compositional system; Temperaments.
São diversos os critérios que definem similaridades entre conjuntos de classes de notas. A própria organização das 4096 possibilidades combinatoriais no âmbito da gama cromática de doze classes de notas (em conjuntos de três, quatro, cinco, até o limite de nove classes de notas), realizada por Allen Forte (1973)1, agrupa esses conjuntos por relações de similaridade transpositiva e inversiva, denominados posteriormente, por Straus (2000, p. 47) e Roig-Francolí (2008, p. 82) de classes de conjuntos de classes de notas (set classes). Mesmo assim, têm-se buscado ampliar as relações de similaridade com o objetivo de detectar coerência sintática do uso de conjuntos pertencentes às mais diversas classes de conjuntos de classes de notas. Vários autores, além de Forte, já trataram desse tema. Entre eles podemos citar Chrisman (1971), Morris (1979), Lewin (1979-80), Scott e Isaacson (1998), Buchler (2000) e Isaacson (1990).
Isaacson (1990) examinou diversos modelos utilizados para o cálculo de similaridade (Forte, Rahn, Lord, Morris, Lewin e Teitelbaum) e, propôs um novo modelo, que é baseado em Teitelbaum e que consiste, basicamente, no cálculo do desvio padrão da diferença entre os vetores intervalares entre dois conjuntos de classes de notas. No entanto, como o modelo de Lewin produz mais classes de similaridade, optaremos por utilizá-lo na definição de nosso sistema composicional.
O modelo de Lewin, cuja fórmula corrigida é fornecida em Isaacson (1990, p. 11), calcula a similaridade entre conjuntos de qualquer cardinalidade, com base nos vetores intervalares de ambos os conjuntos. Nesta fórmula (figura 1), xi e yi correspondem respectivamente aos vetores intervalares dos conjuntos X e Y, e #X e #Y correspondem às quantidades de classes de notas dos conjuntos X e Y, respectivamente.
Revista Música Hodie, Goiânia - V.12, 302p., n.2, 2012 Recebido em: 13/04/2012 - Aprovado em: 30/05/2012
Figura 1: Fórmula de Lewin para o cálculo da similaridade entre dois conjuntos de classes de notas.
A partir desta fórmula (Figura 1), determinaremos os índices de similaridade entre todos os tricordes, uma vez que nosso sistema composicional limitar-se-á ao uso de conjuntos de classes de notas tricordais. A Tabela 1 mostra o índice de similaridade de todos os tricordes entre si. O índice de similaridade máximo é 1 e o mínimo é 0. Esse valor é obtido cruzando-se as informações entre as linhas e as colunas da Tabela 1. Assim, por exemplo, a similaridade entre dois tricordes [012] é 1 e entre um tricorde [036], tríade diminuta, e [048], tríade aumentada, é 0.
Tabela 1: Índice de similaridade entre tricordes.
| [0, 1, 2] | [0, 1, 3] | [0, 1, 4] | [0, 1, 5] | [0, 1, 6] | [0, 2, 4] | [0, 2, 5] | [0, 2, 6] | [0, 2, 7] | [0, 3, 6] | [0, 3, 7] | [0, 4, 8] | |
| [0, 1, 2] | 1.000 | 0,805 | 0,471 | 0,471 | 0,471 | 0,471 | 0,333 | 0,333 | 0,333 | 0,000 | 0,000 | 0,000 |
| [0, 1, 3] | 0,805 | 1,000 | 0,667 | 0,333 | 0,333 | 0,471 | 0,667 | 0,333 | 0,333 | 0,471 | 0,333 | 0,000 |
| [0, 1, 4] | 0,471 | 0,667 | 1,000 | 0,667 | 0,33 | 0,333 | 0,333 | 0,333 | 0,000 | 0,471 | 0,667 | 0,577 |
| [0, 1, 5] | 0,471 | 0,333 | 0,667 | 1,000 | 0,667 | 0,333 | 0,333 | 0,333 | 0,471 | 0,000 | 0,667 | 0,577 |
| [0, 1, 6] | 0,471 | 0,333 | 0,333 | 0,667 | 1,000 | 0,000 | 0,333 | 0,333 | 0,471 | 0,333 | 0,333 | 0,000 |
| [0, 2, 4] | 0,471 | 0,471 | 0,333 | 0,333 | 0,000 | 1,000 | 0,471 | 0,805 | 0,471 | 0,000 | 0,333 | 0,577 |
| [0, 2, 5] | 0,333 | 0,667 | 0,333 | 0,333 | 0,333 | 0,471 | 1,000 | 0,333 | 0,805 | 0,471 | 0,667 | 0,000 |
| [0, 2, 6] | 0,333 | 0,333 | 0,333 | 0,333 | 0,333 | 0,805 | 0,333 | 1,000 | 0,333 | 0,333 | 0,333 | 0,577 |
| [0, 2, 7] | 0,333 | 0,333 | 0,000 | 0,471 | 0,471 | 0,471 | 0,805 | 0,333 | 1,000 | 0,000 | 0,471 | 0,000 |
| [0, 3, 6] | 0,000 | 0,471 | 0,471 | 0,000 | 0,333 | 0,000 | 0,471 | 0,333 | 0,000 | 1,000 | 0,471 | 0,000 |
| [0, 3, 7] | 0,000 | 0,333 | 0,667 | 0,667 | 0,333 | 0,333 | 0,667 | 0,333 | 0,471 | 0,471 | 1,000 | 0,577 |
| [0, 4, 8] | 0,000 | 0,000 | 0,577 | 0,577 | 0,000 | 0,577 | 0,000 | 0,577 | 0,000 | 0,000 | 0,577 | 1,000 |
A partir desta tabela, elaboramos uma nova tabela para cada tricorde de acordo com o grau de similaridade. Se observarmos, por exemplo, o tricorde [0, 1, 2] na tabela 1, veremos que alguns valores de similaridade repetem-se para diferentes tricordes, nesse caso,
0.471 para [0, 1, 4], [0, 1, 5], [0, 1, 6] e [0, 2, 4], 0.333 para [0, 2, 5], [0, 2, 6] e [0, 2, 7] e, 0.000 para [0, 3, 6], [0, 3, 7] e [0, 4, 8]. Se os tricordes serão agrupados de acordo com o grau de similaridade, teremos, então, por exemplo, cinco subgrupos para o tricorde [0, 1, 2]. A esses subgrupos chamaremos classes de similaridade. As classes de similaridade são rotuladas em ordem decrescente utilizando as letras do alfabeto (A, B, C,...). Dessa maneira, para o [0, 1, 2], os tricordes que correspondem às cinco classes de similaridade serão: A = {[012]}, com similaridade 1, B = {[013]}, com similaridade 0.805, C = {[014, 015, 016, 024]}, com similaridade 0.471, D = {[025], [026], [027]}, com similaridade 0.333 e E = {[036], [037], [048]}, com similaridade 0. A tabela 2 mostra as tabelas individuais de similaridade de cada tricorde agrupadas em quatro grupos maiores de acordo com a quantidade de classes de similaridade que cada um apresenta. O conceito de classe de similaridade cria naturalmente uma hierarquização2 quantitativa entre as sonoridades tricordais, ou seja, há tricordes com maior quantidade de classes de similaridade diferenciadas do que outros. Assim, pela Tabela 2, se observa que o tricorde [048] é o único que tem a menor quantidade de classes de similaridade (1, 0.577 e 0). Embora esse conceito possa ser ampliado para o âmbito tetracordal, pentacordal e hexacordal, neste artigo, nos restringiremos ao uso de tricordes. Essa hierarquização quantitativa será utilizada como fator decisivo na delimitação de conexão entre as sonoridades tricordais, como veremos adiante:
DANTAS, W.; PITOMBEIRA, L. Definição de Sintaxe Composicional a Partir do Estabelecimento de Hierarquias Entre Sonoridades Tricordais... Revista Música Hodie, Goiânia, V.12 - n.2, 2012, p. 109-119.
Tabela 2: Tabelas de similaridade entre tricordes e grupos de classes de similaridade.
| Tricorde com 3 Classes de Similaridade | |||||
|---|---|---|---|---|---|
| 048 | 014 | 012 | |||
| 015 | 013 | ||||
| 024 | 016 | ||||
| 026 | 025 | ||||
| 037 | 027 | ||||
| Tricorde | 036 | ||||
| Similaridade | 1 | 0,577 | 0 | ||
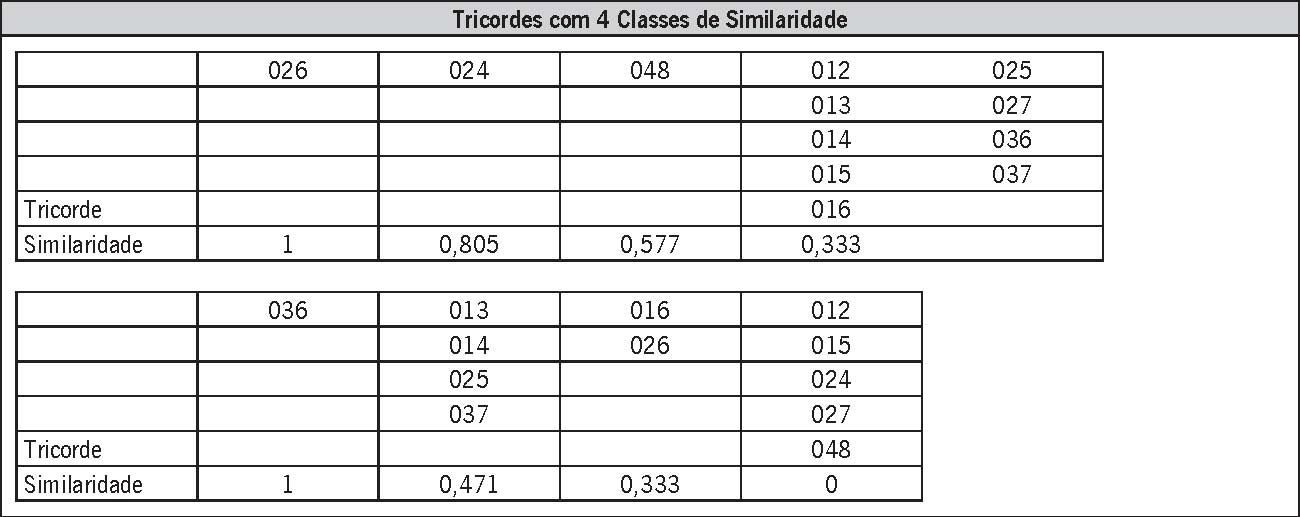
| Tricorde Similaridade Tricorde Similaridade Tricorde Similaridade | 012 1 016 1 027 1 | Tricordes com 5 Classes de Similaridade 013 014 025 015 026 016 027 024 0,805 0,471 0,333 015 012 013 027 014 025 026 036 037 0,667 0,471 0,333 025 015 012 016 013 024 026 037 0,805 0,471 0,333 | 036 037 048 0 024 048 0 014 036 048 0 |
|---|
| Tricordes com 6 Classes de Similaridade | ||||||||
|---|---|---|---|---|---|---|---|---|
| 013 | 012 | 025 | 024 | 015 | 048 | |||
| 014 | 036 | 024 | ||||||
| 026 | ||||||||
| 027 | ||||||||
| Tricorde | 037 | |||||||
| Similaridade | 1 | 0,805 | 0,667 | 0,471 | 0,333 | 0 | ||
![]()
| Tricorde Similaridade Tricorde Similaridade Tricorde Similaridade Tricorde Similaridade Tricorde Similaridade | 014 1 015 1 024 1 025 1 037 1 | 013 015 037 0,667 014 016 037 0,667 026 0,805 027 0,805 014 015 025 0,667 | 048 0,577 048 0,577 038 0,577 013 037 0,667 048 0,577 | 012 036 0,471 012 027 0,471 012 013 025 027 0,471 024 036 0,471 027 037 0,471 | 016 024 025 026 0,333 013 024 025 026 0,333 014 015 037 0,333 012 014 015 016 026 0,333 013 016 024 026 0,333 | 027 0 036 0 016 036 0 048 0 012 0 |
|---|
1. Sistemas composicionais
Trabalharemos com o conceito de sistema simbólico, proposto por Ludwig von Bertalanffy (2008, p. 84), ao inserir a música no âmbito da Teoria Geral dos Sistemas. Nessa categoria, os padrões organizam-se a partir de algoritmos simbólicos denominados “regras do jogo” (idem, p. 53). Corroborando esse conceito de Bertalanffy, podemos compreender os sistemas musicais como “conjuntos bem definidos de operações realizadas em configurações musicais” (WINHAM, 1970, p. 43). Configurações musicais são segmentos ou passagens (um termo utilizado pelo próprio Winham), cujos parâmetros (altura, ritmo,...) podem ser manipulados por meio de operações, tais como, transposição, inversão, aumentação, diminuição etc. Winham cita, por exemplo, o sistema tonal como predominantemente restrito às manipulações nos parâmetros altura e ritmo, excluindo manipulações em outros parâmetros, como dinâmica e timbre. Herbert Brun (SMITH, 1979, p. 68) exemplifica o conceito de sistema composicional, ao descrever um paralelo com as séries de instruções que se aplicam para alterar os estados on e off das 88 teclas de um piano. Neste trabalho, utilizamos a definição de sistema composicional, proposta por Lima (2011, p. 63): “um conjunto de diretrizes, formando um todo coerente, que coordenam a utilização e interconexão de parâmetros musicais, com o propósito de produzir obras musicais”. Essas diretrizes alteram os dados de entrada (alturas, ritmos, dinâmicas,...) e se relacionam entre si a partir de operações pré-definidas pelo compositor (transposição, retrogradação, inversão, aumentação, filtragem,...), bem como, a partir de decisões composicionais livres que alteram a operação do sistema. Na prática, os sistemas composicionais são estabelecidos a partir de uma série de definições, como veremos adiante na segunda seção deste artigo.
Nosso objetivo nessa pesquisa é definir um sistema composicional a partir do estabelecimento de uma sintaxe3 de conexão entre sonoridades tricordais baseada no cálculo de similaridade de Lewin. Esta sintaxe, que será detalhada na próxima seção, é decorrente da hierarquia quantitativa que resulta das classes de similaridade associadas a cada tricorde, como observamos na Tabela 2. Vale salientar com bastante ênfase, que este procedimento de hierarquização tem como única função sugerir uma lógica de conexão entre sonoridades tricordais e, portanto, não se relaciona, em nenhuma hipótese, com o estabelecimento de alturas hierárquicas, embora a centricidade de alturas não seja um procedimento alheio à música pós-tonal, como bem observam Roig-Francolí (2008, p. 2) e Straus (2000, p. 112-114)4.
2. Formalização do sistema composicional
Na formalização do sistema composicional para a composição da obra Temperamentos, para quarteto de cordas, realizaremos uma analogia com o procedimento utilizado por Allen Irving McHose (1947) para a modelagem do sistema tonal, mormente, o que foi empregado na composição dos 371 corais de Bach.
O procedimento metodológico de McHose (1947, p. 307) consistiu em um levantamento estatístico das tríades encontradas nos 371 Corais de Bach, o que o levou a observar que a tônica (I), tem um percentual de 38% de ocorrência, o V e o viio, 34%, o ii e o IV, 19%,
o vi, 7% e o iii, 2%. Em seguida, ele classificou as tríades, com exceção da tônica, em classes de acordo com critérios quantitativos, ou seja, as tríades com maior ocorrência (V e viio) seriam membros da 1ª classe, sendo seguidas pela 2ª classe (ii e IV), 3ª classe (vi) e 4ª classe (iii). Neste caso, a classe em um nível mais elevado é a 1ª, sendo seguida em ordem descendente pela 2ª, 3ª e 4ª classes. Ele também quantificou as progressões harmônicas dos corais de Bach (McHOSE, 1947, p. 308), classificando-as em quatro tipos: 1) Normal – move-se de uma classe inferior para uma classe superior, isto é, em direção à tônica. Exemplo: iii - vi -ii - V - I, podendo iniciar em qualquer grau; 2) Repetição – fica parada na mesma classe; 3) Elisão – salta uma ou mais classes em direção à tônica. Exemplo: vi - V - i; e Retrogressão – move-se de uma classe superior para uma classe inferior, isto é, em direção contrária à tônica. Exemplo: vi - iii, V - ii, V - iv.
Para oferecer um modelo de conexão triádica, McHose identificou o percentual de incidência de cada tipo de progressão nos Corais de Bach (normal – 76%, repetição – 14%, elisão – 6% e retrogressão – 4%), ampliando estes dados para outros compositores contemporâneos de Bach. Ele concluiu que os compositores do século XVIII utilizam 76% de progressão normal e 24% das demais progressões, sendo o segundo tipo de progressão (repetição) também a segunda mais utilizada por estes compositores (McHOSE, 1947, p. 10). Estas conclusões analíticas têm, evidentemente, aplicações prescritivas; ou seja, a replicação da sonoridade tonal do século XVIII, pode ser obtida ao realizarmos uma sintaxe (conexões triádicas) dentro do mesmo âmbito estatístico descrito por McHose.
No nosso caso, o sistema composicional será construído a partir de uma série de definições, precisas o suficiente para caracterizar plenamente o sistema e flexíveis o suficiente para permitir o planejamento de obras distintas. O núcleo central dessas definições é a sintaxe de conexão entre as sonoridades (Definição 4), que propõe uma analogia direta com o procedimento metodológico utilizado por McHose. A Tabela 3 fornece o conjunto de definições do sistema.
Tabela 3: Sistema Composicional.
| Definição 1 | O sistema se restringe ao controle de alturas. |
| Definição 2 | O léxico se restringe às 12 classes de conjuntos classes de notas tricordais, classificadas em grupos de acordo com a similaridade (Tabela 2). |
| Definição 3 | Os tricordes serão distribuídos tanto vertical como horizontalmente, sendo possível uma combinação dos dois formatos. |
| Definição 4 | A sintaxe é definida a partir de 4 tipos de movimento entre as classes de similaridade, que serão livremente associados a percentuais durante a fase de planejamento. Normal = movimento contíguo partindo de uma classe de menos similaridade em direção ao tricorde principal (A). Repetição = movimento interno entre os tricordes de uma única classe. Elisão = movimento não contíguo partindo de uma classe de menor similaridade em direção ao tricorde principal (A). Retrogressão = movimento partindo de uma classe de maior similaridade para uma classe de menor similaridade podendo ser contíguo ou não. |
3. Planejamento composicional
Utilizaremos no planejamento de Temperamentos a teoria dos humores corporais, desenvolvida por Hipócrates (séc. IV-V a.C) e posteriormente sistematizada por Galeno em sua monografia “De Temperamentis” (PEREIRA e GUZZO, 2002, p. 92). Os quatro humores são: melancólico (indivíduos tristes e melancólicos), sanguíneo (indivíduos atléticos e vigorosos), fleumático (indivíduos cronicamente cansados e lentos) e colérico (indivíduos facilmente irritáveis). Esses humores também foram descritos por Kant, em sua obra “Anthropology”, escrita em 1798 (idem). Cada movimento do quarteto será associado a um dos humores, com suas características, tais como são descritas por Galeno e Kant. Essas características serão associadas a parâmetros no domínio musical. A Tabela 4 mostra cada temperamento com suas características intrínsecas (de acordo com Galeno e Kant), bem como, suas possíveis equivalências musicais.
Outro critério será utilizado concomitantemente à teoria dos humores. De acordo com ele, faremos uma relação intertextual, do ponto de vista estilístico, com um compositor para cada um dos movimentos. Essa associação nos permitirá definir práticas e sonoridades associadas a esses compositores. Assim, para o primeiro movimento, que se baseará no humor melancólico, faremos uma leitura de Webern, tomando como partida, o tricorde [014], que é um importante arquétipo em sua obra (MENEZES, 2002, p. 115). Para o segundo movimento, que se baseará no humor sanguíneo, traduziremos para a dimensão tricordal as células tetracordais de Bartók (X, Y, e Z), de acordo com a definição de Antokoletz (1984,
p. 69-72). Essas células, que correspondem respectivamente aos tetracordes [0123], [0246] e [0167], serão transformadas nos tricordes [013], [026] e [016], respectivamente. O critério utilizado na tranformação é o de máxima similaridade vetorial. Nos dois primeiros casos, utilizando a fórmula de Lewin (Figura 1), obtém-se similaridade de 0,977, e no terceiro caso, a similaridade é máxima (1).
Para o terceiro e quarto movimento, fleumático e colérico, utilizaremos associações com Schoenberg e Boulez, respectivamente, através da aplicação de procedimentos atribuídos a esses compositores: combinatoriedade hexacordal inversiva (STRAUS, 2000, p. 185) e multiplicação (idem, p. 197-202).
Tabela 4: Características dos humores e suas equivalências musicais
| Humor | Características intrínsecas | Características musicais | Associações intertextuais |
|---|---|---|---|
| Melancólico | Tristeza e melancolia Emoções intensas Vagarosidade de ações | Andamento lento Retrogressão | Webern - tricorde 014 |
| Sanguíneo | Atletismo e vigor Força, rapidez Emoções superficiais | Andamento rápido Progressões normais (alta similaridade) | Bartók - células X, Y e Z |
| Fleumático | Cansaço crônico e lentidão Ausência de reações emocionais Vagarosidade de ações | Andamento lento Similaridade média-alta | Shoenber-Combinatoriedade hexacordial inversiva |
| Colérico | Irritabilidades Rapidez Impetuosidade de ações | Andamento rápido Baixa similaridade Conduções bruscas | Boulez - multiplicação |
A partir dessas equivalências, mostradas na Tabela 4, elaboramos um planejamento detalhado da microestrurtura de cada movimento. O primeiro movimento (Melancólico) é estruturado em duas camadas. A primeira camada consiste em uma linha melódica, que se move entre os instrumentos do quarteto, e é inteiramente construída a partir do tricorde [014]. A segunda camada consiste de blocos de acordes intermitentes que realizam a retrogressão dentro do âmbito do grupo de classes de similaridade do tricorde [014] (Tabela 2). Este movimento é estruturado em cinco seções, delimitadas pelas mudanças nos tricordes da segunda camada. A última seção é iniciada por um solo de violino e em seguida este movimento conclui com um trecho homofônico, onde os blocos de acordes são alongados.
O segundo movimento (Sanguíneo) é dividido em três seções simetricamente distribuídas, onde a primeira, com 30 compassos, utiliza o tricorde [013], a segunda, com 20 compassos utiliza o tricorde [026] e a terceira, com 30 compassos, utiliza o tricorde [016]. Esses tricordes se movimentam em progressão normal, de acordo com as especificações da Tabela 5. As seções são rotuladas com as letras que correspondem às células bartokianas.
Tabela 5: Estrutura do segundo movimento.
| Seção | X | Y | Z | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Compassos | 5 | 5 | 5 | 5 | 5 | 5 | 3 | 3 | 4 | 5 | 5 | 6 | 6 | 6 | 6 | 6 |
| Tricordes | 048 | 015 | 036 | 014 | 012 | 013 | 012 | 048 | 024 | 026 | 024 | 024 | 013 | 012 | 015 | 016 |
| 016 | 014 | 015 | 048 | 014 | 027 | |||||||||||
| 016 | 015 | 025 | ||||||||||||||
| 026 | ||||||||||||||||
| 036 | ||||||||||||||||
| 037 | ||||||||||||||||
O terceiro movimento (Fleumático) é construído a partir de uma série dodecafônica que se origina de um hexacorde com potencial de produzir combinatoriedade inversiva. A escolha desse hexacorde partiu da justaposição de dois tricordes que simultaneamente satisfizessem dois critérios: (1) ter uma relação de média-alta similaridade entre si, de acordo com decisão a priori mostrada na tabela 4; (2) produzir um hexacorde com combinatoriedade inversiva, de acordo com a tabela de hexacordes fornecida em Straus (2000, p. 221). Escolhemos [013] e [025] que têm similaridade 0,667, de acordo com a tabela 2 e, quando justapostos, geram o hexacorde 013469, que tem combinatoriedade inversiva. A partir desse hexacorde, construímos uma série dodecafônica (Figura 2) e sua matriz (Tabela 6).

Exemplo 1: Série dodecafônica do terceiro movimento.
O terceiro movimento (Fleumático) está estruturado em 4 seções nas quais são utilizadas as formas T3R, T7, T4I, T3I e T7RI. A primeira seção utiliza apenas a forma T3R (46731A520B98) e tem a extensão de 6 compassos. A seção seguinte, com 8 compassos é construída com as formas T7 e T4I que formam um agregado combinatorial inversivo. T7 é distribuída entre o violino 1 e a viola enquanto T4I aparece no violino 2 e no violoncello. Ainda na segunda seção os violinos apresentam T7 por completo antes de T4I reaparecer. A terceira seção apresenta T3I disposta numa textura simétrica especular com a primeira seção. Por fim, a quarta seção deste movimento é composta pelas formas T3R e T7RI (agregado combinatorial inversivo), T3R nos violinos e T7RI na viola e violoncello.
Tabela 6: Matriz dodecafônica para o terceiro movimento.
| 0 | 1 | 3 | 4 | 6 | 9 | 2 | 5 | 7 | 11 | 10 | 8 |
| 11 | 0 | 2 | 3 | 4 | 8 | 1 | 4 | 6 | 10 | 9 | 7 |
| 9 | 10 | 0 | 1 | 3 | 6 | 11 | 2 | 4 | 8 | 7 | 5 |
| 8 | 9 | 11 | 0 | 2 | 5 | 10 | 1 | 3 | 7 | 6 | 4 |
| 6 | 7 | 9 | 10 | 0 | 3 | 8 | 11 | 1 | 5 | 4 | 2 |
| 3 | 4 | 6 | 7 | 9 | 0 | 5 | 8 | 10 | 2 | 1 | 11 |
| 10 | 11 | 1 | 2 | 4 | 7 | 0 | 3 | 5 | 9 | 8 | 6 |
| 7 | 8 | 10 | 11 | 1 | 4 | 9 | 0 | 2 | 6 | 5 | 3 |
| 5 | 6 | 8 | 9 | 11 | 2 | 7 | 10 | 0 | 4 | 3 | 1 |
| 1 | 2 | 4 | 5 | 7 | 10 | 3 | 6 | 8 | 0 | 11 | 9 |
| 2 | 3 | 5 | 6 | 8 | 11 | 4 | 7 | 9 | 1 | 0 | 10 |
| 4 | 5 | 7 | 8 | 10 | 1 | 6 | 9 | 11 | 3 | 2 | 0 |
O quarto movimento (Colérico) é construído a partir do procedimento de multiplicação utilizado pelo compositor Pierre Boulez (STRAUS, 2000, p. 197-202). Colérico é dividido em 4 seções das quais 2 representam pequenos momentos de “contenção da cólera” e as outras representam momentos de cólera. Para cada uma dessas seções foi realizada uma multiplicação: para as seções de “contenção” multiplicou-se o tricorde principal [0, 1, 5] por dois tricordes com alta similaridade ([0, 1, 4] e [0, 1, 6], respectivamente); já para as seções de cólera multiplicou-se o tricorde [0, 1, 5] por [0, 2, 7] (retrogressão – classe A para classe D) e [0, 1, 5] por [0, 2, 5] (retrogressão – classe A para classe E). A melodia principal de cada seção é composta pela coleção de classes de notas resultante de cada operação, enquanto o acompanhamento é composto pelo complemento de cada resultado. Como houve um interesse em enfatizar a baixa similaridade (Tabela 4), é importante ressaltar que não foi feita nenhuma operação entre a classe A e a classe F, que é a classe com menor similaridade. Essa operação foi evitada na intenção de se obter maior diversidade do material utilizado, visto que o resultado dessa operação (0, 1, 3, 4, 5, 6, 7, 8, B) nos daria o próprio [0, 1, 5] (sob a forma de 29A) como complemento. Assim sendo, preferimos optar por utilizar a classe E para realizar a operação.
Dessa maneira, com o planejamento da obra Temperamentos, verificamos a aplicabilidade do nosso sistema, bem como, sua abertura a outros elementos não estabelecidos pelas definições iniciais. Nesse caso, tivemos a associação com a teoria dos humores corporais, de Hipócrates, como elemento extra-musical e, a intertextualidade com os procedimentos e sonoridades atribuídas a alguns importantes compositores do Século XX. A pri
meira página de Temperamentos é mostrada no Exemplo 2 abaixo.

Exemplo 2: Página inicial de Temperamentos.
Notas
As possibilidades combinatoriais desordenadas são calculadas pela Combinação de 12 elementos (escala
cromática) em subconjuntos com cardinalidade n, onde n varia de 0 a 12. Esse resultado é obtido pelo fatorial de 12 dividido pelo fatorial de n, o qual é multiplicado pelo fatorial de (12-n). Os resultados para todos os n (de 0 a 12) são somados, resultando no valor 4096 (na tabela abaixo, a soma de todas as colunas da segunda linha). Forte (1964, p. 145-148) inicialmente considera conjuntos de 2 até 10 elementos. Posteriormente (1973, p. 179-181), considera apenas conjuntos de 3 até 9 elementos, algo também adotado por Straus (2000, p. 221-224) e Roig-Francolí (2008, p. 362-365). Não abordaremos neste trabalho os Complexos de Conjuntos de Classes de Alturas (K, Kh) descritos por Allen Forte, na segunda parte de seu livro The Structure of Atonal Music.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C12,n | 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 |
2 O conceito de hierarquia é empregado aqui em seu sentido comum, ou seja, refere-se à organização de objetos em classes, numa ordem crescente ou decrescente, de acordo com certas propriedades definidas a priori. No nosso caso particular, essas propriedades são exclusivamente associadas à quantidade de classes de similaridade inerentes a cada tricorde.
3 Adotamos a definição de Benjamin Boretz (1970, p. 25): “sintaxe musical é essencialmente um modelo para a determinação da estrutura interligada de relações hierarquicamente conectadas, através do qual a gama de significações de um conjunto discriminável de dados podem ser interpretados”.
4 O terceiro movimento dos Cinco Movimentos para Quarteto de Cordas, Op.5, de Webern, por exemplo, apresenta, nos seis compassos iniciais, centricidade em Dó#. Como observa Straus (2000, p. 114), a centricidade na música pós-tonal pode ser estabelecida por alturas salientes, ou seja, alturas que são sustentadas substancialmente, que aparecem frequentemente, que são posicionadas nos registros extremos, acentuadas ritmicamente ou enfatizadas dinamicamente.
Referências bibliográficas
ANTOKOLETZ, Elliot. The Music of Béla Bartók. Los Angeles: University of California Press, 1984.
BERTALANFFY, Ludwig von. Teoria Geral dos Sistemas. Tradução: Francisco M. Guimarães. Petrópolis: Vozes, 2008.
BORETZ, Benjamin. The Construction of Musical Syntax I. Perscpectives of New Music, Vol. 1,
n. 1 (Autumn - Winter 1970): p. 23-42.
FORTE, Allen. A Theory of Set-Complexes for Music. Journal of Music Theory, Vol. 8, No. 2 (Winter, 1964), p. 136-183.
. The Structure of Atonal Music. New Haven: Yale University Press, 1973.
ISAACSON, Eric J. Similarity of Interval-Class Content between Pitch-Class Sets: The IcVSIM Relation. Journal of Music Theory, Vol. 34, No. 1 (Spring, 1990), p. 1-28.
LEWIN, D. A Response to a Response: on PCSet relatedness. Perspectives of New Music, Vol. 18, No. 1/2 (Autumn, 1979 – Summer, 1980), p. 498-502.
LIMA, Flávio. Desenvolvimento de Sistemas Composicionais a partir da Intertextualidade. Dissertação (Mestrado em Composição) – UFPB, João Pessoa, 2011.
McHOSE, Allen Irvine. The Contrapuntal Technique of the 18th Century. Englewood Cliffs, NJ: Prentice-Hall, 1947.
MENEZES, F. Apoteose de Schoenberg. São Paulo: Ateliê Editorial, 2002.
PEREIRA, Patrícia e GUZZO, Raquel. Diferenças Individuais: temperamento e personalidade (importância da teoria). Revista Estudos de Psicologia da PUC-Campinas. V. 19, n. 1 (janeiro/ abril de 2002): 91-100.
SMITH, Stuart, SMITH, Sylvia. A Portrait of Herbert Brun. Perspectives of New Music. Vol. 17. Nº 2 (Spring-Summer, 1979), p. 56-75.
ROIG-FRANCOLÍ, M. A. Understanding Atonal Music. Boston: McGraw-Hill, 2008.
STRAUS, Joseph N. Introduction to Post-Tonal Theory, 2a. Ed. Upper Saddle River: Prentice Hall, 2000.
WINHAM, Godfrey. Composition with Arrays. Perspectives of New Music. Vol. 9, Nº 1 (Autumn-Winter, 1970), p. 43-67.
Weskley Dantas - Estudante do Curso de Bacharelado em Composição Musical na Universidade Federal de Campina Grande (UFCG), onde estuda com Liduino Pitombeira. Tem produzido artigos na área de composição, um dos quais foi apresentado no XXI Congresso da ANPPOM, em Uberlândia.
Liduino Pitombeira - Sua música de tem sido executada pelo Quinteto de Sopros da Filarmônica de Berlim, Louisiana Sinfonietta, Orquestra Sinfônica do Recife (Brazil), Poznan Philharmonic Orchestra (Poland) e Orquestra Sinfonica do Estado de São Paulo (OSESP). Pitombeira recebeu seu PhD em composição pela Louisiana State University (EUA), onde estudou com Dinos Constantinides. Suas peças são publicadas pela Peters, Bella Musica, Criadores do Brasil (OSESP), Cantus Quercus, Conners, Alry, RioArte e Irmãos Vitale.