Grafos em Música

Desde que Leonhard Euler inaugurou a teoria dos Grafos em 1736 esta forma de modelagem matemática tem sido aplicada exaustivamente nas mais variadas áreas do conhecimento humano como lógica, ciências da computação, engenharia, filosofia, lingüística, biologia entre outras. Também a música faz parte dessa lista.¹ O conceito, em si, é muito simples e permanece o mesmo até hoje: construir diagramas compostos por vértices unidos por arestas. A este tipo de diagrama foi dada a denominação de Grafo. O objetivo deste trabalho é o de adaptar um tipo particular de grafo, conhecido como Dígrafo, para uso em música como forma de notação.

Exibiremos aqui os resultados de uma pesquisa no campo da representação escrita de música voltada para a elaboração de uma maneira formal, lógica, clara e inovadora de expressar progressões harmônicas. Os resultados podem ser interessantes para aqueles músicos que desejam visualizar, comunicar, entender e memorizar, de forma fácil e rápida, as informações harmônicas de uma dada música, ou mesmo de apenas um trecho de uma obra. Para tal, a nova notação trocou convenções do paradigma tradicional de escrita, como a leitura horizontal da esquerda para a direita (derivados da leitura de textos), por uma apresentação diagramática. Esta quebra de convenções, num primeiro momento pode dificultar ou intimidar a aprendizagem, mas pode também auxiliar num entendimento musical em seu caráter cíclico. Este novo modelo não se destina a todos os músicos, nem a todas as situações musicais, e não se propõe a substituir qualquer outra forma existente de representação. Está ligado a pratica de memorização, mentalização e improvisação de música através de seu encadear de acordes, o que já representa uma limitação auto-imposta ao sistema, mas também uma potencialidade de uso. Esta não é a prática em muitos ambientes musicais, mas é bem aceito, por exemplo, em MPB, jazz, e muitos outros estilos de música popular, especialmente entre executores de instrumentos ditos harmônicos (onde facilmente se pode tocar várias notas simultaneamente, como piano, guitarra e violão, por exemplo). Além de servir como leitura em performance, o modelo tem também potencial como ferramenta pedagógica para o ensino de harmonia, de percepção harmônica e iniciação musical, e ainda como interface homem-máquina para música eletrônica. Na última seção deste texto serão discutidas possíveis aplicações para esta representação.

O dígrafo aqui desenvolvido traz semelhanças com a modelagem de Autômatos Finitos que são também conhecidos pelo nome de máquina de estados e nos interessam especialmente pela relação que têm com o conceito de estados característicos. Neste tipo de modelagem, cada vértice do grafo representa um estado pelo qual se transita ao longo do tempo. Em música, estes estados serão caracterizados por acordes, e serão chamados Estados Musicais Harmônicos. Propõe-se, portanto, que obras musicais também possam ser descritas por fluxos de estados característicos. Músicas fluirão de estado para estado na medida que trocam de acorde e transitam entre funções tônicas, sub-dominantes e dominantes. O modelo aqui proposto será chamado Diagrama de Estados Musicais Harmônicos (DEMH).

Representações Conhecidas para Progressões Harmônicas

Em teoria musical, o estudo de progressões harmônicas tem se valido historicamente de diferentes notações escritas (CHEDIAK, 1986; HARTE, 2005; LA MOTTE, 1993; SCHOENBERG, 1911). O sucesso dessas notações esta relacionada, ao longo das épocas, com a importância dada pelos seus contemporâneos à informação harmônica para a criação de boa música, e na capacidade de instrumentistas em entender e utilizar essa notação, de alguma forma, em sua performance. A representação harmônica é, por assim dizer, inerentemente incompleta e generalizante. Incompleta por exigir considerável complementação do intérprete, que ainda precisa escolher que notas tocar a cada momento, e generalizante, por agrupar versões diferentes em uma mesma representação formal. Há algumas formas históricas de representação harmônica. O exemplo que não podemos deixar de citar é o do baixo cifrado, usado especialmente por instrumentos de basso continuo no contexto da música barroca. Um sistema que se valia de números associados a notas fundamentais para expressar acordes (Figura 1(a)).

No século XX, dois fatores contribuíram decisivamente para o desenvolvimento das notações harmônicas em uso atualmente: a aceitação da harmonia funcional (SCHOENBERG, 1953) e a grande disseminação da música popular. O primeiro ajudou a consolidar a maneira harmônica de entendimento musical entre estudiosos, a segunda popularizou a leitura de acordes entre musicistas amadores e profissionais.

Estes dois fenômenos se complementam e se contrapõem. O analista-erudito parte da música pronta, acabada e irretocável, e dela, ele extrai uma informação sintética a respeito do som. Precisa do sistema de cifras para usar no seu ponto de chegada: a sua análise. Já o músico leitor de cifras e o arranjador partem de uma música escrita ou pensada apenas de forma sintética, e disso adicionarão sua interpretação para a execução da música pronta nota por nota. O acorde é seu ponto de partida. É a análise anterior ao fenômeno. É a análise como causa. Ele não especifica comandos precisos de notas e interpretação, deixando muito em aberto, mas também sugerindo e delimitando um esquema de acompanhamento característico para obras musicais. É adicionando suas contribuições a partir deste ponto esquemático e diagramático que intérpretes se tornam também, em parte, compositores.

Os compositores, aliás, também fazem uso de cifras, mas de forma diferente aos personagens falados anteriormente. Para estes, a informação contida nas cifras pode ser tanto ponto de chegada quanto de partida. Estas cifras podem ser elemento de sua composição pronta e acabada (notar que, normalmente, uma linha melódica com cifras, por mais incompleto que seja, já dá conta de identificar quase qualquer música), como também pode ocorrer de um grupo de acordes ser a primeira semente que dá início a um longo processo composicional.

Por ser uma notação inerentemente resumida, a estratégia principal para o uso de cifras tem sido integrá-las com outras informações relacionadas às obras musicais como partitura, texto cantado e descrições textuais. Disso resultou uma série de convenções de uso, associadas a uma forma convencionada de nomenclatura de acordes. A esta nomenclatura se deu o nome de cifras. Embora esse sistema de nomenclatura nunca tenha conseguido se unificar totalmente, restando variações e redundâncias (HARTE, 2005), ele se tornou bem conhecido, e foi muito usado ao longo do século XX especialmente no campo da música popular e em análise musical.

Pesquisas atuais na área de representação harmônica estão freqüentemente ligados a questões de música computacional (BALABAN, 1996; DANNENBERG, 1993; HARTE, 2005; GRANDI, 2003; SCARBBOROUGH, 1989; SMITH, 1997; WIGGINS, 1993; WINOGRAD, 1968). Nestes, a interação com a máquina tem incentivado o surgimento de diferentes formas de representação e de dispor estas cifras para leitura (seja essa leitura realizada por homem ou máquina). Nesta área, como muitas vezes ocorre em artes, não foram impostas regras de antemão e até hoje não se viu um padrão prevalecer. Há várias possibilidades de disposição de informação harmônica. Em uma abordagem tradicional, as cifras são adicionadas a partituras melódicas, colocadas logo acima da pauta (Figura 1(b)), ou abaixo dela, ou então em compassos vazios de um sistema. Uma outra convenção encontrada em jazz posiciona cifras em uma partitura com apenas notação rítmica. Destina-se a músicos acompanhadores, e contém apenas informações harmônicas e rítmicas. Em outras notações mais informais vemos acordes sobrepostos a letras de canções, sem partitura (Figura 1(c)).

Figura 1: (a) Baixo cifrado. (b) Melodia com cifras. (c) Letra com cifras (d) Letra, cifras, compassos e analise (CHEDIAK, 1986, p. 257).

Também ocorre de a notação cifrada ser dada ao músico de forma desatrelada de letra e partitura, sendo deixado os acordes entre barras de compasso, ou simplesmente um depois do outro seqüencialmente. Outra notação põe os acordes em compassos (sem partitura melódica), mas inclui letra da canção e ainda o uso de setas e sinais gráficos para destacar algumas progressões especiais (Figura 1(d)). Esta forma de escrita esboça a introdução de elementos gráficos para dar destaque a cadências típicas, mas as setas se restringem a apontar os movimentos de resolução V – I e bII7 – I (conhecida também como SubV7 – I).

Observando estas alternativas logo se percebe que essas notações têm elementos em comum. Podemos, por exemplo, observar a reprodução de paradigmas da escrita textual. Em todos estes formatos a informação está organizada de certo modo sobre um eixo unidimensional, ou seja, em linhas lidas da esquerda para a direita. Tal não acontece na leitura de grafos.

O Dígrafo

O subtipo de grafo que nos interessa aqui é aquele cujas arestas são direcionadas, chamado Dígrafo. Na sua representação gráfica as arestas são setas, indicando vértice de saída e vértice de chegada, transmitindo uma idéia de fluxo entre vértices. Um Dígrafo é definido como um par ordenado

D: = (V, A) onde V é um conjunto de vértices v, e A é um conjunto de arestas a=(v1, v2) onde v1 e v2 são vértices que pertencem a V, e v1 é o vértice de saída e v2 é o vértice de chegada.

Vejamos um dígrafo (Figura 2) usado para modelar o funcionamento de uma simples porta com tranca.

D: = (V, A) V = {aberta, fechada, trancada} A = {(aberta, fechada), (fechada aberta), (fechada, trancada), (tran

cada, fechada)}

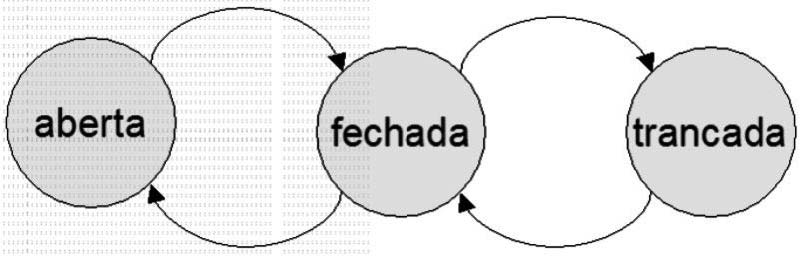
Figura 2: Dígrafo simples de uma porta com tranca.

O que é interessante notar neste exemplo é como cada vértice aqui representa um estado em que o objeto modelado se encontra. Além dos três estados, vemos as quatro transições (chamaremos as arestas do dígrafo de transição). Cada mudança de estado aqui é disparada por um evento aqui imprevisível de abrir porta, fechar, trancar e destrancar. Um estado é uma descrição momentânea do sistema. O modelo permite representar graficamente o comportamento do sistema ao exibir como este alterna entre os seus estados possíveis.

Alguns tipos mais sofisticados de dígrafo, como o Autômato Finito (KOZEN, 1997. HOPCROFT, 2001), acrescem a este modelo algumas características interessantes. Para o DEMH vamos incorporar a idéia de definir um estado inicial e um estado final e introduzir maneiras de tornar previsível a troca de estados, para que possamos fluir de modo controlado pelos estados musicais.

Descrição Formal

Nesta seção e nas próximas pretende-se discorrer formalmente sobre o modelo de Diagrama de estados harmônicos aqui proposto. A descrição formal do diagrama não é, possivelmente, a melhor forma de se ensinar o seu funcionamento, mas é necessária para uma fundamentação teórica rigorosa. Para manter controle sobre atualizações será empregado um sistema de numeração de versão. A versão apresentada aqui é a DEMH 2008.3.1.

Um Diagrama de Estados Musicais Harmônicos A usado para modelar uma progressão qualquer, é definido como sendo um conjunto ordenado contendo seis elementos.

Elementos do DEMH: O Conjunto Q de Estados Harmônicos

O estado harmônico expressa um certo intervalo de tempo durante a execução de uma música, no qual perdura uma certa inter-relação de sons que chamamos acorde. Graficamente o estado é representado por um disco colorido, ou em tom de cinza, com um acorde escrito em seu interior (em formato de cifra) e, se necessário, uma tonalidade indicada por um triângu-lo com ponta para baixo que chamaremos Sinal de Modulação (Figura 3). Matematicamente é descrito por um conjunto com dois elementos q = (k, t) onde k é um acorde simbolizado por sua cifra, ou seja, por um string de símbolos; e t é uma tonalidade, novamente um string de símbolos, e representa

o centro tonal da música quando naquele estado, ou seja, k dá a nota fundamental do acorde junto com sua configuração de acorde, e t a nota tônica da tonalidade, junto com informação de modo (maior, menor ou outro).

q1 = (Am, Lá menor)

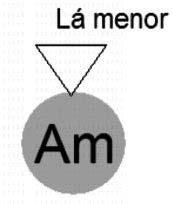
Figura 3: Exemplo de estado q1, com acorde Am e tonalidade Lá menor.

É importante notar que, no DEMH, estado e acorde são entidades ligadas, porém diferentes. Estados contém acordes (cada estado pode conter apenas um acorde) e estados diferentes podem conter o mesmo acorde, ou seja, dois estados qX e qY podem ter os mesmos elementos e continuarão sendo entidades diferentes. A escolha entre o uso de um mesmo estado em diferentes momentos da música, ou de estados diferentes com o mesmo acorde, será determinada caso-a-caso pelas características da música, e pela facilidade e conveniência da leitura.

Por fim, o conjunto total de estados expressos em um DEMH, incluindo estado inicial e estado final, constituirá o seu conjunto Q.

Elementos do DEMH: O Estado Inicial q0 e o Estado Final qf

É necessário ao DEMH definir, a priori e claramente, o estado inicial – de nome q0 – onde é iniciada a execução, e o estado final – de nome qf – onde a execução é encerrada (o DEMH admite apenas um único estado inicial e um único estado final). Ambos são definidos como estados q=(k,t), e pertencem ao conjunto Q de estados, porém têm acorde k e tonalidade t iguais a nulo. Graficamente estes são representados, respectivamente, por um disco preto pequeno e um disco preto pequeno com um circulo ao redor (Figura 4).

Figura 4: Estado inicial e estado final.

Pode-se dizer que o estado inicial é o estado em que a música se encontra antes de ser iniciada, e o estado final é o estado em que a música se encontra após o seu término. Um DEMH bem montado sempre será capaz de chegar ao estado final partindo do estado inicial.

Em muitas ocasiões, o DEMH é usado apenas para representar um trecho de uma música, e não a obra inteira. Quando o autor quiser destacar que seu diagrama representa uma seção de uma música, utiliza-se uma outra notação gráfica para estado inicial e estado final. O estado inicial se torna um quadrado preto, e o estado final é representado por um quadrado preto no centro de um quadrado branco (Figura 5). O nome do DEMH, ou seja, nome da seção representada por aquele diagrama, deve aparecer dentro de um retângulo sobre o estado inicial para ajudar em sua identificação. Este retângulo identificatório será conhecido como sinal de seção.

Figura 5: Notação para diagrama de seção.

Elementos do DEMH: O Conjunto T de Tonalidades t Usados pela Música

Para ajudar na leitura do DEMH em música tonal a tonalidade é explicitada graficamente. Esta notação prevê a possibilidade de modulação, portanto, um diagrama pode ter mais do que uma tonalidade, mudando de uma para outra ao longo de sua execução. Dessa forma a tonalidade estará expressa no início da música e, se for necessário, em cada estado onde houver modulação, ou seja, onde a tonalidade desse estado for diferente da tonalidade do estado anterior. Se a tonalidade aparecer apenas no início da música, o leitor assumirá que não ocorre modulação. Define-se T como um conjunto de tonalidades t, onde t é um string de símbolos que representa o nome da nota tônica e o modo associado usado (não importando o sistema de representação usado seja, por exemplo, Lá menor ou Am, sendo necessário apenas que não se troque de sistema num mesmo diagrama). Cada estado q em Q contem uma tonalidade t pertencente a T. Graficamente escreve-se o tom dentro ou junto a um triângulo com ponta virada para baixo, encostada ao estado em que se inicia esta nova tonalidade. Este triângulo receberá o nome de Sinal de Modulação (Figura 6).

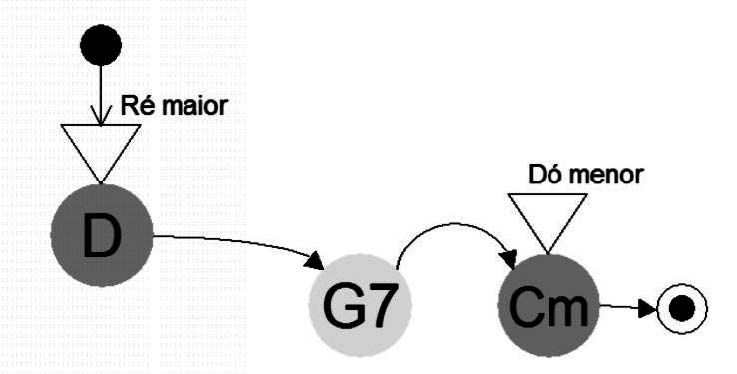
Figura 6: Progressão com dois Sinais de Modulação.

Opcionalmente a tonalidade inicial não precisa ser explicitada no DEMH se for descrita anteriormente de modo textual e não houver modulação, ou se o autor considerar, naquele contexto, desnecessário.

O DEMH pode ser adaptado também para música atonal, desde que a música em questão tenha estados harmônicos distinguíveis ou de alguma forma representáveis. Para isso basta definir T como conjunto vazio, o que afirmará que a música descrita não possui nenhum centro tonal.

Elementos do DEMH: O Conjunto de Acordes K

Podemos entender o conjunto K como sendo o conjunto de acordes a serem executadas pela música descrita pelo DEMH. Ou seja, K lista todos os acordes que uma música utilizará. Dessa maneira será constituída por um conjunto de nomes de acordes que obedeçam alguma convenção teórica consagrada pela teoria musical. Cada estado será rotulado pelo símbolo de acorde que ele contém. Qualquer sistema de representação pode ser adaptado. Não é objetivo deste presente artigo priorizar ou escolher algum sistema de notação harmônica. A simbologia a ser usada em cada estado fica a critério do autor que estiver usando o DEMH. O diagrama é, por princípio, adaptável.

Elementos do DEMH: O Conjunto ∆ de Transições

Uma transição ocorre quando, durante a execução de uma DEMH, acontece a troca entre um estado e outro. Uma passagem que ocorre de forma instantânea, sem consumo de tempo. Dessa maneira o sistema apresenta alteração de estado, ou seja, de maneira simples, a música troca de acorde.

As transições são representadas graficamente por setas que unem estados de forma a configurar um trajeto. São as arestas desse grafo. De modo formal define-se ∆ como o conjunto de transições δ = (q1, q2, p, N), onde q1 é chamado estado de saída, q2 é chamado estado de chegada, p é chamado passo e N é chamado ordem.

Os elementos q1 e q2 são estados diferentes entre si, pertencentes a Q que são conectados graficamente por uma seta que vai de q1 para q2. Passo é um número racional maior que zero, que denota quanto tempo o sistema ficará no estado de saída antes de acionar aquela transição e passar para o estado de chegada. Ordem é um conjunto de números inteiros. É usado em estados que são estado-de-saída em mais de uma transição (ou seja, estados com duas ou mais setas saindo) e é usado para definir qual das transições será acionada a cada vez que se chega nesse estado.

Pode-se dizer que o número de passo representa quantos compassos a música ficará naquele estado harmônico. No DEMH optou-se por exibir esse número de passo de maneira gráfica, ao invés de usar algarismos (Figura 7).

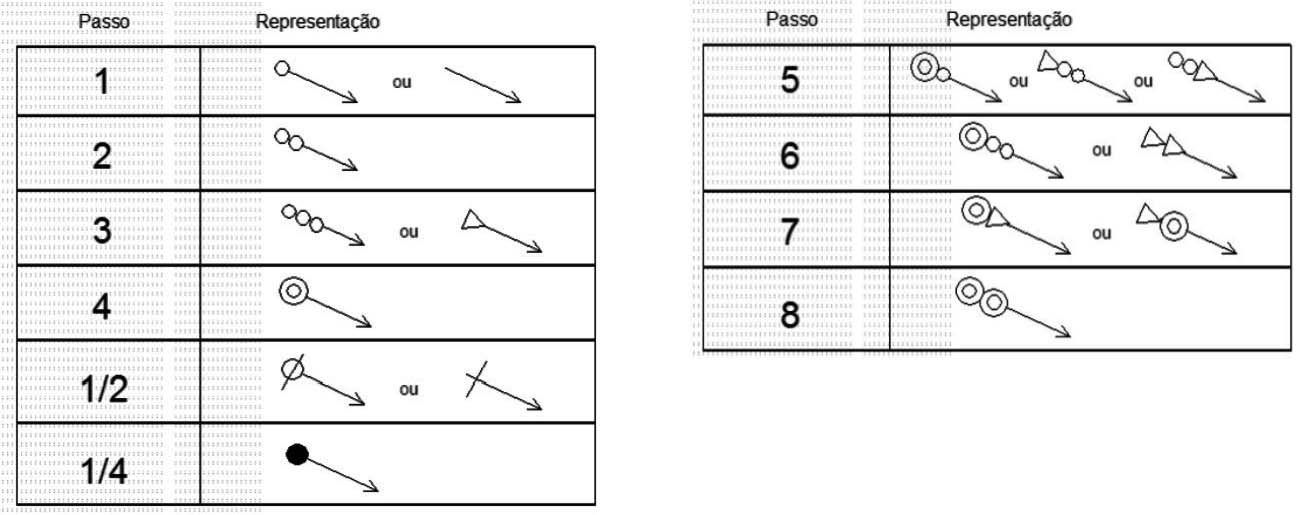
Figura 7: Representação de passo.

Por razões de leitura, no DEMH, podem ser usadas setas especiais que, além de denotar a transição, exprimem o intervalo de cadência entre um acorde e o seguinte (ou seja, o intervalo entre as notas fundamentais dos acordes da transição). Fazem isso representando distintamente cada possibilidade de cadência harmônica. É interessante notar que não é necessário expressar essa informação matematicamente na formulação de uma transição visto que, uma vez que se tenha os acordes, a cadência entre eles é informação dedutível e redundante.

Visto que há doze notas cromáticas, há, portanto, doze diferentes intervalos de cadência possíveis. Onze com deslocamento da nota fundamental, e a progressão sem deslocamento de fundamental (por exemplo a progressão de C para Cm). De início vamos classificar os intervalos de cadências em apenas quatro tipos: Segundas, Terças, Quartas e as sem alteração de nota fundamental que chamaremos Isofundamentais. As cadências de segunda sendo representadas por uma linha dupla, as de terça por linhas triplas, as de quarta por linha simples (exatamente por ser a transição mais comum) e a isofundamental representada pela ausência de linha, simplesmente encostando-se um estado no seguinte. Visto que o intervalo de quinta é também uma quarta, só que descendente (invertida), elas podem ser representadas com um tipo semelhante de seta. Também a sexta é uma terça invertida, e a sétima uma segunda invertida. Diferenciaremos estas cadências invertidas apenas por um símbolo que representará a inversão do intervalo de cadência: a ponta da seta – Branca, no caso de apresentar inversão, e Preta quando não. Agora basta incluirmos uma maneira de representar os respectivos intervalos menores e diminuídos (adicionando um bemol sobre a transição) de segunda menor, terça menor, quinta diminuída, sexta menor e sétima menor, e temos uma simbologia que cobre todas as 12 possibilidades de cadência (Figura 8).

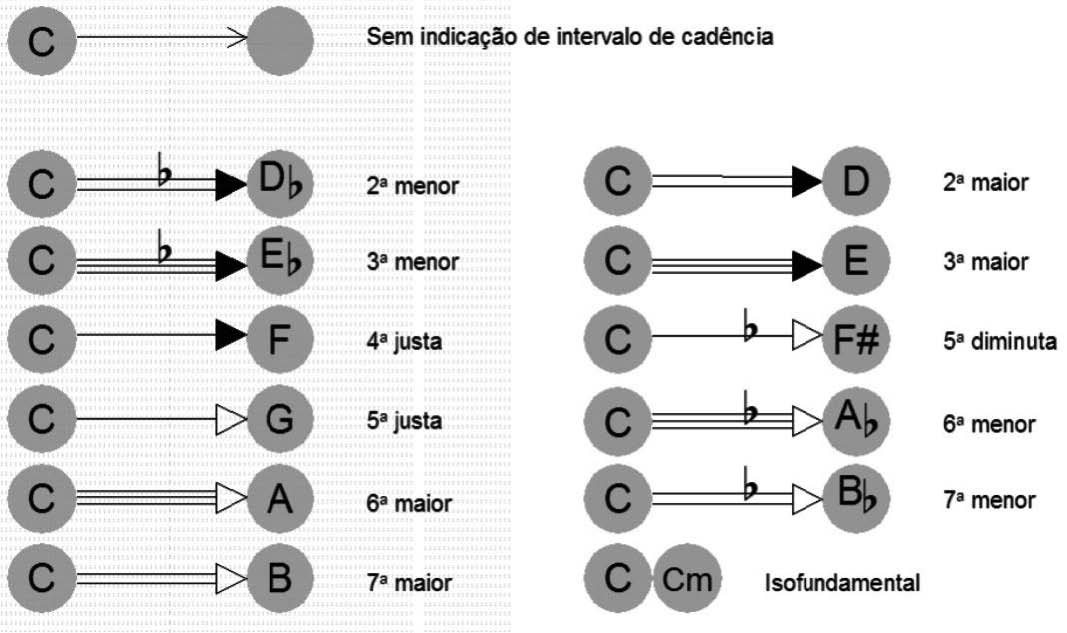
Figura 8: Representação de Transições de acordo com o intervalo de cadência.

Como foi mencionado, haverá estados com várias possíveis transições de saída. Para que a execução saiba qual transição seguir, em estados desse tipo, cada transição será ordenada. Para se determinar essa ordem, cada transição possui um conjunto de números naturais chamado Ordem. A cada vez que o leitor chegar a um estado, escolherá a transição de saída que possuir no seu conjunto Ordem, o número igual ao número de vezes em que se chegou nesse estado na presente execução. Ou seja, na primeira vez que chegar a este estado, escolherá a transição de saída que contém o número 1 no seu conjunto ordem, na segunda vez a com número 2 e assim por diante. Se a execução chegar a um estado pela n-ésima vez, e o número n não estiver presente em nenhuma das transições saindo deste estado, retorna-se a contagem para um.

No caso de transições cujo estado de saída não é estado de saída de nenhuma outra transição (estados com apenas uma transição saindo), a ordem é um conjunto com apenas o número 1.

No diagrama, este conjunto de um ou mais números, aparecerá junto às transições apenas nos estados com mais de uma transição saindo. Pode-se ainda optar por não exibir estes números. No caso de um diagrama não mostrar números de ordem, o leitor entenderá que se deve escolher a transição de saída seguindo a ordem horária a partir da transição de chegada.

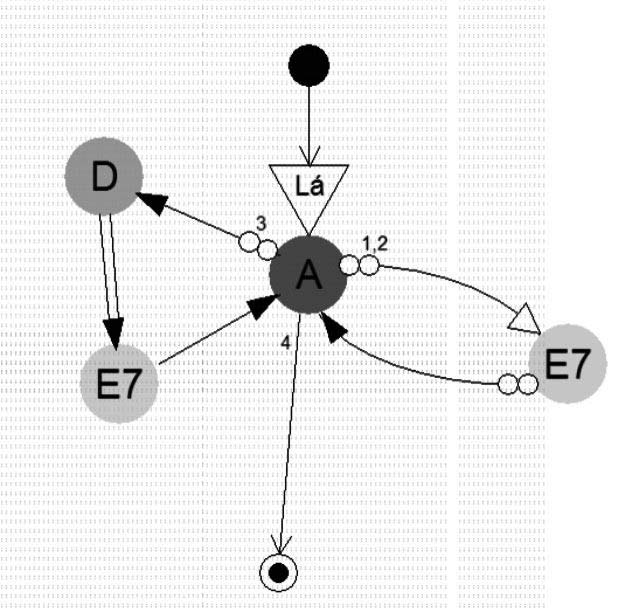
No exemplo da Figura 9 temos um DEMH de nome D1.

D1: = (Q, q0, qf, K, T, ∆)

Q = {q0, q1, q2, q3, q4, qf} onde q1 = (A, Lá) q2 = (E7, Lá) q3 = (D, Lá) q4 = (E7, Lá)

K = {A, E7, D} T = {Lá} ∆ = {δ1 = (q0, q1, 1, {1}),

δ2 = (q1, q2, 2,{1,2}), δ3 = (q2, q1, 2, {1}), δ4 = (q1, q3, 2, {3}), δ5 = (q3, q4, 1, {1}), δ6 = (q4, q1, 1, {1}), δ7 = (q1, qf, 1, {4})}

Figura 9: O Diagrama de Estados Musicais Harmônicos D1.

Informação Funcional

Estados podem ainda ser identificados visualmente com alguma função harmônica (tônica, sub-dominante e dominante) alterando se a cor ou tom de cinza do estado. Utilizaremos a proposta monocromática representada na Figura 10.

Por convenção os estados com acordes de função tônica (denominados Estados Tônicos) serão de cor ou escala de cinza mais escura, ou preto. O Dominante ficando com escala de cinza mais clara e o sub-dominante em posição intermediária, como ilustrado. Como recurso adicional, pode-se representar dominantes secundários ou sub-dominantes secundários (acordes cuja relação funcional é com um acorde de chegada diferente do acorde tônico, como, por exemplo, o II7 que é dominante da dominante) pela transformação do disco em rosca como ilustrado.

A função harmônica de um estado, em um DEMH, constitui informação matematicamente redundante uma vez que se sabe os acordes. É, por isso, considerado um recurso opcional do DEMH, porém se trata de um recurso com grande apelo visual cujo uso é recomendável.

Sinal de Salto

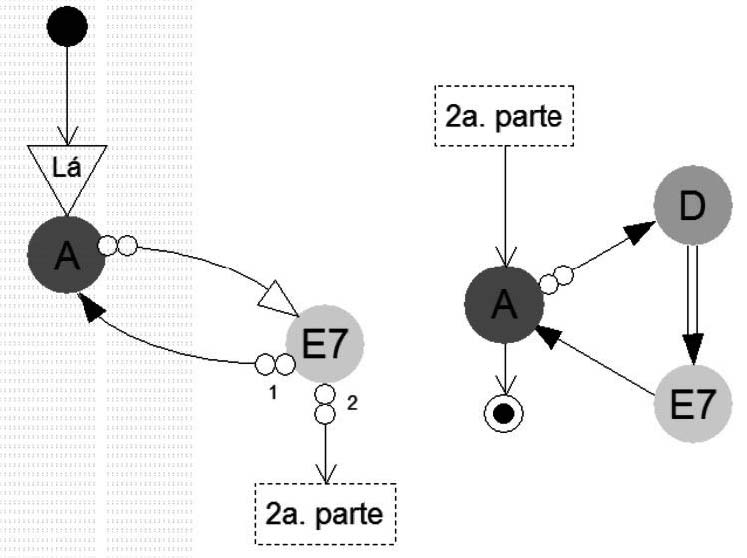
Um DEMH pode ser secionado utilizando o sinal de salto, representado por um retângulo tracejado contendo um símbolo de identificação qualquer. Estes sinais não aparecem na formulação matemática do DEMH e existem apenas para facilitar a leitura e entendimento do diagrama. O sinal de salto pode “quebrar” a representação gráfica de uma transição, permitindo que sua continuação seja colocada em qualquer outro lugar do espaço de apresentação. Esse recurso tem por função ajudar a organizar e analisar as cadências harmônicas destacando trechos nomeáveis. O DEMH no diagrama da Figura 11, é equivalente ao da Figura 9 usado em nosso exemplo D1, embora sua representação gráfica seja diferente. É dito equivalente, pois execuções de ambos os diagramas terão resultados iguais, ou seja, os mesmos acordes serão tocados nos mesmos intervalos de tempo, mas não são idênticos, pois no DEMH da Figura 11 temos um estado a mais e uma transição a mais. Essas alterações foram causadas pela quebra do estado q1 em dois estados, o que permitiu a inserção de um salto na transição δ4 e a separação do diagrama em dois segmentos. O símbolo de identificação do salto aqui usado é “2a. parte”.

D2: = (Q, q0, qf, K, T, ∆)

Q = {q0, q1, q2, q3, q4, q5, qf} onde

q1 = (A, Lá)

q2 = (E7, Lá)

q3 = (D, Lá)

q4 = (E7, Lá)

q5 = (A, Lá) K = {A, E7, D}

T = {Lá}

∆ = {δ1 = (q0, q1, 1, {1}), δ2 = (q1, q2, 2, {1}), δ3 = (q2, q1, 2, {1}), δ4 = (q2, q5, 2, {2}), δ5 = (q5, q3, 2, {1}), δ6 = (q3, q4, 1, {1}), δ7 = (q4, q5, 1, {1}), δ8 = (q5, qf, 1, {2})}

Figura 11: O Diagrama de Estados Musicais Harmônicos D2.

Símbolos Especiais

Muitos outros símbolos podem ser livremente incorporados aos diagramas desde que sua presença não crie confusão ou atrapalhe a leitura dos outros símbolos do diagrama.

Muitos sinais podem ser importados da notação clássica sem muitos problemas, como sinais de expressão (f, pp, >, etc.) por exemplo. Um outro acréscimo interessante são os sinais de métrica da música. Por exemplo representação de compasso quaternário, binário, etc. Sinais para convenções rítmicas também são representáveis. Há todo um campo de possibilidades a ser explorada. Todos os símbolos que não são parte da formulação matemática do DEMH, mas que são inseridos no diagrama, serão chamados símbolos especiais.

Todos esses símbolos podem ser inseridos no diagrama como informação visual, mas muitos podem não ser realmente interpretáveis. Mesmo metaforicamente. O ritornelo, por exemplo, perde muito do seu sentido num Dígrafo. Nem tudo é cabível, mas em última análise não há nada que impeça a inserção de pedaços de partitura, texto e imagens junto a um diagrama.

Exemplos Práticos de Diagramas DEMH

Nesta seção vamos mostrar dois exemplos práticos de diagramas DEMH.

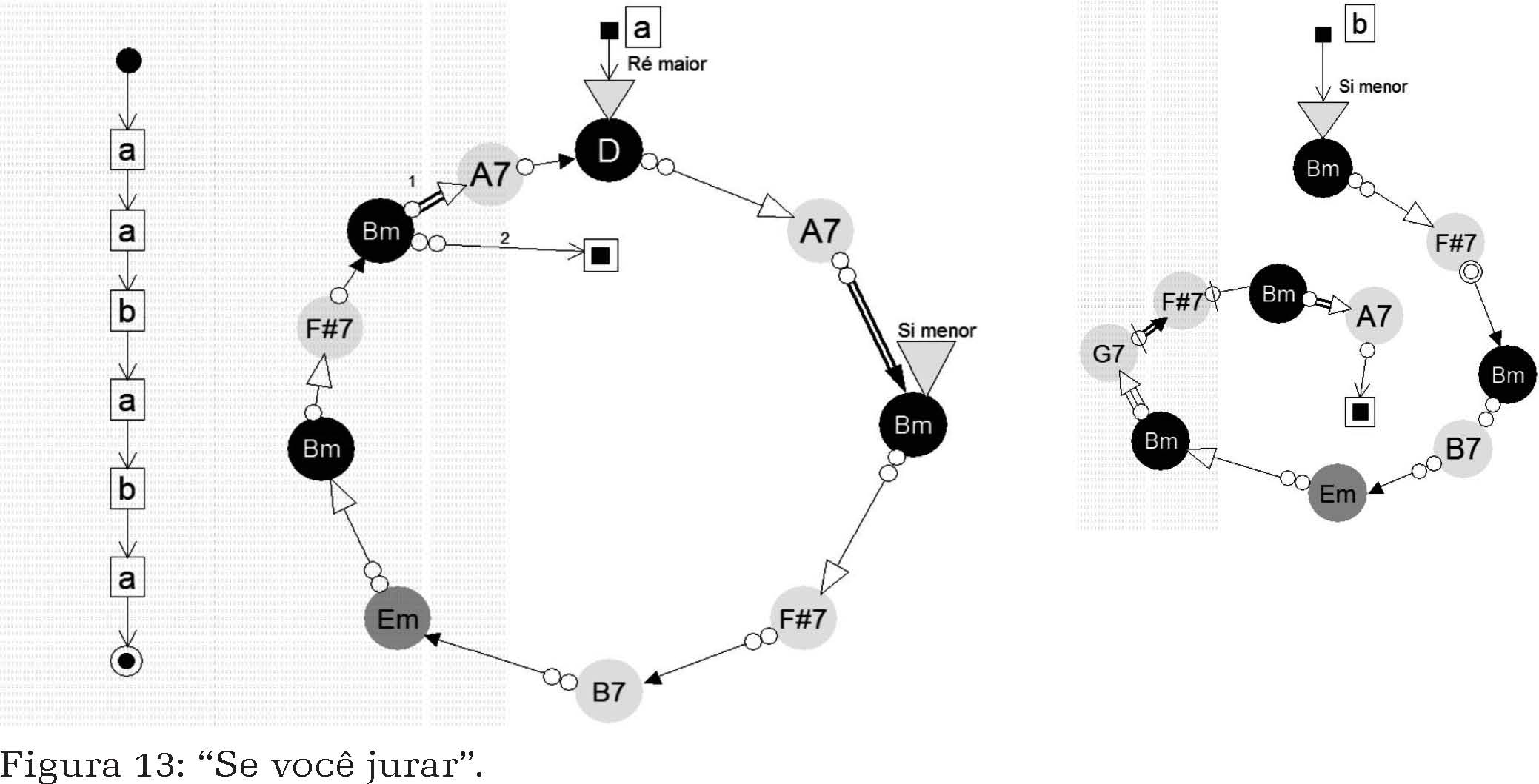
A canção “Vamos Fugir” de Gilberto Gil (Figura 12), e a canção “Se você jurar”, de Ismael Silva, Nilton Bastos e Francisco Alves, de 1931 (Figura 13).

Vamos Fugir:

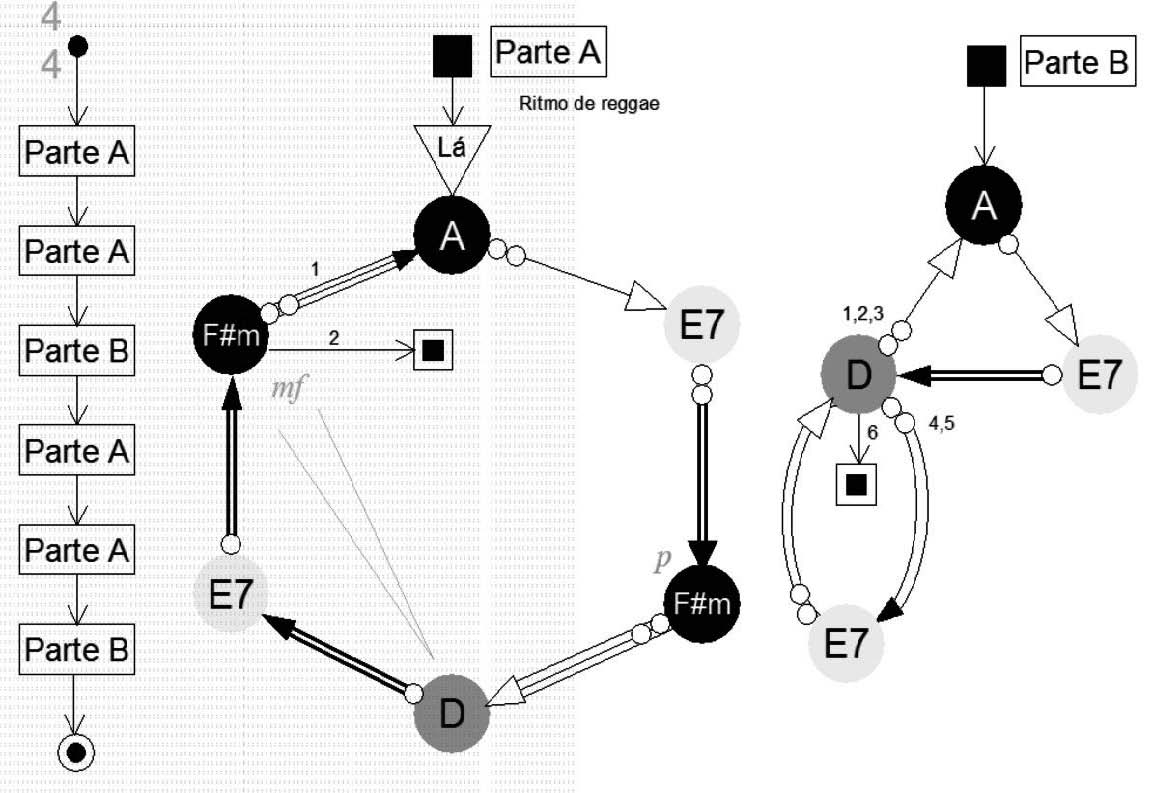
Integração com Escritas Tradicionais

Uma questão muito importante é a integração com outras formas de escrita, em particular, o texto escrito e a partitura. Não é o propósito desta nova notação se isolar de todas estas outras poderosas ferramentas representacionais. Pelo contrário, o intuito é que se busque meios para integrar estas escritas para que atuem juntas.

Há duas principais estratégias: que se leve o diagrama até a notação tradicional ou que se leve a notação tradicional para o diagrama.

No primeiro caso a abordagem é trazer o diagrama para dentro do paradigma de leitura de textos. Organizar em linhas lidas da esquerda para a direita, ordenados de cima pra baixo, como muitos estão acostumados. Dessa maneira adiciona-se o diagrama a partituras e textos, correndo em paralelo. O diagrama se torna linear e cursivo (Figura 14). Perde em ciclicidade, mas pode ser interessante em alguns contextos.

A outra estratégia possível é trazer mais e mais elementos de outras notações para dentro do DEMH usando os símbolos especiais.

Uso e Aplicações

Como ferramenta que auxilia na expressão de progressões harmônicas, foram identificadas duas principais aplicações para o DEMH. 1) Escrita musical com fins de execução e análise musical. 2) Ferramenta pedagógica para ensino de harmonia, percepção e iniciação musical.

Como escrita musical, atende qualquer músico que faz uso de informação harmônica de alguma forma. Serve para registro e transmissão, e é mais um possível canal de comunicação entre autores e intérpretes. É também uma ferramenta a mais de análise, trazendo de interessante não alguma nova teoria, mas simplesmente uma forma compreensiva e inovadora de representação visual. Esta maneira diagramática de se exibir informação harmônica permite uma visualização gráfica bidimensional da estrutura da música, podendo incentivar novas possibilidades de entendimento. Pode ser aplicado, portanto, em performance (seja como formato principal da escrita, ou técnica acessória) e em material bibliográfico.

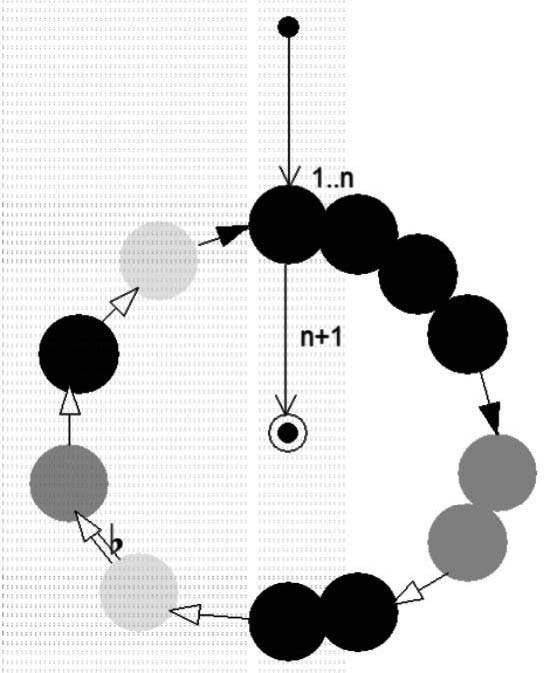
Como ferramenta pedagógica, o diagrama pode auxiliar como mais um meio no ensino da teoria da harmonia musical, percepção, e em iniciação musical. Pode ser empregado em sala de aula, em livros pedagógicos, ou em outro contexto como o áudio-visual, por exemplo. É uma representação escrita adaptável que realiza um interessante cruzamento entre informação sonora e uma informação visual, gráfica, simbólica, não textual. Na Figura 15 está ilustrado como o DEMH pode ser adaptado para falar-se de alguma progressão em especial – neste caso um ciclo de Blues ligeiramente alterado

– sem que haja necessidade de se lançar mão de formalismos musicais, partituras, nomes de acordes, cifras, ou outra convenção da teoria musical.

Além das aplicações citadas, este diagrama tem potencial para ser usado como um sistema de interface homem-máquina em aparelhagens automatizados de música eletrônica. É possível que, futuramente, seja desenvolvido um dispositivo que permita manipular um DEMH eletronicamente, de modo que este diagrama controle algum sistema de execução sonora capaz de interpretar informação harmônica.

Conclusões

Este artigo apresentou a versão 2008.3.1. deste modelo. Como a própria numeração sugere o DEMH não é considerado pronto e acabado. Ao contrário, esta é a primeira versão publicada deste diagrama, e há muito por fazer. Atualmente, a frente de desenvolvimento mais importante para este projeto é a implementação de um software específico para sua escrita² o que permitirá futuramente a rápida elaboração e edição de diagramas. Ademais também se estuda formas eficientes de integrar letras de canções e diversos elementos da notação musical tradicional dentro do grafo DEMH e está sendo planejado alguma forma de avaliação experimental deste modelo.

Notas

¹ Há muitas aplicações pouco conhecidas de grafos em música. Apenas para citar alguns exemplos, grafos podem ser vistos sendo usados em sistemas automáticos para compor música (TREVINO-RODRIGUES, 2001), para algoritmos de reconhecimento de símbolos musicais em papel, para o estudo das relações entre acordes (chordal spaces), para organizar esses acordes em um tipo de dicionário (GRANDI, 2003), para elaborar automaticamente setlists musicais (PINTO, 2007), e até num programa de computador engenhoso feito para calcular o dedilhado de violão ideal a partir de uma dada partitura (trabalho de graduação em computação da UFPE feito por Alexandre Sarmento Alves de Sá Extração de Conhecimento Musical a partir de Execuções Violonísticas. 2006. Não publicado). De maneira geral percebe se que a maioria das aplicações de grafos em música envolve também algum uso de informática.

² Todos os diagramas mostrados aqui neste artigo foram feitos manualmente no programa MS PowerPoint, ou seja, um software de uso geral, e, durante esse processo, foi constatada a necessidade de uma ferramenta gráfica específica. Devido a toda a sua complexidade de escrita, a implementação de um software aberto de interface amigável voltado para a tarefa de desenhar DEMHs é indispensável para o desenvolvimento futuro dessa notação.

Referências:

BALABAN, Mira. The Music Structures Approach to Knowledge Representation for Music Processing. Computer Music Journal, Boston, v. 20, n. 2, p. 96-111, 1996.

CHEDIAK, Almir. Harmonia e Improvisação. Rio de Janeiro: Lumiar, 1986.

DANNENBERG, Roger B. Music Representation Issues, Techniques, and Systems, Computer Music Journal, Boston, v. 17, n. 3, p. 20-30, 1993.

GRANDI, R. H.; COSTALONGA, L. L.; MENEZES, P. F. B.; VICCARI, R. M. Utilização do Ambiente Astrha para Implementar um Dicionário de Acordes Baseado em Autômatos Finitos. In: SIMPÓSIO BRASILEIRO EM COMPUTAÇÃO MUSICAL, 9, Campinas, SP, Anais do..., 2003.

HARTE, Cristopher; SANDLER, Mark; Emilia GÓMEZ. Symbolic representation of musical chords: A proposed syntax for text annotations. 6^th INTERNATIONAL CONFERENCE ON MUSIC INFORMATION RETRIEVEL London, 2005.

HOPCROFT, John E. Introduction to Automata Theory, Languages and Computation. Boston: Addison-Wesley, 2001.

KOZEN, Dexter L. Automata and Computability. New York: Springer-Verlag, 1997.

LA MOTTE, D. Armonia. Barcelona: Labor, 1993.

PINTO, A; VAN LEUKEN, R.; DEMIRCI, F., WIERING, F.; VELTKAMP, RC. Indexing music collections through graph spectra. 8^th INTERNATIONAL CONFERENCE ON MUSIC INFORMATION RETRIEVEL, Vienna. 2007.

SCARBOROUGH, Don L.; MILLER, Ben O.; JONES, Jacqueline A. Connectionist Models for Tonal Analysis, Computaer Music Journal, Boston, v. 13, n. 3, p. 49-55, 1989.

SCHOENBERG, Arnold. Harmonia. Tradução de Marden Maluf, São Paulo: Editora da Unesp, 1999 [1911].

SCHOENBERG, Arnold. Structural Functions of Harmony. New York: W.W. Norton, 1953.

SMITH, Sean M.; WILLIAMS, Glen N. A Visualization of Music, 8^th CONFERENCE OF VISUALIZATION, Phoenix - Arizona, v. 24, Issue 24, p. 499-503, 1997.

TRIVINO-RODRIGUEZ, J. L., MORALES-BUENO, R. Using Multiattribute Prediction Suffix Graphs to Predict and Generate Music, Computer Music Journal, Boston,

v. 25, n. 3, 2001.

WIGGINS, Geraint; MIRANDA, Eduardo; SMAILL, Alan; HARRIS, Mitch. A Framework for the Evaluation of Music Representation Systems, Computer Music Journal, Boston, v. 17, n. 3, p. 31-42, 1993.

WINOGRAD, Terry. Linguistics and the Computer Analysis of Tonal Harmony, Computer Music Journal, Boston, v. 12, n. 1, p. 2-49, 1968.

Alexei Queiroz - Aluno do curso de mestrado em música da UNICAMP, onde está redigindo uma dissertação na área de Educação Musical. Fez Bacharelado em Música Popular nessa mesma universidade e anteriormente já havia se graduado analista de sistemas em Ciências da Computação pela Universidade Federal de Santa Catarina. É compositor, cantor, músico, desenhista e escritor. Vem oferecendo aulas de Canto e Musicalização para adultos e crianças desde 2004.